Towards more meaningful math notation

By Murray Bourne, 11 Jun 2007

Students struggle a lot with the way mathematics is written.

For example, most students don't have too much of a problem with:

5(a + b) = 5a + 5b

Then they see this and it is also OK:

5(ab) = 5ab

In most cases you can substitute various values of a and b and the students can see that it works. Fair enough. Then the student does twenty (mind-numbing) examples of such bracket expansion and they feel they have got it.

Later, they come across things like:

sin(a + b)

And then their math teacher goes ape when the student expands it like:

sin(a + b) = sin a + sin b

Perfectly logical, in the minds of the student.

Similarly, it is logical to have the following, isn't it?

log(a + b) = log a + log b

Oh, and then we have functions. You know, like this:

f(x)

Is that the same as

f × x? (That is, f multiplied by x?)

Why not?

I wish to propose an alternative notation for concepts where you cannot expand in the way you do with simple algebra. It might look something like this:

Log

sine

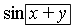
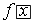
function

This would send a much clearer message to students that the particular function or operation does not work in the same way as simple algebra works.

Now, the proposed rectangle would be a nightmare given that we need to type mathematics (actually, everything is a nightmare when you are trying to type mathematics...).

So a more computer friendly option would be to (exclusively) use [ ] - square brackets - for such concepts, like this:

sin[x + y]

log[x + y]

f[x]

Would this work? Would it confuse everyone even more? I feel that if such a notation were to be universally adopted, then less confusion would arise.

[I wrote about notation before in Phase shift or Phase Angle?].

See the 66 Comments below.

Posted in Learning mathematics category - 11 Jun 2007 [Permalink]

Tags: Math notation, Technology

66 Comments on “Towards more meaningful math notation”

Dan Greene says:
11 Jun 2007 at 5:28 pm [Comment permalink]
Hi Zac,

As a math teacher, I agree with what you are saying. We have quite a few confusing notations that are conventionally used, but could be changed. Add to your (parentheses as function) vs. (parentheses as multiplication) problem the negative sign... 1) opposite of a number 2) subtract a number 3)as an exponenent, take the reciprocal of the base 4) f^-1(x), take the inverse of the function.

And of course, logs, which I wrote about on my site.

I doubt notations will change any time soon. I guess the best thing we can do right now is to recognize it as a problem and provid students with explicit instruction about avoiding these pitfalls.
Murray says:
12 Jun 2007 at 6:57 am [Comment permalink]
Dan - thanks for your comment.

I fully agree with your point about raising to the power -1.

In my math site, I use "arcsin" and "arccos" etc for the inverse trigonometric functions. For example, see Trigonometric Functions of any Angle, where it says:
NOTE: Why do I use "arcsin" instead of what is on your calculator, "sin^-1"?
- Students always get confused with sin^-1x and csc x (they are NOT the same: sin^-1x means "the angle whose sine is x", whereas csc x means "1/sin x").
- It is standard in science and engineering to use "arcsin".
- Most computer programs use "arcsin" or "asin" for the inverse of sine - not "sin^-1", so it is good practice to get used to it.
uliang says:
12 Jun 2007 at 12:39 pm [Comment permalink]
Hi,

I read your post with interest. I'm a graduate student in mathematics.

Indeed the mathematics computer software program Mathematica(TM) uses the square bracket notation for functions i.e. log(x+y) must be written as Log[x+y] with its syntax.

However, for later use, the round bracket notation is still be best(quickest) and easiest to use, esp in higher level maths, e.g. A-levels or engineering use. To a first timer it may be hard to get used to at first, but after repeated correction and usage, one can distinguish between a(b)=a.b and a(b) as a function.
Murray says:
12 Jun 2007 at 12:46 pm [Comment permalink]
Thanks, Uliang for your thoughts.

Yes, you are now used to it and so am I - but we have been dealing with higher level mathematics for some time. But there are thousands (millions?) of students who are clueless because of bad notation. They never get to see higher mathematics because they are so confused by something that is unnecessarily inconsistent.

Why is English so difficult to learn for non-native speakers? Because it is full of inconsistencies in spelling and grammar. Math has the same problems.

I'm just wondering - why do you feel that round brackets are quicker and easier? I would argue that the time taken to write ( ) and [ ] and { }, for that matter, are all much the same. But if their meaning was more intelligently applied, we would spend a lot less time in secondary school maths classrooms trying to explain why things work one way here and another way there, even though they look the same.

Heck, some students may even hate mathematics less, and decide to continue studying it!
Brent says:
15 Jun 2007 at 6:40 pm [Comment permalink]
This is a brilliant idea. When I was teaching high school I would also see students with an equation like cos(x) = blah try to "divide by cos"... which of course doesn't make any sense, but by analogy with 5(x) = blah it makes a lot of sense. I'd never really thought clearly about the problem with notation before.

I think it's entirely feasible to teach kids the bracket notation, and then inform them later that most people just write parentheses -- by that point I don't think it would be too hard for students to transition to always *writing* parentheses but *thinking* brackets in their head.
Steven says:
16 Jun 2007 at 5:10 am [Comment permalink]
What about calculus?

There are several ways of writing differentiation, and they mostly mean the same thing:

dy/dx
y'
f'
f'(x)
x dot (I mean x with a dot above, meaning dx/dt)

Surely this notation needs tidying up, too?
Murray says:
16 Jun 2007 at 4:13 am [Comment permalink]
Thanks, Brent for your comment.

I was suggesting a permanent change, but you have a good point. Perhaps students could start with square bracket notation and move on to the plethora of existing notations later.
Murray says:
16 Jun 2007 at 6:02 am [Comment permalink]
I agree, Steven.

When students start differentiation, they are nearly always dragged through "first principles".

The notation is usually horrendous:

lim Δx → 0 {(f(x + Δx) − f(x))/Δx}

Say what? Not only do the students have to cope with a challenging new concept ("gets closer and closer to but doesn't actually get there"), but a horrible notation.

I have used "h" instead of Δx in the section in the math site: Derivative by First Principles.
David Speyer says:
17 Jun 2007 at 12:08 pm [Comment permalink]
By the way, this is Mathematica's notation. "()" indicates order of operations, "[]" indicates application of functions, "{}" indicates an ordered pair or a list. So

ParametricPlot[{Sin[t], 2*(Cos[t]+1)}]

would plot an ellipse whose x-coordinate is Sin[t] and whose y-coordinate is 2*(Cos[t]+1). (Also, "[[]]" indexes into a vector or array, but pedagogically we want to discourage students from thinking of an array and a function as different objects.)

I find that I have very little trouble making these distinctions, even when I've been away from the software for several months, so I think it would be easy for experienced mathematicians to switch to the new notation.
Joshua Green says:
19 Jun 2007 at 12:30 am [Comment permalink]
This is an interesting idea that could also help students keep the concepts of "function" and "argument" clearer. On the other hand, I feel that if we were more consistent with function notation, we may not need such changes. My personal pet peeve is with the notations used for the trig functions. In general, for a function ƒ and its argument x, we write the value as ƒ(x). But for the function sine we often just write sin x. Worse, ƒ2(x) usually means ƒ(ƒ(x)), but sin2(x) means [sin(x)]2, and then it's not at all clear what sin-1(x) should mean.
Rika says:
20 Jun 2007 at 2:48 pm [Comment permalink]
I live and teach Mathematics in South Africa, and I am so glad to here that maths teachers elsewhere have the same problems as I have. A brilliant idea, to change the notation.
Murray says:
21 Jun 2007 at 12:57 am [Comment permalink]
Hi Rika and thanks for your comment. Math students seem to face the same algebra, trigonometry and logarithm problems world-wide, and I am sure notation is a big part of the mystery - and it need not be so.
jk says:
22 Jun 2007 at 11:29 am [Comment permalink]
I'm not convinced about the need for a change. If you like, you can think of the notation 5(.) as representing the function "multiply-by-5". OK, that's not how you would think about it when learning multiplication (or teaching it), but the point is that one can make it consistent. In any case, I don't see how changing the notation helps. Even thinking purely in terms of functions, we know there are functions for which f(x+y)=f(x)+f(y), and other functions where this does not hold, so why would the confusion go away by changing to brackets instead of parentheses?
Murray says:
22 Jun 2007 at 1:36 pm [Comment permalink]
You're right, jk about functions of the form f(x+y)=f(x)+f(y).

What I am suggesting is more like a "flag" to indicate to novice users that a particular item will most likely behave differently to some other item.

I'm still thinking about how you could ever make "5(.)" consistent with any of the existing inconsistencies in math notation...
Jacob says:
15 Jul 2007 at 3:44 am [Comment permalink]
this may make things easier at the beginning, but eventually if the student starts using generic operators, this could lead to confusion, as some are linear and some aren't. I think it may be better to always use x*(a+b) in cases where there is likely to be confusion with multiplication, and stress the difference when functions/operators are introduced, rather than to change the function notation.
Alexey Romanov says:
24 Oct 2007 at 7:38 pm [Comment permalink]
It seems better to simply use multiplication sign. Reserve juxtaposition for function application.
Murray says:
25 Oct 2007 at 11:51 am [Comment permalink]
That sounds like a good compromise to me, Alexey.
Magick says:
17 Jan 2008 at 7:11 am [Comment permalink]
I think this is such a great topic, so I'm going to bring it up again. It seems like much of these notations came about just to save memory on devices such as graphing calculators. Luckily, I know most of the rules and exceptions, so I never really have problems with this. I have noticed fellow classmates having problems, though. I have used websites which use brackets for functions and parentheses for order of operations; I thought it was a good idea. So, I do agree that there should be a standardized set of math notations.

Unfortunately, this is very similar to the English standard versus the Metric system. I'm sure we can all agree that there is practically no advantage in using standard measurements. This changes nothing, though. The entire nation is still stuck with this terrible system and is barely doing anything to change it.

I would love for these changes to happen (adopting the Metric system and creating a better system of math notations), but I doubt I will see that day.
Murray says:
17 Jan 2008 at 11:05 am [Comment permalink]
Hi Magick and thanks for your response.

I’m a little confused by this statement: "I’m sure we can all agree that there is practically no advantage in using standard measurements."

The rest of your statement appears to contradict this.

A quick story for you. In the early 1970s, Australia bit the bullet and required, by law, the conversion to the metric system. There was grumbling and some inconvenience for a while, but it happened. And it made life much easier for math students and their teachers.

Schools had been teaching both systems during the 60s and then only metric in the 70s, so the younger generation didn’t have too many problems.

It seems extraordinary to me that the US is still dragging its feet on adopting the metric system. But then, when you look at other things like recognizing global warming, it starts to look consistent.

Footnote: Some strange anomalies occurred in Australia. Mechanics had to have 2 sets of spanners when working on some cars, where (say) the body was made in Australia (metric) and the engine came from the US (Imperial system).

How crazy is that?
sara says:
15 Mar 2008 at 7:40 pm [Comment permalink]
nice idea ,, actually i didnot get confused before because i understand from were each case comes ,, any way but its really usefull for other students that they hate math .. lol they are looking for any thing to say math is hard and confsing
Murray says:
21 Mar 2008 at 8:31 am [Comment permalink]
Hi Sara and thanks for your input.

I am in the process of writing a more detailed proposal about an alternative math notation and I hope to publish it soon.
Living St Vincent Anyormi says:
8 Apr 2008 at 3:25 am [Comment permalink]
I am really upgraded each day I have my lessons from intlmaths.PLEASE I need need more tutorials on trigonometry integrals, partial integrals, integration by parts, reduction formula and its application, multiple integration. Please send a step by step solution to some problems in each case.
Thanks
Murray says:
8 Apr 2008 at 4:48 am [Comment permalink]
Hi Living St Vincent. I am adding to the Interactive Mathematics site all the time. I will keep your requests in mind for future revisions.
Shiva says:
19 Nov 2008 at 1:28 pm [Comment permalink]
why not preserve the parenthesis for function application
and use square brackets for grouping?
Murray says:
19 Nov 2008 at 2:10 pm [Comment permalink]
Hi Shiva. Square brackets are suggested as an attempt to be consistent with Mathematica's notation.

Personally, I think either is fine, as long as they are different!
Josh Ribakoff says:
2 Jan 2009 at 5:59 pm [Comment permalink]
It is of note that the square brackets are used to denote array access in modern high level programming languages ( arrays = vectors / matrixes ). This could also lead to some ambiguity but I think the general gist of what you are saying makes sense, and I'm no expert in math.
programaths says:
21 Mar 2009 at 5:41 am [Comment permalink]
I disagree with you notation because it's moving the problem around.

If a student expand "sin(a+b)" in "sin a+sin b" that mean that this student don't understand that sin(a+x) means the function sin() applied to "a+x".

In other words, you could explain that "+","-" etc are in fact binaries function. So you can write "a+b" as "s(a,b)".

Then when you see "sin(a+b)" this is like "sin(g(a,b))" and there is no reason to distribute.

So when you write "5(a+b)=5a+5b" it's like : "p(5,s(a,b))=s(p(5,a),p(5,b))"

If they are able to write it that way, they should avoid the error in the future.
Murray says:
21 Mar 2009 at 7:02 am [Comment permalink]
@Programaths: If they are able to write it the way you suggest, they would not be the ones having trouble with the expression sin(a+b).

Our aim is to make life simpler, not even more confusing.
Reynir says:
12 May 2009 at 7:37 pm [Comment permalink]
I completely agree with the proposed changes to the notation. In my experience, kids most often give up on math before they manage to see past the confusing/inconsistent notation.

I'm definately going to make use of this in the future.
nicks says:
21 Aug 2009 at 5:51 pm [Comment permalink]
When writing by hand, I like to distinguish function abbreviations (such as sin, log, ln, f) from variables by writing them in a script style, as in formal handwriting. Variables are simply printed in simple san-serif style as always. When typed, I've seen that we are supposed to put variables in italics to distinguish them as variables, though I haven't bothered as I don't care for the look.

As for derivative symbols, a neat alternative I found is to use subscript of the variable that the derivative is with respect to. So, for a function f(x) (I'd have made the f in script style if I could), its derivative would be fx(x) (I'd have made the first x subscript on the f here if I could). The chain rule can be written thusly: given y=f(g(x)), the derivative of y with respect to x could be written f[subscript g][multiplication dot]g[subscript x](x). Anyway it's more of an exercise for my own satisfaction to make concisely written notes, as students would be learning the other notations for decades to come I imagine.
Murray says:
21 Aug 2009 at 9:37 pm [Comment permalink]
Thanks for your inputs, Nicks.

I also like subscript notation for derivatives, but as you just found, it is a bother to type it on the Web.

For reference, you can type your

f[subscript g][multiplication dot]g[subscript x](x)

as

f<sub>g</sub>·g<sub>x</sub>(x)

and it will look like the following, as you intended:

f_g·g_x(x)
mechagodzilla says:
26 Oct 2009 at 1:41 pm [Comment permalink]
It seems to me that there's actually nothing wrong with the notation, per se. There's an unspoken assumption that is not stated for the benefit of students until maybe 2nd or 3rd year of college, if you're lucky.

Linear functions can be distributed out of their parentheses. This is why you can write int(x+y) = int(x)+int(y) or laplace(x+y)=laplace(x)+laplace(y). However, it's critical to math literacy to recognize that one of the things you have to know about every function is whether or not it's a linear operation on the argument. The four basic operations are all linear--but when you cross into college nobody informs you of when that stops happening. That's the issue.
Chardaire says:
27 Oct 2009 at 1:47 am [Comment permalink]
I am teaching maths for computer scientist at university level. We use the mapleTA system based on the computer algebra system Maple. One problem is that such a system uses a strict functional notation whilst students are used to an operator notation.

For example Maple interprets
sin (x+1)^5 as raising to power five the result of sin applied to x+1.

However in operator notation sin (x+1)^5 is interpretated as computing the sin of (x+1)^5.

Operator notation is undoubtably the notation of choice for the standart arithmetic operations such as *,+,^ etc
No one (except computer scientist in some cases) would write
+(1,*(2,3)) for 1+2*3.

However, my feeling is that the operator notation should be used only for elementary operations. If you start using unary operation notations like sin x, ln x, after introducing sin and ln as functions and you did not give an explanation that operators are associated with functions that can be expressed by a particular notation (which would go too far at low level maths) then you are potentially confusing students.

And then you can confuse them even more when you consider composition: Does sin^(-1)x means arcsin(x) or 1/sin(x)?

If you only use pure functional notation then
sin^(-1) (x) means arcsin(x), sin (x) ^(-1) means 1/sin(x), and sin (x^(-1)) means sin(1/x).
Murray says:
27 Oct 2009 at 3:22 pm [Comment permalink]
Thanks, Chardaire. I think we should never use "^(-1)" when referring to the function sin(x).

So arcsin(x) (or commonly asin(x)) should be used rather than sin^(-1) (x).

Also, csc(x) (or perhaps cosec(x)) should be the convention and we should avoid any use of "sin (x) ^(-1)".

The Maple interpretation of "sin (x+1)^5" is unfortunate and you're right, that would cause more confusion.
kdg says:
12 Nov 2009 at 4:20 pm [Comment permalink]
Thanks for this great knowdge...i like it very much.
Actually i found these types of problems in my life.
According to me these types of symbles are very important for mathematics....Thanks again...!!!
akky says:
15 Nov 2009 at 9:35 pm [Comment permalink]
very bad suggetion step wise ans of every ques must be given
Murray says:
15 Nov 2009 at 10:15 pm [Comment permalink]
Akky - what is it about the suggested change in notation that you do not like?

I'm not sure what the second part of your response is referring to. A change in notation does not necessarily imply any change to the amount of explanation given in a solution, surely?
stephen says:
12 Dec 2009 at 1:20 am [Comment permalink]
ok here is my deal, why is there so many big words that people cant understand? im 15 and i understand everthing fully. The notation is perfect!
Roy Stone says:
27 Mar 2010 at 9:17 pm [Comment permalink]
Hi, Has anyone got an idea of where I could find articles or even books which are related to this subject, as it is my intention to write a small report on the subject of "the problems cause through mathematical notation, in secondary school education" If you can help please contact me through my e-mail.
Roy
gasstationwithoutpumps says:
1 Aug 2010 at 12:00 am [Comment permalink]
The problem has been addressed in almost every computer language that exists. The general consensus of computer language designers is that the problem isn't with the parentheses, but with the use of juxtaposition for multiplication. Using an explicit multiplication symbol (usually "*") eliminates most of the confusion.
Jason says:
14 Dec 2010 at 10:35 am [Comment permalink]
I think a new mathematics notation should be made. In fact I am proposing it right now. It would be a postfix/reverse polish notation kind of thing.

(x) variable
[1] subscript
{x,y,z} array or set elements

converting infix functions:
f(x) = 2x^2 + abs(16x) + 1
g(x) = thirdroot(x) + log2(x) + sin(cos(x))
h(x) = sigma(i=0,infinity,2i+1)

to postfix functions:
f: (x) 2 power 2 multiply 16 (x) multiply abs add 1 add
g: (x) 1 3 divide root (x) 2 log add (x) cos sin add
h: (i) 2 multiply 1 add 0 infinity sigma

This would be harder to read at first but it would be unambiguous and one could evaluate it (aka a computer could) just looking at it going left to right.
Murray says:
14 Dec 2010 at 12:28 pm [Comment permalink]
Hi Jason. Very interesting proposal, and after a few readings (which certainly were slow at first), I can see what you're getting at.

I'm wondering about such liberal use of passive verbs, though - this is generally a no-no when trying to improve readability. But I can see that once you read past each verb, you are then talking about the next algebraic term.

The human brain can always find ambiguity.

"(x) 2 power 2 multiply" could be

(x^2)*2

or

(x^2*2) = x^4

Couldn't it? The first describes a single algebraic entity, the second indicates a requirement to do a numerical process, resulting in a single entity.
Jason says:
14 Dec 2010 at 12:39 pm [Comment permalink]
Let me explain that one. Of course I haven't developed a thorough system or anything but x is the base (1st parameter), 2 is the exponent (2nd parameter). power is the function being called operating on x and 2. That evaluates and then 2 is pushed on the expression stack. Then multiply is called on that (x^2) and 2. x ^ (2*2) would be something like (x) 2 2 multiply power.
Nicolas says:
2 Mar 2011 at 1:55 pm [Comment permalink]
I am currently writing an economics paper and encountering this exact problem. But in my case, I'm tempted to do just the opposite of what you are suggesting. f(x) for the function and g for g*x. Or maybe g*(x)? Not sure yet.
Murray says:
2 Mar 2011 at 5:01 pm [Comment permalink]
Hi Nicolas. To trigger further thought, why not (g)*(x)?
Derick says:
8 Mar 2011 at 1:32 pm [Comment permalink]
I'm glad to find this article. There's not enough focus on this topic. As a young student, I was good at math. As I discovered more and more confusing math notation, it was a big turn-off for me, even though I was considered good at coping with it (similar story with chemistry). Thankfully, I also got into computer programming at an early age and discovered other notations that have to be unambiguous. When I discovered Lisp-style notation, it was love at first sight. For example (I had the following nicely indented across more lines but the blog won't keep the indentation):

(define (g x) (+ (^ x 1/3) (log 2 x) (sin (cos x))))

(define (h x) (? (i 1 (length x)) (+ 1 (* 2 (element i x)))))

(define z (list (g 7) (h 13)))

This kind of notation is called symbolic expression or S-expression. It is quite convenient to work with in an editor that understands S-expressions and provides navigation, manipulation, auto-parenthesis balancing, and auto-indentation facilities. My example is in prefix notation, which makes the rules for interpretation simpler, but S-expressions don't have to be prefix-style.

Some people complain about all the parenthesis, but I've always liked them. There are alternative syntaxes which retain the same logical properties but reduce the usage of parenthesis, but they're not as clean and simple IMO. I'm not claiming S-expressions are the end-all-be-all, and there are other notations I like.

When I heard that there are old math formulas that were discovered much later to be incorrect (via interpreting with a symbolic calculation computer program), I had to laugh, because even the expert inventors of the formulas had problems with the notation.

I'm looking forward to a renaissance of innovation and improvement of math notation, which I think is especially necessary as the world's use of math becomes more complicated, more depended on, and more people need to understand it.
Murray says:
8 Mar 2011 at 4:45 pm [Comment permalink]
@Derick: Thanks for the input on symbolic expressions. Interesting addition to the discussion!
Luther says:
30 Aug 2011 at 4:57 pm [Comment permalink]
I'm 55 and trying to teach myself calculus, still in the early stages. I have taken algebra 3 times, got good grades but hated function notation each time. The real problem is being missed here. Yes it's ambiguous and looks like multiplication without a multiplication symbol, and yes it requires multitasking or using 2 systems of mental coding, so depending on the person it might stop the mind and make you interpret slowly, instead of reading directly, like if I inserted German words into my sentence and you had to stop and remember what they meant or look them up.

The real problem though is psychological regarding the person faced with a new idea. Learning something new is inherently intimidating for most people and therefore motivation is very important. Math teachers are challenged at every step of the way to make their subject interesting. Notation that is visually confusing to the beginner emotionally upsets him and makes him feel stupid and frustrated, even sleepy. I got my wife through her AA math requirements by teaching her to keep her scratch paper as neat and orderly and uncramped as her answer page. She was failing math for one reason only, she was visually overwhelmed and that made her too tense to think clearly.

When a student sees a lot of unfamiliar gibberish it is just plain scary and that makes it easy to quit. On my part, I have yet to find anything difficult about calculus except the way it is being taught, and that includes notation.

As for new notation that can be typed, many brilliant people must have worked on this in order to create computer programs that do math. Most of the comments above are as scary looking to me, a beginner, as f(x) which gives me a rush of adrenalin that puts me into flight or fight syndrome. Maybe it would be better to invent completely new symbols and draw them up in a font creation program and distribute them for free. I disagree with square brackets, for example, because they're already used for something. You have to use something that's not already got dibs on it or it will be automatically rejected by minds already taught to use it for something else. That means current math symbols should not be changed into something else.

No one has ever explained to me why there should ever be any such thing as function notation, and I haven't been able to guess. Maybe it helps in higher math, but "Calculus Made Easy" by Silvanus Thompson never uses it.

Anyway, this is a fascinating topic and I hope to see something come of it.
Murray says:
31 Aug 2011 at 9:49 pm [Comment permalink]
You've raised some interesting issues, Luther.

We certainly need functions - they are essential for math (and computing, science and engineering), but the notation has certainly got to change!

You're probably right about my square brackets suggestion. I was going for a "different, but not too different" solution, on the grounds if it is way off, no mathematician will ever want to consider it.
Starfall says:
20 Apr 2012 at 2:42 am [Comment permalink]
I do not know why parantheses are used with functions but it makes sense to me.

First of all, the programming languages that currently exist in the world use parantheses both as precedence operators and function parameter indicators, just like we do, so I think it is kind of a curriculum.

If parantheses indicate precedence, then they also indicate that the function is precedent in the operation, which means it should be evaluated first and nothing else should be done before it. I do not think that the confusion of terms like cos(x+y) = cos x + cos y rather than cos(x)cos(y) - sin(x)sin(y) come from this. It is because nobody ever presented a proof why it should be the second case. If no proof is present, students tend to do what you said: They apply the distributive property. And I do not see this any sensible when there are literally hundreds of ways to prove this expression.
Murray says:
20 Apr 2012 at 6:39 am [Comment permalink]
@Starfall - Your answer is very much from a mathematician's (or math teacher's) point of view, not a math user's. That is, 99% of our students will use math, but will never be mathematicians. So whether you prove the expansion of cos(x+y) or not, they will still tend to default to the general meaning of what they see. They will remember what makes sense at the time.
Devon McCormick says:
10 May 2012 at 12:39 am [Comment permalink]
I use a programming language called J which is an executable mathematical notation. The creators of the language have chosen the symbols of the language very carefully and a particular set of them is relevant to this discussion.

The symbol for "power" is "^" and the symbol for "log" is "^." so the related ideas are clearly linked. As are all J symbols, these both have both a monadic (single right argument) and a dyadic (left and right argument) use.

The language is interactive, so if I enter
^1 2 3
(monadic power assumes base "e"), I get
2.71828 7.38906 20.0855
as my result.

Similarly, entering
2 ^. 2 4 6 8
returns the base 2 log of these numbers:
1 2 2.58496 3

The language is free, open-source, and runs on Windows, Linux, and Mac. You can find out more about J at jsoftware.com. Explanations of the use of the power and log symbols is on their site under "help/dictionary/d200.htm" and "d201.htm".
Murray says:
12 May 2012 at 8:13 pm [Comment permalink]
Thanks, Devon. J is new to me and this opens up several interesting possibilities.

Thanks for sharing.
Terry Provost says:
17 May 2012 at 12:07 am [Comment permalink]
I have similar concerns, and appreciate your effort in putting this together. Thanks.
Terry Provost says:
17 May 2012 at 12:30 am [Comment permalink]
Is a totally consistent mathematical notation possible?

Is your answer to the question provable?

The fact that notation is not consistent is prima facie evidence that one is not possible.

Even if one could be found, you would have the problem of "legacy notation": that you would have to preserve the old inconsistent notation in order to be able to interpret older documents that employed it.

Superimposed on top of this (and I think evident in the comments above) is the rendering of these issues in ASCII or Unicode (and which rev of unicode?)

And perhaps a separate issue (I can't believe I'm even saying this) is the font. Some fonts do not visually distinguish between uppercase "i", and l. So Ill may be interpreted as the Roman numeral 3 or a human sickness.

(It seems, as I suspected, font is not determined by unicode.)
Mike says:
10 May 2014 at 1:18 pm [Comment permalink]
Time to revive a moribund post! As you've diplomaticallyl addressed, Murray, many of the suggestions above come from the perspective of individuals already immersed in either programming, mathematics, or both, and conflate "visually identical to" with "conceptually similar to" and make suggestions that disambiguate the notation from a theoretical standpoint. That's not what my students have trouble with. It's simply remembering that the function whose name is "f" is operating on some independent variable(s), which is a different scenario from some variable whose name is "f" being multiplied to some other expression. f(a + 1) in either case, for example.

Here's the most recent I've heard: Why not subscripts? We already do this for sequences (in practice, functions on the whole numbers).

E.g. Define f_t = 1/t, so f_2 = 1/2, f_{a + 1} = 1 / (a + 1) and so on.

This is consistent with mathematicians since subscript either (a) have no consistent meaning or (b) imply the index of a sequence, with which this is still consistent. It's also visually different from parentheses which solves the original "distribution error" without presenting something so radically new that it stops the hearts of burgeoning algebra students.

This does create interesting new conundra like "what to do with log_n?"
Kenneth says:
23 Mar 2015 at 8:38 am [Comment permalink]
Concerning "logarithm".

Let me talk about that from a notational point of view.
By that, I will adress the topic of "logarithm" from a non-historical vantage point and with a sort of naïve sensibility.

Let us start with "multiplication", namely *.
Alright, a ton of stuff has been said about "multiplication" throughout the years, so I will suffice with the following idea:

If one wants to multiply the same number by itself n number of times, one can easily do so by introducing "exponentiation", namely ^.
that is

(1) x^y=z

I
Now, if one were so inclined, one might be interested in solving the equation (1) according to z.
This is - in a sense - a bit banale; it is simply calculating x to the power of y, and lo, one will find z.

II
However, if one were otherwise inclined, one might be interested in solving the equation (1) according to x.
In doing that, there are certain 'syntactical' considerations to be made beside the notational considerations.
When solving x^y = z according to x, we want to isolate x on one side of the equality, and to do so - intuitively - we would want to cancel y, and seeing as y is on the right side of the in-fix, namely ^, it would make sense to cancel y from the right side; and we can remember that when something is cancelled on one side of an equality, it must be introduced on the other side of the equality.
So let me suggest the following notation, namely the in-fix V:
x^y = z
(x^y)Vy = (z)Vy
x = zVy

This, of course, is an alternative way of expressing "the nth root".

III
As to solving the equation (1) according to y, well, we would like to isolate y on one side of the equality. So we need another in-fix.
So let me suggest the following in-fix, namely U:

x^y = z
xU(x^y) = xU(z)
y = xUz

This, of course, is an alternative way of expressing "logarithm"

A)
So, using the "exponentiation" ^ it is rather pro-intuitive.
If you want to cancel something on the right side of ^,
you do it from the right side with V:
x^y = z
(x^y)Vy = (z)Vy,

if you want to cancel something on the left side of ^,
you do it from the left side with U:
x^y = z
xU(x^y) = xU(z).

B)
Using "the nth root" V is pro-intuitive in one case, but counter-intuitive in the other case.
If you want to cancel something on the right side of V,
you do it from the right side with ^:
xVy = z
(xVy)^y = (z)^y
x = z^y,

if you want to cancel something on the left side of V,
you do it from the RIGHT side with U:
xVy = z
(xVy)Ux = (z)Ux
y = zUx

C)
Using "logarithm" U is pro-intuitive in one case, but counter-intuitive in the other case.
If you want to cancel something on the left side of U,
you do it from the left side with ^:
xUy = z
x^(xUy) = x^(z)
y = x^z,

if you want to cancel something on the right side of U,
you do it from the LEFT side with V:
xUy = z
yV(xUy) = yV(z)
x = yVz

Let me summarize the suggested notation(s).

(x^y)Vy = x = (xVy)^y;
yU(y^x) = x = y^(yUx);
yV(xUy) = x = (yVx)Uy

Now, of course, one has to take into consideration, what values are being used;
and/but one ALWAYS has to take into consideration, what values are being used - no matter which notation is used.
Murray says:
24 Mar 2015 at 4:23 pm [Comment permalink]
@Kenneth: Thank you for the interesting suggestions. The inverse relations become quite clear.

Of course, U and V could look a lot like ∪ (union) and ∨ (logical or), so that may lead to some confusion.
Devon McCormick says:
2 May 2015 at 4:13 am [Comment permalink]
Regarding Kenneth's comment - the J language does all this. For example, here's a J session (my input is indented three spaces, J's output is flush against the left margin):
```
   10 ^ 3
1000
   10 ^. 10 ^ 3
3
   3 %: 10 ^ 3   NB. "3 %:" is the 3-root (cube-root)
10
```
One simplification J makes is that it does away with built-in "operator precedence" - everything is evaluated right-to-left.
Murray says:
2 May 2015 at 8:26 am [Comment permalink]
@Devon: Thanks for the insight into J language. It's new to me and could be very useful.
Kenneth says:
22 Sep 2015 at 9:38 am [Comment permalink]
@Murray: You are correct(!) The symbols, that I have chosen, only create more confusion...

Now, my consideration was not so much a notational one, as it was a syntactical one.
I am mainly considering the syntax of the symbols;
However you have made me also consider the symbols themselves.

When using addition, namely $+$ :
${x}{\stackrel{{{\mathbf{U}}}}{+}}{y}=\frac{1}{x}\times{y}$

${x}{\stackrel{{{\mathbf{\Lambda}}}}{+}}{y}={x}\times{y}$

${x}{\stackrel{{{\mathbf{V}}}}{+}}{y}={x}\//{y}={x}\times\frac{1}{y}$
This might not be completely necessary...

When using multiplication, namely $\times$ :
${x}{\stackrel{{{\mathbf{U}}}}{\times}}{y}={\log}_{x}{\left({y}\right)}$

${x}{\stackrel{{{\mathbf{\Lambda}}}}{\times}}{y}={x}^{y}$

${x}{\stackrel{{{\mathbf{V}}}}{\times}}{y}={\sqrt[{y}]{x}}={x}^{{\frac{1}{y}}}$
This might be useful(?)
Murray says:
22 Sep 2015 at 10:47 am [Comment permalink]
@Kenneth - Your latest suggestions make more sense to me.

They are a somewhat nightmarish to type, and this would reduce the likelihood of adoption, unfortunately.

BTW - good on you for using the math-in-comments option!
Kenneth says:
22 Sep 2015 at 10:49 am [Comment permalink]
Furthermore...

Let
q ${x}$ p ${\stackrel{{\text{def}}}{=}}{\log}_{2}{\left({x}\right)}$
and
d ${x}$ b ${\stackrel{{\text{def}}}{=}}{2}^{x}$

Let us consider FIELD-theory.
We shall use the term ADDITION and the term MULTIPLICATION:
an ADDITION need not be (usual) addition; and
a MULTIPLICATION need not be (usual) multiplication!

1)
For instans, we can say,
that ${\left({\mathbb{R}},+,\times\right)}$ is a field with addition and multiplication, for
${\mathbb{R}}={\left(-\infty,\infty\right)}$ and
${x}+{y}{\stackrel{{\text{def}}}{=}}{x}+{y}$ and
${x}\times{y}{\stackrel{{\text{def}}}{=}}{x}\times{y}$

2)
however, we can also say,
that ${\left({S},\times,\star\right)}$ is a FIELD with ADDITION and MULTIPLICATION, for
${S}={\left({0},\infty\right)}$ and
${x}\times{y}{\stackrel{{\text{def}}}{=}}$ dq ${x}$ p+q ${y}$ pb and
${x}\star{y}{\stackrel{{\text{def}}}{=}}$ dq ${x}$ p $\times$ q ${y}$ pb

3)
MULTIPLICATION need not be the iteration of ADDITION
such that $\exists{x},{y}\in{S}:{x}{\stackrel{{{\mathbf{\Lambda}}}}{\times}}{y}\ne{x}\star{y}$
Jon says:
1 Jun 2016 at 7:51 am [Comment permalink]
A very basic starting suggestion:
When multiplying A by B

Always write out
A*B

NOT
AB
A(B)

This way the parentheses () will always be used for order of operations.
I think someone mentioned this too, but I like the idea so I'll repeat:
Use [] and {} for other things, like functions and coordinate points.

As far as trigonometry:
Start fresh.
Why use the Latin derived "sine, cosine, tangent" to define the functions?

Give each side and angle of the right triangle formed by the reference angle a letter.

So if

referenceAngle = ∠CAB
complementAngle = ∠ABC
rightAngle = ∠BCA

OppositeSide = SideA,
AdjacentSide = SideB
Hypotenuse = SideC

Sin= O/H = B/C
Cos= A/H = A/C
Tan= O/A = B/A

Then to get inverses, just use
1/(B/C) = C/B
1/(A/C) = C/A
1/(B/A) = A/B

It's a bit hard to put this in words; unfortunately, I don't know any coding, so I can't show a proper picture.
I hope I'm making sense, and I'll be happy if anyone replied!
Murray says:
1 Jun 2016 at 11:20 am [Comment permalink]
@Jon: I basically agree with both your suggestions.

As for the trigonometry ratios, why not just use O/H, A/H and O/A? (But then again, O looks too much like 0, so maybe not such a good idea...)
Chrona says:
23 Feb 2017 at 12:59 am [Comment permalink]
hiya so your math notations are quite nice indeed however im not sure of how you'd get these answers. of what "sin" or "log" is to mean and it's frankly very confusing, I'm not even sure of what the "f" stands for.. I'm doing this home schooling shtick and I was looking for some helpful articles and this one is very, however things just don't add up.. I hope I'm making sense, and I'll be happy if anyone replied!

Towards more meaningful math notation

66 Comments on “Towards more meaningful math notation”

Leave a comment

Comment Preview

Tips

Categories

Most Commented

Recent Trackbacks

SquareCirclez is a "Top 100" Math Blog

Towards more meaningful math notation

Related posts:

66 Comments on “Towards more meaningful math notation”

Leave a comment

Comment Preview

Tips

Categories

Most Commented

Recent Trackbacks

SquareCirclez is a "Top 100" Math Blog

Want Better Math Grades?

Want Better Math Grades?

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.