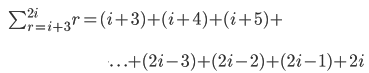Summation notation part 2
By Murray Bourne, 20 Feb 2006
Explanation
This is Part 2 of a (lengthy) exchange between a reader and myself regarding a particularly troubling summation notation question recently.
See the beginning of it here:
Continuing...
Hi again sir
Thanks for replying back sir
Crazily, would it be ...
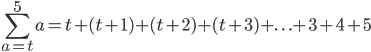
???
and the same for ...
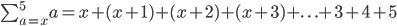
???
Thanks for your help sir and I can't stop saying sorry because I know it must frustrating - I didn't know that for even a variable value, the same would apply when writing down the last few terms as natural numbers (specifically in this case).
Thanks again sir and sorry once again 🙁
Yousuf.
OK, Yay!! It is now correct!! Your first terms and last terms are now 100% perfect.
Now, please read the whole page again - especially the bits where I tried to convince you there is not 5 terms just because there is a 5 at the top, There can be hundreds of terms!
Then, when you are sure you have a handle on the expansion, write out the first few terms, the "..." and the last few terms for:
(This one never got answered properly before)
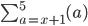
This one is new:
Hi again sir
Right, so drawing on everything done so far.
When using sigma series, the quantity at the top denotes the terminating term and the quantity at the bottom of sigma denotes the initiating term.
So for
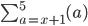
This would be ...
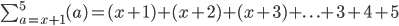
The starting term is x + 1 and the terminating quantity is 5. They follow the pattern of natural numbers in that we +1 to the previous term after a.
Also,
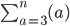
Would give ...
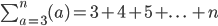
This is because the starting term is 3 and the terminating quantity is n (which in essence goes on forever). They follow the pattern of natural numbers from 3 onwards by adding +1 to the previous term after a.
Is that OK sir?
Thanks again for your help sir! 🙂
Yousuf.
First one is excellent.
Second one - no, it doesn't go on forever. It goes up to the value of some "n" which we can define, or find if we have more information. It will only go on forever if the top number is infinity (in which case we would have "+ ..." at the end of our expansion. You correctly do not have that at the end).
When writing them out, please include the first few terms (like you did in both of them above, then the "...", then the last few terms before the final number (like you did in the first one but not the second one.
(1) Do the second one again and include the last few numbers before n. (Why? So I am convinced you know what is happening.)
(2) New one (also include the first few terms and the "..." and the last few terms before "2n"):
Hi again sir
Sorry about the wording of the second one sir but please correct me if I'm wrong on the reowrding because I actually meant that the pattern continues until it reaches the required quantity n unless I'm wrong sir.
So it'd be ...
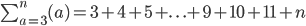
The second one I think should be ...
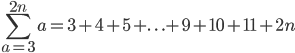
???
But sir, apparantly, the textbook shows that we should ideally write the above as. ..
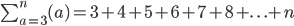
and
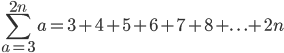
But I can see why we're using the "+...+" before the last few terms to gesticulate that the pattern proceeds in the pattern shown in the first few terms, but I'm just commenting on what the book defines in its way sir.
Thanks again sir, I really appreciate your help 🙂
Yousuf.
Where does 9, 10 and 11 come from?? What is 1 less than n (this will be the second last term)? What is 2 less than n (this will be the 3rd last term)??
The first one should be:
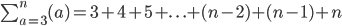
You only actually need 3 terms to indicate what is going on, not 6 as your textbook says. It doesn't hurt to have 6, you just don't need any more once the pattern is clear. And you have to show the last 3 terms, as I keep saying.
Try this again:
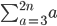
And here's another new one:
Show the first 3 or 4 terms, the "..." and the last 3 or 4 terms. There is no 9, 10 or 11 involved.
Hi again sir
Sorry sir, I have to apologise here: the ...+(n-2)+(n-1)+n part is new to me at the moment because thus far, the textbook has required only to show the first three/4 terms, then use the +...+ notation and then end it with a general rule. So like the textbook writes the following example as...
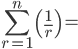
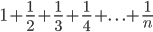
That's what I've been writing down thus far and I wasn't aware that the way you corrected me on the first one of those examples was actually the better way to write it and it's just my personal opinion to say that I believe the textbook should echo how you've written it because surely at A-level, the textbook should be showing this clearly, but they've just helped students take one small step from GCSE and in all honestly, the textbook doesn't even show anything like the way you wrote this one
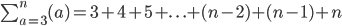 a
a
nd from now on I would prefer to take this route.
I wrote this
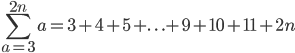
because I thought we use +...+ to convey the pattern, and then terminate using the last 3 terms: the 2 from the last terms to gesticulate the pattern and end it with the general rule. I can now see why it's important to corroborate the lead-up of the general rule.
But, as you say sir, would the proper written manner be, for the fraction one ...
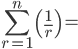
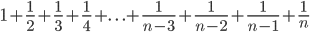 ???
???
So in essence, we're just reversing as we approach the general rule (where we +1 all the time using natural numbers and when approaching the general rule, we go backwards until we reach the general rule - not quite sure how I can reword that sir!!)
Anyway, would this one be ...
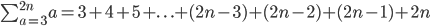 ???
???
Adn then
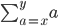
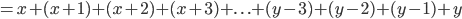 ??
??
Thanks sir 🙂
Yousuf.
Yay - all the ones you just did are good - the fraction one, the "2n" one (9, 10 and 11 will only be involved in those positions if n=6, and we don't know that to be true) and the "y" one.
So now, try this one:
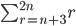
Hi again sir
Sorry for the late reply sir.
This one looks a little unsettling sir, particularly the ending, so I'll plan my way through. We substitute r = n+3 into r and then add +1 to each consecutive term.
TERM 1 TERM2 TERM 3 TERM 4
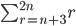
![= [(n+3)]+[(n+3)+1]+[(n+3)+2]+[(n+3)+3]+ . \ . \ .](/blog/wp-content/images/2010/06/images/EXTERN_0062.png)
Right, the last part is a little confusing, so this is what I've done. I've stated that the terminating term is 2n and we subtract our way using reversed natural numbers until we reach 2n isolated.
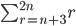
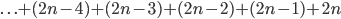
I couldn't correctly figure out if n + 3 would be involved in the foregoing, so I get ...
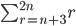
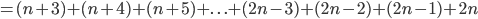 ???
???
Thanks again sir,
Yousuf
Perfect! (I've noticed the more question marks you have at the end of your answer, the more correct it is ^_^)
Now, I'm not sure whether you recognised that last summation question, but in fact, it is part of the question you originally started with (right at the top of this page).
I hope you have a better idea what that question is asking now.
Do you think you can answer it?
Hi again sir
Actually, I didn't take notice of it! I'll try and see if I can solve it sir.
The question is
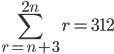
which is saying that the starting term of the sequence of natural numbers (r) is n + 3 and the terminating term is 2n.
I think it's saying that the sum of the series of natural numbers, where the first term is n + 3 and the terminating term is 2n, is 312.
So... if I can draw back from the previous work, I did ...
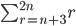
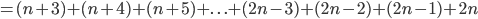
And also
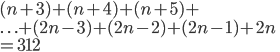
I'm still not sure what the notation is to solve this equation. DO I do this sir: do I take the first three terms and the last four terms thus ...
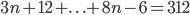
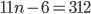
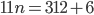
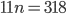
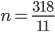 !!!!!!!!!!!!!! That can't be right!!!
!!!!!!!!!!!!!! That can't be right!!!
But lets see if we can use AP notation involving 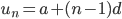
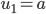
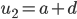
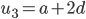
We know that from the series
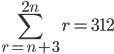 , the first term is r = n + 3, so this gives ...
, the first term is r = n + 3, so this gives ...
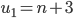 using
using 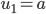
Also,
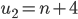
But the last term is a variable so
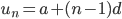
so
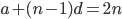
Sorry sir if it's confusing, but that's as far as I can go.
Sorry sir and thanks again, 🙂
Yousuf
(1) There are 2 formulas for the sum of an AP. What are they?
(2) For both formulas, you need to know the number of terms in your AP. So how many are there?
BTW, it's a shame they've used "n" in the sum sign - it will be confusing later. Let's make a slight change now, and then explain why later.
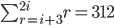
So here is your expansion using "i" instead of "n".
Trust me - it will be easier using "i" from now on. We will find the value of "i" then just change it back to "n" at the end.
Hi again sir
Oh yea! I was thinking about the sum formulas!!
(1) The formula for the sum of an AP is given by...
![S_n=\frac{n}{2}[2a+(n-1)d]](/blog/wp-content/images/2010/06/images/EXTERN_0080.png) and also
and also 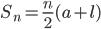
(2) "Find the number of terms in the given sequence"
We know that ...
a = (i + 3)
u_n = 2i
d = 1 (common difference is +1)
We can use 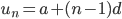 ...
...
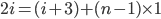
I can see why there is the confusion (n = 2n)
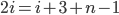
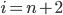
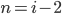
Is that right sir? There are (i - 2) number of terms ?? (+ !!) That can't be right can it?
Thank you sir 🙂
Yousuf
Yes, correct. The number of terms is i-2.
You are extremely close, now to the final answer!!
Use the second sum formula (it's less messy).
(a) You know the number of terms - plug it in (i-2)
(b) You know the first term - plug it in (i+3)
(c) You know the final term - plug it in (2i)
Now go back and read the original question again (top of this page) and figure out what you need to do with the 312.
You should end up with a value of i at the end.
^_^
Thank you so much for replying back sir 🙂
Righto, we use
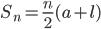
We know that
-
n = i - 2
-
a = i + 3
-
l = 2i
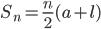
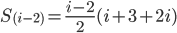
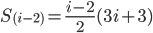
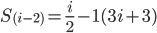
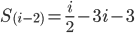
Making the denominators common with for i:
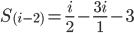
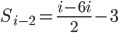
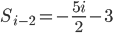
Is that right sir?
Because I'm suggesting now that we should solve for i (which is n) ...
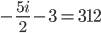
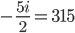
Changing the notation to a more easier format ...
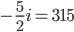
Multiplying by - 2/5 ...
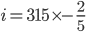
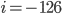
So in essence, 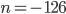 ??
??
That's not right is it sir??
Yousuf.
Up to this line you were correct:
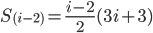
Next should be:
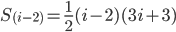
Keep going...
So we expand the brackets first to get ...
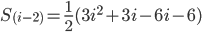
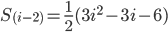
Then ...
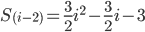
We know that
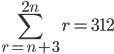
So ...
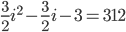
Multiply by 2 throughout ...
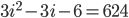
So ...
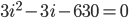
Then ...
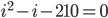
We need to solve this quadratic (sir, is it true we are using only the positive solution to this because the negative solution will be senseless?) ... two factors of 210 are 14 and 15 and we get -1 (coefficient of i) by doing 14-15 and since both numbers are + and -, we know that positive x negative = negative (as required for -210), so ... (actually I cheated here using GeoGebra!, but we should be able to do this using graphics calculators in the tests) ...
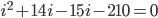
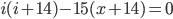
Therefore,
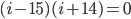
We change i back to n and get ...
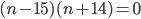
So, the roots are 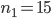 and
and 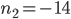
Because we need the positive solution, the solution to the problem is n = 15.
We did it - yay!!! 😀 Many thanks to you sir for helping me in this sir !!
Thank you very much 🙂
Yousuf.
You're welcome, Yousuf!
Of course, you should substitute your answer into the original summation expression to ensure you are correct. this also helps you to understand what you have done.
And that's the end!
Be the first to comment below.