IntMath Newsletter: squaring circle, 17 equations
By Murray Bourne, 27 Dec 2016
27 Dec 2016
In this Newsletter:
0. PhotoMath - what I should have said
1. Squaring the circle with rope
2. East Asian countries perform best in TIMMS
3. Resource: 17 equations
4. 2016 in review
5. Math movies: Unexpected math
6. Math puzzles
7. Final thought: tolerance
0. PhotoMath - what I should have said...
In the last Newsletter I mentioned the product PhotoMath. Reader Forrest correctly pointed out in the comments that:
PhotoMath is a great app for students to cheat on math tests with their cell phone. You should not be publicizing this app.
I agree that such tools (including even the humble calculator) can be used to "cheat", so I added the following disclaimer:
"PhotoMath, like all such computer-based math solving tools, should ONLY be used to check your own work (which helps you to learn) - NOT to simply solve the homework for you (which usually results in your never knowing it)."
1. Squaring the circle with rope
I've had an interest in the problem of "squaring the circle" (finding a square with the same area as a given circle, using straight edge and compass only) for some time now. I named this blog "SquareCirclez" in memory of the challenge.
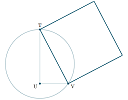 |
I recently came across a solution by Jonathan Crabtree using rope. This could be turned into an interesting class exercise. I developed an animation of the method including a proof. See: Squaring the Circle: rope method |
2. East Asian countries perform best in TIMMS
One of the reasons I moved to Singapore 20 years ago was because of its strong showing in international comparisons of math and science achievement. I wanted to know how they did it.
Singapore, as well as other East Asian countries, once again performed well in the 2015 results, published recently. From the report:
Singapore, Hong Kong SAR, Korea, Chinese Taipei, and Japan continue outperforming all participating countries in mathematics at the fourth and eighth grades, maintaining a 20 year edge according to results released today from TIMSS, the longest running, large scale international assessment of mathematics and science education in the world.
Pisa, too: From Singapore's Straits Times, How Singapore's students rose to No. 1, we read:
Earlier this month, 15-year-olds in Singapore were ranked No. 1 in maths, science and reading in the 2015 Programme for International Student Assessment (Pisa) test, dubbed the "World Cup for education".
The New York Times chimes in with What America Can Learn From Smart Schools in Other Countries.
You may be interested in these related IntMath articles:
- Why East Asians do well in math
- Math tests and rice paddies
- Singapore math - some research on its strengths
- Japanese-based math textbooks the answer?
3. Resource: 17 equations that changed the course of history
Ian Stewart's book In Pursuit of the Unknown: 17 Equations That Changed The World is an outline of how some very significant equations have driven many of the technologies and improvements to our lives. Some of the 17 equations you already know (like Pythagoras' Theorem and E = mc2), and you'll come across many of them in your undergraduate studies if you intend to become a scientist or engineer. It's always good to read over the equations in advance to get an idea what the variables and notation is all about, before you study the topics.
 |
Here's the list of equations with a brief explanation of each by Andy Kiersz of Business Insider. How many of them do you know? |
4. 2016 in Review
Here are the most popular IntMath articles (based on traffic) during the year - some are new, and some are evergreens.
Number theory
The Twelve Days of Christmas - How Many Presents?
Functions and Graphs
Conic Sections - interactive 3-D graph
Inverse trigonometric function graph animations
Applications of Radian Measure
Polar to Rectangular Online Calculator
Domain and Range of a Function
How to find the equation of a quadratic function from its graph
How do you find exact values for the sine of all angles?
Calculus
Derivatives of the Sine, Cosine and Tangent Functions
Fourier Series Graph Interactive
5. Math movies: Math in unexpected places
 |
Here's a collection of 8 TED talks that talk about aspects of mathematics which may surprise you. |
6. Math puzzles
The puzzle in the last IntMath Newsletter asked about a number in "decimal form".
Correct solutions with explanation were submitted by Chris, Saikrishna, Γιώργος, Francis, Bill, GuidoV, Eamon, Hamid, Nick, Bruce, Thomas, Gerard, and Peggy. (Whenever answering a math question, it's always best to explain where your answer came from!)
New math puzzle: 2017
Use the digits in the year 2017 and only the operations +, −, ×, ÷, sqrt (√, that is, square root), ^ (raise to a power), ! (factorial), and !! (double factorial) along with grouping symbols, to write expressions for the counting numbers 1 through 100. Try to use the digits in the order 2, 0, 1, 7 as much as possible.
You can leave your responses here.
7. Final thought: tolerance
My hopes for 2017 are that we'll have a more tolerant world, but wise leadership in this area is becoming rarer. The first deaf and blind person to earn a Bachelor of Arts degree once said:
The highest result of education is tolerance. [Helen Keller]
Happy New Year everyone and I wish you a healthy - and tolerant - 2017.
Until next time, enjoy whatever you learn.
See the 8 Comments below.
27 Dec 2016 at 7:53 pm [Comment permalink]
Enjoyed the clarity of your proof on squaring the circle.
----------
We live near a Japanese Sorobon school.
After several years the student can mentally see the device
and perform world class mental math.
While arguably a waste of time, it shows how western
education misses the minds eye.
As a teacher find a "draw it to know it" approach is effective.
(believe Einstein said he could see his physics, but had to hire
math guys skilled in tensors).
----------------
Perhaps that is why your online proofs are so appreciated.
ct
27 Dec 2016 at 8:45 pm [Comment permalink]
Interesting point! My wife learned soroban as a child. To this day, she uses an imaginary soroban with her fingers (good muscle memory) when doing mental arithmetic tasks.
28 Dec 2016 at 11:18 am [Comment permalink]
Short note on "squaring the circle"
I looked for an "algebra" solution.
The desired square centered at the circle center has (1)it's four corners "outside" the circle and (2)four arc sectors are "outside" the square.
Let x be 1/2 the length of a side of the desired square,and
As = area of arc segements
Aq = area of four corners outside the circle.
r = radius of circle
As must equal Aq.
(2x)^2 = pi(r^2)- As
(2x)^2- (pi(r^2)- As) =Aq
(2x)^2 -(pi(r^2)= Aq - As =0
Then, 2x = sqr(pi)(r)
Area of square (sides = 2x) = (2x)^2 which is pi(r^2)
QED
29 Dec 2016 at 3:24 pm [Comment permalink]
Thanks, Don!
24 Jan 2017 at 6:12 pm [Comment permalink]
Tolerance is wonderful but maybe not depending on the context.
What is more intolerant than maths? - I remember being a student and later teacher where examinations, mine or others, were of great importance. I often reflected that in, say, an English exam, a student might waffle convincingly or at least start waffling prior to getting an answer in order. In Maths, if you didn't know or had forgotten, there was no way of bluffing - That's intolerance for you! Back to the wall, 2 + 2 = 4 , tolerate anything else at your peril
24 Jan 2017 at 6:18 pm [Comment permalink]
@Paul: Sadly, for many students that describes their experience well. They rarely have a chance to discover or brainstorm, since the main aim is to get the (one) correct answer. Intolerant, indeed...
28 Jan 2017 at 8:59 pm [Comment permalink]
2017
I forgot about this problem over the holiday period.
This is my interpretation of the problem.
In each case I have used the digits 2, 0, 1, 7 each time and sometimes more than once for each number.
On the right hand side after the colon (:) there is brief explanation.
For example [9] means the expression for the number 9.
Here goes.
1 = -{(2 + 0 + 1)! - 7} OR 2 + 0 -1 + 7 x 2 x 0 x 1 x 7
2 = 2 + 0 x 1 x 7
3 = sqrt(2 + 0 x 1 + 7) OR 2+ 0 + 1 + 7 x 2 x 0 x 1 x 7
4 = -(2 + 0 + 1 - 7)
5 = -(2 + 0 x 1 - 7)
6 = 2 x 0 -(1 - 7)
7 = 2 x 0 x 1 + 7
8 = {-(2 + 0 + 1 - 7)}!!
9 = 2 + 0 x 1 + 7
10 = 2 + 0 + 1 + 7
11 = 2 + 0 x 1 + 7 + 2 + 0x1x7 : [9] + [2]
12 = -(2 + 0 x 1 - 7) + 2 x 0 x 1 + 7 : [5] + [7]
13 = (2 + 0 + 1)! + 7
14 = (2 x 0 x 1 + 7) x (2 + 0x1x7) : (7) x (2)
15 = {- (2 + 0 x 1 - 7)}!! OR (2 + 0 + 1)! + 7 + 2 + 0 x 1 x7
16 = { - (2 + 0 + 1 - 7)}^(2 + 0 x 1 x 7) : [4] squared.
17 = {-(2 + 0 x 1 - 7)}!! + (2 + 0 x 1 x 7) : [5]!! + [2]
18 = (2 + 0 + 1) x 7 - sqrt(2 + 0 x 1 + 7)
19 = 2 + 0 x 1 + 7 + 2 + 0 + 1 + 7 : [9] + [10]
20 = (2 + 0 + 1 + 7) x (2 + 0 x 1 x 7) : [10] x [2]
21 = (2 + 0 + 1) x 7
22 = {- 2 + 0 + 1 - 7)}! - 2 + 0 x 1 x 7
23 = (2 + 0 + 1) x 7
24 = {-(2 + 0 + 1 - 7)}! : [4]!
25 = {-(2 + 0 x 1 - 7)} ^ (2 + 0 x 1 x 7) : [5] squared
26 = ((2 + 0 + 1)! + 7) x 2 + 0 x 1 x 7 : [13] x 2
27 = (sqrt(2 + 0 x 1 + 7)) ^ sqrt(2 + 0 x 1 + 7)
28 = -(2 + 0 + 1 - 7) x (2 x 0 x 1 + 7) : [4] x [7]
29 = {-(2 + 0 + 1 - 7)}! - (2 + 0 x 1 - 7) : [4]! + [5]
30 = -(2 + 0 x 1 - 7) x {2 x 0 -(1 - 7)} : [5] x [6]
31 = {-(2 + 0 + 1 - 7)}! + (2 x 0 x 1 + 7) : [24] + [7]
32 = (2 + 0 x 1 x 7)^{-(2 + 0 x 1 - 7)} : 25
33 = {-(2 + 0 + 1 - 7)}! + (2 + 0 x 1 + 7) : [24] + [9]
34 = {-(2 + 0 + 1 - 7)}! + (2 + 0 + 1 + 7) : [34] + [10]
35 = (2 x 0 x 1 +7)!! ÷ sqrt(2 + 0 x 1 + 7) : 105 ÷ [3]
36 = {2 x 0 -(1 - 7)} ^ (2 + 0 x 1 x 7) : [6] squared
37 = (2 + 0 + 1)! x 7 + (2 + 0 x 1 - 7)
38 = (2 + 0 + 1)! x 7 + 2 + 0 + 1 - 7
39 = {(2 + 0 + 1)! + 7} x sqrt(2 + 0 x 1 + 7) : [13] x [3]
40 = (2 + 0 + 1 + 7) x {-(2 + 0 + 1 - 7)} : [10] x [4]
41 = (2 + 0 + 1)! x 7 + {(2 + 0 + 1)! - 7}
42 = (2 + 0 + 1)! x 7
43 = (2 + 0 + 1)! x 7 - {(2 + 0 + 1)! - 7}
44 = (2 + 0 + 1)! x 7 + 2 + 0 x 1 x 7
45 = {-(2 + 0 x 1 - 7)} x {2 + 0 x 1 + 7} : [5] x [9]
46 = (2 + 0 + 1)! x 7 - (2 + 0 + 1 - 7) : [42] + [4]
47 = (2 + 0 + 1)! x 7 - (2 + 0 x 1 - 7) : [42] + [5]
48 = {2 x 0 - (1 -7)}!!
49 = {2 x 0 x 1 + 7} x {2 x 0 x 1 + 7} : [7] by [7]
50 = -(2 + 0 x 1 - 7) x (2 + 0 + 1 + 7) : [5] by [7]
This where I get lazy and cover the last the numbers 51 to 100.
From here on use expressions for 50 and the number Z, where 1 ≤ Z ≤ 50
50 + Z = [50] + [Z]
e.g.
60 = -(2 + 0 x 1 - 7) x (2 + 0 + 1 + 7) + (2 + 0 + 1 + 7) : [50] + [10]
A few alternatives, just to use double factorial and division:
60 = {-(2 + 0 x 1 - 7)}! ÷ (2 + 0 x 1 x 7) : 5! ÷ 2
63 = (2 + 0 x 1 + 7)!! ÷ {-(2 + 0 x 1 - 7)!! : [9]!! ÷ [5]!!
64 = {(-2 + 0 - 1 + 7)!!}!! OR (2 + 0 x 1 x 7) ^ {2 x 0 -(1 - 7)}
75 = {(- 2 + 0 x 1 + 7)!!} x (-2 + 0 x 1 + 7)
30 Jan 2017 at 11:36 am [Comment permalink]
Good on you, Gerard for having a go at the 2017 puzzle!