IntMath Newsletter: Shells, resource, Bitcoin
By Murray Bourne, 12 Dec 2017
12 Dec 2017
In this Newsletter:
0. Season's greetings
1. New on IntMath: Shell method
2. Resource: Mathpix
3. Math in the news and Math movie: Bitcoin
4. Math puzzle: Triangles
5. Final thought: No more cars?
0. Season's greetings
'Tis the season for Hanukkah (starts today), Christmas (25th Dec or 7th January), New Year (1st January and many other dates in other countries) and other celebrations. Whatever you celebrate, I hope next year is full of health, peace and good learning.
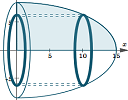
1. New on IntMath: Shell method
There have been a lot of reader requests for a page on Shell Method. Some of the 3D mental gymnastics you need to do for this topic can be quite challenging, but there are some great applications using this method of finding volumes using integration.
 |
See: |
2. Resource: Mathpix
Mathpix is a clever math solver that can read hand-written math using your mobile's camera.
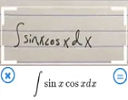 |
It makes use of a math solver, Desmos and some other tools to solve problems and graph results. See: Mathpix (available in Android and iOS versions) |
It's quite well done and has a lot of promise, but I found the results somewhat "clunky" at times. (It quite often misread math, even printed examples.)
This provides us with yet another dilemma, similar to the one discussed when I mentioned Photomath last year. Such tools can help students learn math, but there is always the fear students will just use the tool to do their homework for them and just copy-paste, and will learn very little.
What such tools really should inspire is a completely different way of going about math education. Rather than it being all about "learning how to do the algebra", it should be about "learning how to use the many available tools to solve real problems."
Disclaimer 1: IntMath has no connection with Mathpix.
Disclaimer 2: Like all technologies, Mathpix can be used for good, and not-so-good.
3. Math in the news and Math Movie: Bitcoin
As I write, the value of bitcoins has surged. To give an idea of how much, here's a quote from Bloomberg:
In 2010, programmer Laszlo Hanyecz exchanged 10,000 bitcoins for two Papa John's pizzas. With the chain's current limited-time offer of any large or pan pizza for $10, that many bitcoins would now buy more than 16 million large Papa John's pizzas.
 |
So what's the mathematics behind bitcoin? This video is from the brilliant 3Blue1Brown: Ever wonder how Bitcoin (and other cryptocurrencies) actually work? |
4. Math puzzles
The puzzle in the last IntMath Newsletter asked about intersecting quadratic functions.
Correct answers with explanation were provided by Tomas, Chris, and C Trenor, who rightly said we should make use of all the tools available. (He suggests Desmos, Symbolab, Wolfram|Alpha and GeoGebra.) In fact, each respondent used a graphics tool to see what was going on, which makes a lot of sense to me.
Also, see: Conic Sections 3D Interactive, where you can investigate in 3 dimensions what's happening when a plane intersects a cone, producing parabolas, hyperbolas and so on. (Move the top slider to 90°, and you'll see one of the "degenerate forms" appear).
You only really understand a math problem if you can do it algebraically, numerically and graphically. Let's look at it all 3 ways.
Numerically
We can easily substitute each of the 5 coordinate pairs into the given equations, and will see each one "works" (that is, the left side of the equation equals the right in each case). However, that doesn't answer the "how is it possible?" part of the question.
Algebraically
Our aim is to solve the following 2 equations simultaneously.
2x2 − xy − y2 − 4x + 4y = 0 ... (1)
6x2 + xy − y2 − 16x + 2y + 8 = 0 ... (2)
We can factor the left side of each of the above. This first involves some observation (there appears to be a common term, (x − y) throughout the first one). We use polynomial division to give:
(x − y)(2x + y − 4) = 0 ... (3)
The second one doesn't have the common term (x − y), so we try the second term from the first factorization, (2x + y − 4) and obtain:
(3x − y − 2)(2x + y − 4) = 0 ... (4)
Since there is a common term between (3) and (4), we only need to solve:
x − y = 3x − y − 2
With some further thought, we can conclude solutions lie along the lines:
y = −2x + 4
OR at the intersection of
y = x
y = 3x − 2
That is, at x = y = 1.
These are just the expressions we found by factoring.
Graphically
This is what Desmos gives us for equation (1). It's actually two intersecting lines, which in this case are degenerate hyperbolas (which occur when a plane intersects a double cone through the tip of the cones):
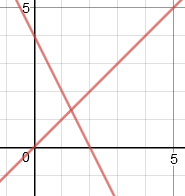
And here's what we get for (2), another set of straight lines:
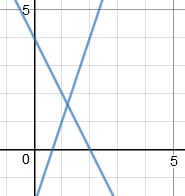
(The above lines are the ones we found algebraically, earlier.)
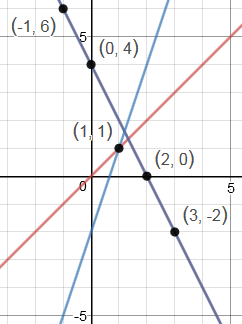
Here's the graph of both degenerate parabolas on the one set of axes. The line through (0, 4) and (2, 0) is y = −2x + 4, the common term in our algebraic solution given above (and is quite dark because the 2 graphs are coinciding).
The graph also shows the 5 intersection points mentioned in the puzzle question:
Other examples
The curves produced by the quadratic function,
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
can be either of the following, depending on the value of B2 − 4AC:
If B2 − 4AC < 0, we get an ellipse, circle, a point or nothing;
If B2 − 4AC = 0, we get a parabola, two parallel lines, 1 line or nothing;
If B2 − 4AC > 0, we get a hyperbola, or two intersecting lines.
Other systems of quadratic equations could produce more than 4 intersection points, for example:
1. Parallel lines (a "degenerate" parabola) and a pair of intersecting lines (a "degenerate" hyperbola), where one of the lines coincides (like we had in the puzzle).
2. Single line (a "degenerate" parabola) and a pair of intersecting lines (a "degenerate" hyperbola), where the single line coincides with one of the intersecting lines.
New math puzzle: Shaded area
It's not exactly the star on top of a Christmas Tree, but this problem reminded me of it.
The first two triangles are combined as shown in the third image.
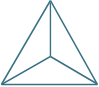
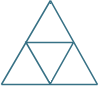
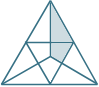
What fraction of the large triangle is the shaded area?
You can leave your responses here.
6. Final thought: No more car growth in Singapore
Singapore is a small island state and it's been my home for over 20 years. I've never owned a car here (they are prohibitively expensive, and I've never wanted one since the public transport is mostly excellent).

Singapore has one of the highest rates of luxury
car ownership in the world [Image credit: Inquirer]
Singapore's 2013 Transport Master Plan (PDF) says
Roads already take up 12 per cent of Singapore’s total land area, compared to 14 per cent for housing.
Most cities worldwide are being choked to death by cars and it's crazy that cars could take up almost the same land area as people.
Singapore announced in October this year that it was cutting the growth rate of all private passenger vehicles to zero. It coincides with a big increase in spending on public transport infrastructure.
Are cars choking your city? Perhaps we need a different approach, and Singapore's policies on this issue mostly make sense to me.
See you again in 2018.
Until next time, enjoy whatever you learn.
See the 20 Comments below.
12 Dec 2017 at 10:53 pm [Comment permalink]
The shaded area S is difference between the area A1 of one small triangle in the first large triangle and the area A2 of one half of the area of one triangle in the second large triangle. If A is the area of the large triangle, then
A1 = A/3 and A2 = A/(4×2) = A/8
where A is the area of the large triangle.
So the area of the shaded area is
S = A1 - A2 = A/3 - A/8 = A(1/3-1/8)=5A/24
The fraction representing the shaded area of the large triangle is
S/A = 5/24.
12 Dec 2017 at 11:12 pm [Comment permalink]
The right side of the top triangle is 1/2 * 1/4 of the large triangle.
The shaded part of the inside triangle is 1/3 * 1/4 of the large triangle.
1/2 * 1/4 + 1/3 * 1/4 = (1/2 + 1/3)*1/4 = 5/6 * 1/4 = 5/24
13 Dec 2017 at 12:05 am [Comment permalink]
.208333333. The shaded area can be viewed as 2 areas of one of the 4 small equilateral triangles. One area is 1/3 of the area of one of those triangles and the other area is 1/2 of the area of one of those triangles.
Therefore 1/3 + 1/2 = .83333. The ratio of .83333 and 4 = .208333333.
13 Dec 2017 at 1:06 am [Comment permalink]
5/24
Middle triangle is quarter of large triangle. Split into three the smallest shaded area is 1/12
Other triangle split into thirds. (1/3 - 1/12)/2 = 3/24 is other shaded area
3/24 + 2/24 = 5/24
13 Dec 2017 at 3:05 am [Comment permalink]
The shaded part is 5/24 of the original large triangle
13 Dec 2017 at 4:23 am [Comment permalink]
Dear Muarry,
1) If I am not mistaken, the area of the shaded triangle is 5/24 of the large triangle:
Let
- A=area of the large triangle,
- S=area of the shaded portion.
S = A/3 - (A/4/2)
S = A/3 - A/8 = A(1/3 - 1/8) = A((8-3)/24) = A*5/24.
2) If you see fit, you are more than welcome to use any of my puzzles/problems/factoids listed in my twitter account (https://twitter.com/dforouhari).
Happy Holidays,
Danesh Forouhari
13 Dec 2017 at 7:06 am [Comment permalink]
Hi Murray, Sorry to quibble, but I think the line pairs in last week's math puzzle problem were degenerate *hyperbolas* rather than parabolas. The parabola *is* obtained by intersecting a plane with a cone, but only in the case where the plane is parallel to a side of the cone and so only intersects one of the two half-cones. (The hyperbola occurs when the plane is closer to lining up with the axis and the ellipse when it comes in more sideways.)
Also, I am suspicious of your last graph in that set, as the pairs of parabolas don't look like actual hyperbolas (eg the blue ones are much too close together to even look like having asymptotes) and so I suspect that 4 really is the maximum number of intersections for two quadratics that don't have at least a partial coincidence (ie a non-constant common factor).
13 Dec 2017 at 7:22 am [Comment permalink]
a^2*3^(0.5)]/32 + a^2*3^(0.5)]/96=[5*a^2*3^(0.5)]/96
13 Dec 2017 at 12:25 pm [Comment permalink]
The Area of the Shaded portion is 5/24 of the Large Triangle.
Because; the 2nd figure has 4 identical triangles, each represents
1/4 of the area of the large triangle.
The central shaded area is 1/3 of small triangle
= 1/3 x 1/4 = 1/12 of area of large triangle.
The outer shaded area is 1/2 of small triangle
= 1/2 x 1/4 =1/8 of area of large triangle.
So the total area of shaded portion
= 1/12 + 1/8 = 5/24 of large triangle.
Back in the best of health, I hope!
Thanks for the puzzles.
13 Dec 2017 at 3:02 pm [Comment permalink]
Area of triangle = 1/4*1/2 + 1/4*1/3 = 5/24
I'm a bit confused after Murray's explanation of last time's puzzle: are we talking about parabolas or hyperbolas? My understanding is that a parabola does not have "two arms". I can imagine 4 intersection points for two (non degenerate) hyperbolas but the graphs shown are parabolas (although it looks like 4 separate equations and 4 graphs)
13 Dec 2017 at 5:10 pm [Comment permalink]
1/3rd of the first triangle when halved becomes a part of the shaded portion in the third triangle and 1/24th of the second triangle becomes the second part of the shaded part of the third triangle
Therefore 1/24 +1/6 =5/24
The shaded portion is therefore 5/24th of the large triangle.
14 Dec 2017 at 5:49 am [Comment permalink]
The answer is 5/24.
The triangle ABC is assumed to be equilateral, and G is assumed to be its centroid. Let Z denote the area
of ABC. The three triangles ABG, BGC and CGA have equal areas (a property of a triangle's centroid),
each equal to Z/3, and the shaded triangle (one of the four equal equilateral triangles with vertices A, a,
B, b, C, c (where a, b, c are the midpoints of each side of the the main triangle ABC) has its area equal to
Z/4. By the symmetry of the situation, the shaded area inside the triangle BCG is equal to 1/3 of the area
of abc, i.e., Z/12.
On the other hand, the area of the non-shaded region in triangle BCG is equal to Z/3 - Z/12 = Z/4, and
the triangle Cxa is half of that region, so that its area is equal to Z/8.
So, finally, the area of the shaded polygon inside BCG is Z/12, and the area of the non-shaded triangle
Cxa is Z/8, so that the area of the polygon CGya is equal to Z/12 + Z/8 = 5 Z/24. That is to say, the answer
to the problem is 5/24.
15 Dec 2017 at 7:55 pm [Comment permalink]
Thank you for another most interesting newsletter, and all those from the past year. Best wishes to you also for Christmas and 2018.
I'm curious about your observation "A parabola, when considered as the intersection of a plane and a cone, actually has 2 arms". I need to do some more pondering and visualisation! I can see this is true for a hyperbola, which would at some point intersect an attached inverted cone. But my understanding is that a parabola is the intersection with a plane parallel to the side of the cone, and this plane would then extend into "fresh air" after emerging from the first cone.
Something to ponder while the shops are closed!
Many thanks once again,
Best wishes,
Eamon
15 Dec 2017 at 8:02 pm [Comment permalink]
Hello friends
To solve above problem let's assume that this an equilateral triangle with side a having area √3/4a^2.
Now inner triangle will also be an equilateral triangle with side a/2.
Let's name the bigger triangle as ABC and smaller one DEF. D is opposite to A and E is opposite to B. Let's Q is midpoint of FE.
Now area of AQE is given by 1/2 QE*AE Sin60 deg.that is √3a^2/32.
Now let angles bisector of parent triangle meet at O. Let's R is mid point of ED. NOW we have to find area of EQOR WHICH will be find out by converting it into two triangles EOQ and EOR therefor area of EQOR=2area of EOQ.
EO/EQ=secant 30 deg
EO=a/4*2/√3=a/2√3
Therefore area of EQOR=2*1/2*a/4*a/2√3*sin 30deg =a^2/16√3.
Therefore area of shaded region =( √3/32+1/16√3)*a^2=(5/32√3)a^2
Hence fraction of shaded to parent triangle is
(5/32√3)a^2/(√3/4)a^2=5/24.
HENCE SHADED PORTION IS 5/24 OF ITS PARENT TRIANGLE
15 Dec 2017 at 8:03 pm [Comment permalink]
Solution to this month's puzzle:
From visual inspection we can see that the shaded area is 1/3 of the large triangle minus 1/2 of 1/4 of the large triangle = 1/3 - 1/8 = 8/24 - 3/24 = 5/24 of the large triangle.
16 Dec 2017 at 9:09 pm [Comment permalink]
Answer is 1/6
1/4-(1/4 / 3)
22 Dec 2017 at 7:20 am [Comment permalink]
Hi again. My previous comment is now redundant so please feel free to delete it. But I do have another suggestion.
In the algebraic solution it might help to mention that both equations (3) and (4) are satisfied whenever the common factor 2x+y-4 is zero and that (only) when it is not zero we need the other two factors to be zero, giving x-y=0 and 3x-y=2 (which can be solved to give x=y=1). The solution set of the two original equations is therefore just the set of all points where either 2x+y=4 (the shared line) or x=y=1 (the intersection point of the two non-shared lines). So it might be clearer to say that the solutions lie along the line y=-2x+4 or at the intersection of y=x and y=3x-2 rather than "along" all three lines (since most other points on those last two lines are actually solutions of just one but not both the given equations).
27 Dec 2017 at 12:19 am [Comment permalink]
Please draw a triangle.
First, I am assuming that the triangle is equilateral. A scalene triangle is dealt with later.
Draw a equilateral triangle ABC.
The area of triangle ABC = 12 x 12√3 = 144√3
Draw the three medians, AD, BE and CF to meet at the centroid G.
Let the length of each side of the triangle be 24 units.
Then |BD| = 12 and |AD| = 12√3 i.e. 12 by square root of 3.
[AD] is divided in the ratio 2:1.
Then |AG| = 8√3.
Triangle AGE is is a 30º, 60º, 90º triangle GE perpendicular to AE.
|GE| = 4√3 and |AE| = 12
Area of triangle AGE = 0·5 x 12 x 4√3 = 24√3
|HE| = half of |AF| = 6 and thus |GH| = 2√3
Area of triangle GEH = 6 x √3 = 6√3
Quadrilateral AGHE = 24√3 + 6 √3 = 30√3
Required fraction = 30√3 ÷ 144√3 = 5/24.
The problem can also be approached using coordinate geometry on the points A(0, 12√3), B(-12,0) and C(12,0).
Now the scalene triangle by the coordinated geometry approach.
Draw the triangle as given.
Select coordinates A(12b, 12c), B(-12a, 0), C(12a, 0). Use of 12 avoids fractions later.
The area of triangle ABC = 12a x 12c = 144ac.
Draw the three medians, AD, BE and CF to meet at the centroid G.
Coordinates of G are (4b, 4c).
Coordinates: D = (0, 0), E = ( 6a + 6b, 6c), F = (-6a + 6b, 6c).
The mid-point of DE is H = ((3a + 3b, 3c)
Area of quadrilateral GHEA with coordinates (4b, 4c), (3a + 3b, 3c), (6a+6b, 6c), (12b, 12c)
translated back to coordinates (0, 0), (3a - b, -c), (6a+2b, 2c), (8b, 8c) is 30ac.
{Get the area using two triangles}.
Triangle AGE = 24ac and triangle EGH = 6ac.
Other triangles will come out similarly.
Required fraction is then 30ac ÷ 144ac = 5/24
19 Jan 2018 at 9:59 am [Comment permalink]
Congrats to Gerard for going the extra mile to get a proof for the scalene case. Like most other solvers I just assumed the triangle was equilateral and did it by partitioning the shaded area into two parts (one being 1/2 of 1/3 of the whole thing and the other being 1/6 of 1/4 for a total of 1/6+1/24=5/24). But Gerard's proof of the general case got me thinking! ...With two conclusions:
First, the partitioning approach does still work in the scalene case, but one needs to use the facts that the lines joining feet of the medians are parallel to the sides of the triangle and so divide it into 4 congruent pieces, and that the areas of triangles from a point to equal bases on the same line are equal.
Second, and maybe more amazing, is the fact that the general case (of this and many similar problems) actually follows from the equilateral case. The key is to note that any triangle can be projected onto an equilateral one. (For an informal "proof" just draw the triangle on a piece of paper and move around until it "looks" equilateral, or hold up a small cut-out equilateral triangle in between you and the paper and tilt it around until it exactly covers your view of the triangle you drew). But the projection just multiplies all areas by the same factor - and so preserves the ratios!
20 Jan 2018 at 1:17 am [Comment permalink]
Many thanks, Alan.
There are so many ways of looking at this problem.
Regards
Gererd G.