IntMath Newsletter: Halloween, GeoGebra resource
By Murray Bourne, 31 Oct 2012
31 Oct 2012
In this Newsletter:
1. What happened to the IntMath Newsletter?
2. Math-inspired Halloween Pumpkin
3. Resource: GeoGebra Examples
4. Intmath polls
5. Math puzzles
6. Friday math movies
7. Final thought - overalls
1. What happened to the IntMath Newsletter?
It's been a while since the last edition of the IntMath Newsletter. Thank you for your patience!
I've had a very busy few months, especially now that I'm doing freelance training work. My many tasks have included:
- Training teachers (running courses and giving feedback on lesson videos)
- Training university math lecturers (mostly one-on-one feedback on lectures)
- Doing volunteer training in Cambodia (Phnom Penh and Battambang)
- Developing online mathematics courses
I'm a bit more free over the next few months so I hope to get back to writing the Newsletter more often. I've got a large number of article requests and I'm looking forward to writing them!
2. Math-inspired Halloween Pumpkin
 |
Here's a neat mathematically-generated Halloween pumpkin, developed using the Mathematica computer algebra system. You can manipulate it using the supplied CDF document. |
3. Resource: GeoGebra Examples
GeoGebra is an excellent free math exploration tool. (All schools should use it and give students interesting assignments where they learn math by making geometric constructions.)
 |
See several GeoGebra examples by Malin Christersson. Math topics that are covered include polar coordinates, functions, trigonometry, calculus and statistics. |
4. Intmath polls
The recent IntMath poll (August to October 2012) asked readers about their use of gadgets when learning math. We hear a lot about how tablets are taking over in this "post-PC" era, but not yet, based on this (very unscientific) set of results. It's interesting that the numbers of students using calculator and mobile phone are very close. With a good phone app, you don't really need a calculator.
I mostly learn math using:
Laptop: 25%
No device: 24%
Computer (desktop): 20%
Calculator: 15%
Mobile phone: 12%
Tablet (iPad etc): 4%
Total votes: 3900
Latest poll - math homework: The current poll asks readers about the amount of math homework they do per week. You can add your vote on any page in IntMath.com.
5. Math puzzles
The puzzle in the last IntMath Newsletter involved a story about Percy, Quincy and Robby. The correct answer (that Quincy gets $345) was given by Shaun, Peter Hunter, Thomas A Buckley and Dineth. As Dineth said, the puzzle had a bit of a problem, since $10 was left over and it was not clear who should get it.
Latest puzzle: A tangent at P to the smaller of 2 concentric circles intersects the outer circle at Q and R as shown. The length of QR is 14 cm. What is the shaded area?
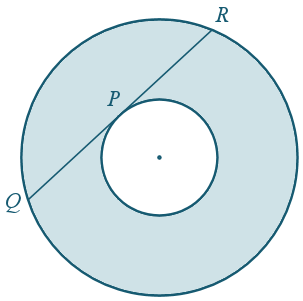
Leave your responses here.
6. Friday math movies
 |
(a) Advancing the Digital Arts Every time you see a computer graphic, you are looking at math in action. |
 |
(b) What doctors don't know about the drugs they prescribe Ben Goldacre exposes a dirty truth the drug companies don't want you to know - medical journals prefer to publish positive results. Friday math movie: What doctors don't know about the drugs they prescribe |
7. Final thought - overalls
Thomas Edison was an inspiring inventor and is well-known for his tenacity. Here are his thoughts about opportunity.
Opportunity is missed by most people because it is dressed in overalls and looks like work. [Thomas Edison]
Until next time, enjoy whatever you learn.
See the 33 Comments below.
31 Oct 2012 at 10:40 pm [Comment permalink]
5. MATH PUZZLE:
ANS: 49*pie
31 Oct 2012 at 10:41 pm [Comment permalink]
taking O as the centre as the circles,π as pi
the distance PR=PQ=7
the distance OQ=OR=y
the distance OP=x
then, OR= √(7^2+x^2 )
area of smaller circle = πr^2 = π(OP)^2 = πx^2
area of larger circle = πr^2 = π(OR)^2 = π(√(7^2+x^2))
= 49π + x^2π
area of shaded region = area of larger circle-area of smaller circle
= 49π + x^2π - πx^2
= 49π
= 154cm^2
31 Oct 2012 at 10:42 pm [Comment permalink]
taking O as the centre as the circles,? as pi
the distance PR=PQ=7
the distance OQ=OR=y
the distance OP=x
then, OR= ?(7^2+x^2 )
area of smaller circle = ?r^2 = ?(OP)^2 = ?x^2
area of larger circle = ?r^2 = ?(OR)^2 = ?(?(7^2+x^2))^2
= 49? + x^2?
area of shaded region = area of larger circle-area of smaller circle
= 49? + x^2? – ?x^2
= 49?
= 154cm^2
31 Oct 2012 at 10:47 pm [Comment permalink]
Shaded area is 153.93 cm2.
31 Oct 2012 at 11:11 pm [Comment permalink]
Assuming the radius of the inner circle is b cm (centre O), and assuming that the length of line QR is 14cm (not the arc QR), then PR is 7cm. OP is b cm, so OR is (7^2 + b^2)^(1/2).
The area of the smaller circle is pi x b^2, the area of the larger circle is pi x (7^2 + b^2), so the area of the shaded region is 49pi .
31 Oct 2012 at 11:25 pm [Comment permalink]
Call the radius of the smaller circle "x" and call the radius of the larger circle "y". Segment QR is perpendicular to the radius of the smaller circle, so you can draw a right triangle with segment QP and the radius of the smaller circle as legs. The legs have length x and 7 (half of 14) and the hypotenuse has length y. By the Pythagorean theorem, x^2+7^2=y^2. The area of the shaded region is pi*y^2-pi*x^2. By substitution, this is pi*(x^2+49)-pi*x^2. But that equals pi*x^2+49pi-pi*x^2. Therefore, the area of the shaded region is 49pi.
1 Nov 2012 at 1:11 am [Comment permalink]
we know radius and tangent are penrpendicular to each other. so radius 'r' of small circle bisects chord QR . So if 'O" is the centre OP=r, OQ= R , so by pythagorean rule PQ square = R square -- r square
So area of shaded region =49 pi
1 Nov 2012 at 1:38 am [Comment permalink]
Hi, Murray...Nice to see you back !!!!
I've been missing yours emails.
Congratulations for your new role in maths as a teacher of teachers.....
Kind regards
Bruno
1 Nov 2012 at 2:58 am [Comment permalink]
Let O be the center of the circles.
Then OR^2 = 49 +OP^2 {1}
Shaded aerea : pi.OR^2 -pi.OP^2 = pi(OR^2 -OP^2) {2}
{1} in {2} : pi(49 + OP^2 -OP^2)=49.pi = 153,93cm^2
1 Nov 2012 at 3:27 am [Comment permalink]
I make it 49 pi.
1 Nov 2012 at 12:44 pm [Comment permalink]
49*pi
1 Nov 2012 at 1:35 pm [Comment permalink]
Latest puzzle: A tangent at P to the smaller of 2 concentric circles intersects the outer circle at Q and R as shown. The length of QR is 14 cm. What is the shaded area?
Ans: 98*pi = 307.8760800517997
- Suhas
1 Nov 2012 at 1:41 pm [Comment permalink]
Correct Answer:
Latest puzzle: A tangent at P to the smaller of 2 concentric circles intersects the outer circle at Q and R as shown. The length of QR is 14 cm. What is the shaded area?
Ans: 49*pi = 153.9380400258999
- Suhas
1 Nov 2012 at 4:28 pm [Comment permalink]
r^2+7^2=R^2 --> R^2-r^2=49
pi*(R^2-r^2)=49*pi= 153.94 cm
1 Nov 2012 at 5:35 pm [Comment permalink]
49pie
1 Nov 2012 at 5:38 pm [Comment permalink]
49?
2 Nov 2012 at 2:17 am [Comment permalink]
Here is the answer to the puzzle:
Let the radius of the smaller circle be r and the radius of the larger circle R.
The Area A of the shaded doughnut is equal to the large circle's area minus the small circle's area:
A= ?R^2- ?r^2 = ?(R^2-r^2)
[PO] is the radius of the small circle which is perpendicular to the tangeant (QR).
[OR] is a radius of the large circle.
We apply the Pythagorean Theorem to OPR:
OR^2=PR^2+OP^2
? R^2= (QR/2)^2+r^2
? R^2= 7^2+r^2
? R^2= 49+r^2
Substitute R^2 with 49+r^2 in A = ?(R^2-r^2):
A = ?(R^2-r^2)
A = ?(49+r^2-r^2)
A = 49 ?
2 Nov 2012 at 2:18 am [Comment permalink]
The question marks are effectively supposed to be pi symbols.
2 Nov 2012 at 7:26 am [Comment permalink]
49 pi
2 Nov 2012 at 7:26 am [Comment permalink]
it will be 49 pi
2 Nov 2012 at 8:50 pm [Comment permalink]
Change point R to X (to avoid clash with my variable)
Let O be the centre of the circles
Angle QPO is a right angle
Join QO and PO resulting in right angled triangle QPO
Let PO = r and QO = R - the radii of the small and large circles respectively
Line QP is 7 since P bisects the tangent.
By Pythagoras: R^2 - r^2 = 49
The area of the shaded portion is PI*R^2 - PI*r^2 = PI(R^2 - r^2)
But R^2 - r^2 = 49 already established therefore
The area of the shaded portion is 49PI
3 Nov 2012 at 3:14 am [Comment permalink]
Let "a" the radius of the outer circle and "b" the radius of the inner circle. Consider a point S on the outer circle, such that QS is a diametre. Thus, QS=2*a. The QRS is a right triangle. Besides, the length RS equals to the inner circle's diametre: RS=2*b.
So, [(QR)^2]+[(RS)^2]=[(QS)^2]=> [14^2]+[(2*b)^2]=[(2*a)^2]=> (a^2)-(b^2)=49 (1).
The shaded area "E" is:
E=Eout-Ein= ?*(a^2)-?*(b^2)= ?*[(a^2)-(b^2)] (2).
From (1)&(2)=> E=49*? cm^2 = 153.86 cm^2.
3 Nov 2012 at 6:11 pm [Comment permalink]
Area = ?R2 – ?r2
= ?(R2 – r2)
But R2 = 72 + r2
Area = ?(72 + r2 – r2)
= 49 ?
= 49 x 22/7
= 154 cm2.
5 Nov 2012 at 11:32 am [Comment permalink]
The area of the shaded area =154 sq cm,by taking pi=22/7.
5 Nov 2012 at 8:53 pm [Comment permalink]
pi*49
6 Nov 2012 at 2:17 am [Comment permalink]
Answer:49*Pi square cm.
6 Nov 2012 at 6:17 pm [Comment permalink]
Change point R to X (to avoid clash with my variable)
Let O be the centre of the circles
Angle QPO is a right angle
Join QO and PO resulting in right angled triangle QPO
Let PO = r and QO = R – the radii of the small and large circles respectively
Line QP is 7 since P bisects the tangent.
By Pythagoras: R^2 – r^2 = 49
The area of the shaded portion is PI*R^2 – PI*r^2 = PI(R^2 – r^2)
But R^2 – r^2 = 49 already established therefore
The area of the shaded portion is 49PI sq cms
10 Nov 2012 at 11:00 am [Comment permalink]
The shaded area is 49Pi = 153.938cm^2.
After inspection, it appears that ANY smaller circle of radius r can have a 14 cm tangent to become a chord of a larger circle having radius R. The two radii and the half tangent (chord) length 7cm form a Right Angle Triangle. Taking any value for r then allows a corresponding value for R to be found. Noting that R is the hypotenuse.
R = SqRt( r^2 + 7^2)
Shaded area is then = Pi(R^2-r^2)cm^2.
It only remains to show that whatever the radius of the smaller circle the same area results. This indeed works out.
There is an infinite number paired circles which satisfy the problem. The area is always 49Pi cm^2
Example. Taking r as 3, then R = SqRt(3^2+7^2) = SqRt58
Shaded area = Pi(R^2-r^2) = Pi[(SqRt58)^2 - 3^2) = 49Pi
10 Nov 2012 at 11:42 am [Comment permalink]
Or, if your system can take the symbols,
R = √(r²+7²) . . Eq1
Area
= π(R²-r²)
= π((√(r²+7²))²-r²)
= π(r²+7²-r²)
= π(7²)
= 47π cm²
10 Nov 2012 at 11:51 am [Comment permalink]
Your system is ? standard Pi and SqRt symbols.
As no doubt many other useful math symbols
would also be unrecognized.
Can you have this fixed?
10 Nov 2012 at 12:17 pm [Comment permalink]
Hi Thomas.
Most blog software "chews" any unusual input, usually for security purposes. I've played with such issues before, and in fixing one thing (so math will show), you end up breaking something else (or compromising security).
You can use standard HTML entities for math, like π for π, and √ for the square root sign, √.
But if you copy from (ugh) MS Word or similar, it gets chewed.
I updated your entry to show proper symbols 🙂
14 Nov 2012 at 6:06 am [Comment permalink]
well, the distance 14 in this quiz determines the size of the required area.the varying radius of the smaller circle will give numbers for the chord diferrent from 14 and the values of the calculated area varying diferrently from 49pi. in short with this, half the chord length squared multiplied by pi will give the desired result. the radius of the smaller circle is lost in the subtraction between terms of the two cicles.
2 Jun 2014 at 6:57 pm [Comment permalink]
If we assume the inner circle is equal to the size of the earth and I am standing at point P then Q (or R) is equivalent to how far over my head this puzzle is. Algebra is twisting my melon man.