IntMath Newsletter: Vectors activity, GeoGebra 5
By Murray Bourne, 28 Nov 2014
28 Nov 2014
In this Newsletter:
1. Math in cross-wind landing vectors applet
2. GeoGebra 5 now with 3-D graphs
3. Math puzzles
4. Final thought - thank you
1. Math in cross-wind landing vectors applet
I recently updated the crosswind landing applet in the Vectors chapter, so it now runs on tablets.
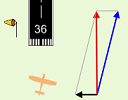 |
There is some interesting math behind this cross wind landing applet. Let's take a look at it: |
2. GeoGebra 5 now with 3-D graphs
GeoGebra is a great tool for exploring math concepts in a visual way. It is a powerful free graphing tool that allows you to develop your own interactive math applets, with no coding knowledge required (well, a little helps!).
I've been looking forward to the release of version 5 for some time, as it promised 3D graphics. It came out a few months ago and I've been having a play with it recently.
One of the early drawbacks of GeoGebra was that it worked on desktops only (being Java-based). But now it can be used on iOS, Android and Windows tablets, and as for phones, they say it's "coming soon".
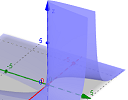 |
GeoGebra's latest version offers 3D graphs and output that can be viewed on tablet devices. Here's a quick overview with some graph examples. |
3. Math puzzles
The puzzle in the last IntMath Newsletter asked about cup capacity when mixing gasoline and oil. The correct answer with explanation was given by Chris, Rajat and Nicos.
New math puzzle: What is the value of eln x? How does it differ from the value of ln ex?
(Note: "ln" is the natural logarithm, and "ln x" means "logex". I've always thought the notation for natural logarithm is terrible, and I complain about it when introducing natural logs.)
Leave your responses here.
4. Final thought - thank you
Yesterday was Thanksgiving in the USA. In line with this topic, one of my most popular recent tweets was:
Education is a wonderful blessing, but sadly, it often seems to be appreciated only by those who don't have easy access to it.
Until next time, enjoy whatever you learn.
See the 15 Comments below.

28 Nov 2014 at 7:35 pm [Comment permalink]
Canadian Thanksgiving: the 2nd Monday in October.
You probably made the mistake to elicit feedback.
28 Nov 2014 at 7:45 pm [Comment permalink]
The two values are the same. If y=ln(e^x) then e^y=e^x (this is the definition of ln) and y=x. In the other proposition y=x.
28 Nov 2014 at 8:02 pm [Comment permalink]
e^x and ln x are inverse operations. They undo each other,
So e^ln x , e is undoing ln, and you get e^ln x = x.
Similarly, ln (e^x) = x again.
But since the function lnx does not exists for 0 and negative values of x,
e^lnx is only valid for x: }0;+inf},
as for ln (e^x) x is allowed to be negative.
e^x will always be positive.
except : lim e^x for x--->-inf the result will be 0.
Therefore ln (e^x) will be valid for x }-inf;+inf}.
28 Nov 2014 at 9:15 pm [Comment permalink]
Dear Murray
Thank you for your letter. What I would like to know if you are interested in Wind Energy, and the mathematics behind this topic, which is really highly relevant for the world of today.
Not just wind energy but solar power and the mathematics of solar cells.
28 Nov 2014 at 11:47 pm [Comment permalink]
Yes, Michael, I'm certainly interested in wind energy and sustainable energy generally. I hope to write some articles on this soon!
29 Nov 2014 at 12:17 am [Comment permalink]
e^(lnx) = x as the e^x and ln(x) are inverse of each other .
proof :- let take logarithm both side
ln(e^ln(x) ) = ln(x) [:. as e^(lnx) = x ]
=> ln(x) . ln(e) = ln (x) [:. by logarithm properties ]
hence , ln(x) = ln (x) [l.h.s = r.h.s]
It is not much differ from ln (e^x) as both comply on the rule for each others inverse .
29 Nov 2014 at 2:17 am [Comment permalink]
e^(ln(x)) = x for x>0
x has to be positive for ln(x) to exist. Therefore e^(ln(x)) is undefined for x<=0
ln(e^x) = x
e^x is always positive, therefore ln(e^x) is defined for any x.
30 Nov 2014 at 4:13 am [Comment permalink]
Let ln(e^x)=y. That means: e^y=e^x, so y=x and ln(e^x)=x (1).
From (1): ln[ln(e^x)]=ln(x). Then, e^[ln(x)]=ln(e^x)=x.
The difference is that the function f(x)=e^[ln(x)] has its domain strictly within the 1st quarter of its graph, because there are no logarithms for negative Real numbers.
There is no such a restriction in g(x)=ln(e^x) where x can be negative.
Thus, the two functions are equal only when x has positive entries: f(x)=g(x), xER+
30 Nov 2014 at 5:47 am [Comment permalink]
The answer is 1 in both cases.
I usually suggest to students that it is like digging a hole today.
Tomorrow fill it up again.
Alternately take off your sock and then put it on again.
e and ln are inverse functions.
Just like square and square root.
On most calculators both functions are on one key.
Good luck with that.
Gerry
1 Dec 2014 at 12:52 pm [Comment permalink]
e^(lnx)=ln(e^x)=x
domain(e^(lnx))=(0,+inf)
domain(ln(e^x))= real numbers
cnclusion:
domain for both functions is diffrent so above functions are not equal.
2 Dec 2014 at 1:28 pm [Comment permalink]
@Doug: Thanks! I've amended the post.
3 Dec 2014 at 3:40 am [Comment permalink]
y = e^ln(x) defines the line y = x in the first quadrant.
y = ln(e^x) defines the line y = x in the first and third.
4 Dec 2014 at 6:44 pm [Comment permalink]
I've downloaded GeoGebra and find it fascinating. But, being a novice at such things as algebra, geometry, and the like, I'll just have to delve more deeply into what the program has to offer and, be assured, it's going to take me quite a while.
4 Dec 2014 at 8:46 pm [Comment permalink]
That's great. Mike! You may find the thousands of existing GeoGebra documents in GeoGebra Tube useful.
8 Dec 2014 at 1:04 pm [Comment permalink]
Dear Mr Bourne.
In e^ln(x)let ln(x)=t.By definition e^t=x.
Thus e^ln(x)=e^t so e^ln(x)=x.
In ln(e^x)let e^x=t.
Then ln(e^x)=ln(t)
Let now ln(t)=u.By definition e^u=t.
Then e^x=e^u;implies u=x.
Therefore ln(e^x)=ln(t)=u=x
So e^ln(x)=ln(e^x).
Best regards.