GeoGebra now with 3D graphs

GeoGebra released version 5 a few months back. GeoGebra is a powerful and free graphing tool that anyone learning - or teaching - mathematics would find useful.

For me, the best feature of the new version is the ability to create 3D graphs.

When you first open GeoGebra now, you are greeted with this choice of Perspectives:

Choosing "3D Graphics", you get several new panels, which allow you to create 3D objects like a line perpendicular to a plane, a plane intersecting a cone, a plane through 3 points, a sphere, and so on:

You also get a set of empty 3-D coordinate axes, like this:

Of course, you can still create 2D graphs as before, and the interface is largely unchanged for that aspect.

Some 3D graph examples

Let's draw a few 3D surfaces using GeoGebra.

Here's a water droplet-like shape, whose equation is:

z(x, y) = 1 + 3 cos((x² + y²) 2) e^{(-(x2 + y2;))}

Next, here are some 3D graphs that were suggested by some comments on the article How to draw y^2 = x - 2?

One reader asked how to draw some graphs involving interesting asymptotes. I used some different software for those ones (which has a problem where asymptotes appear as vertical "walls" - but shouldn't be there at all.

Those graphs are similar to the following ones, which also involve an asymptote:

z = y / x²

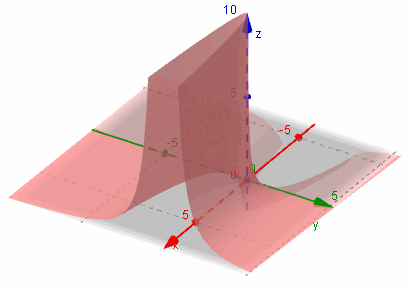
Let's consider this curve for a bit (using GeoGebra to help, of course), and investigate it from different angles.

If we fix y = 1 then the curve z = 1 / x² (it's in 2 dimensions) looks like this:

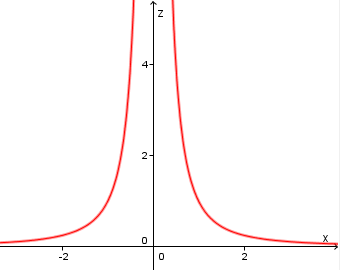
We can see this shape in our 3D graph above.

Let's now add the negative of the above graph, that is z = −y / x²

Here's what it looks like, along with our original surface:

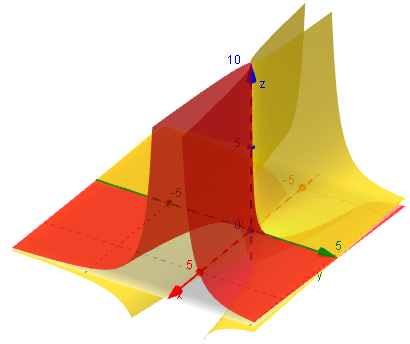
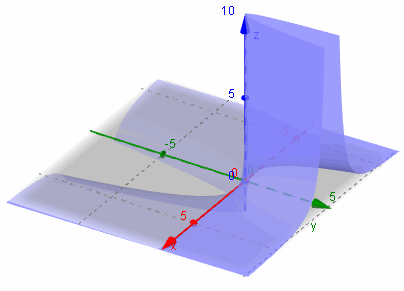
Next, we'll look at z = −x / y² by itself:

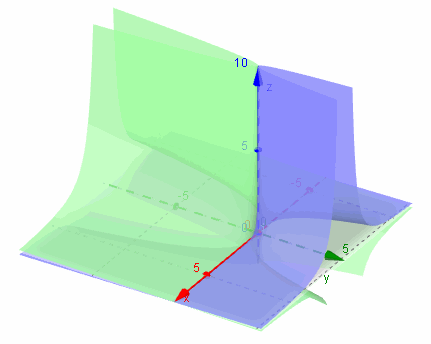
Now, we add its negative: z = −y / x² (the one in green):

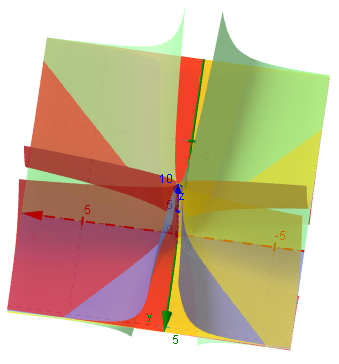
Now for all 4 surfaces together:

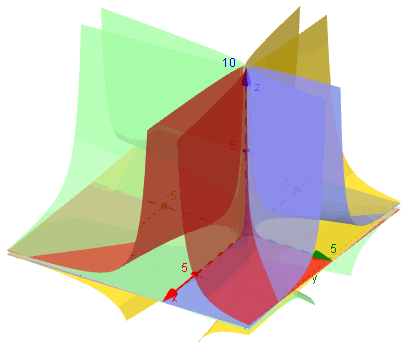
Here they are from a different point of view:

Conclusion

GeoGebra is a versatile and powerful tool. With this new version, they have addressed some of the shortfalls of earlier versions, since it now handles 3D graphs, and there are non-Java output possibilities so you can view the applets, and interact with them, on your tablet devices.

Trying to imagine surfaces in 3D really pushes your brain envelope - but this tool makes things a lot easier!

Sweet!

See the 11 Comments below.