IntMath Newsletter: How to make math interesting, GeoGebra course

7 Oct 2011

In this Newsletter:

1. How to make math class interesting
2. Trigonometry joke
3. Google computational thinking
4. Free online GeoGebra course
5. Math Puzzle: Solution and new one
6. Friday math movie: Intel Schools of Distinction winner
7. Final thought: luck

1. How to make math class interesting

Note: I wrote this article for teachers, but I would really like to hear what students think about these suggestions. Which ones would work best for you?

Reader Maria from the Philippines asked: "Pls give some tips on how to make math interesting to college students." Here are 10 ideas that are worth trying. How to make math class interesting?

2. Trigonometry Joke

This one has been doing the rounds lately. As a long-time fan of this clever actor - and of math - I appreciated it.

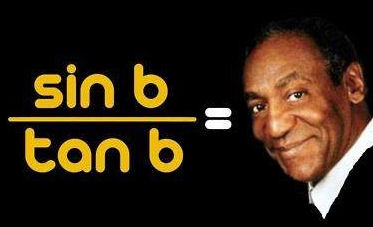
If you don't get the joke, these might help:

• Trigonometric Identities
• Bill Cosby

3. Google Computational Thinking

[Suitable for: Students who are wondering about their career path, and educators who need to advise such students.]

Many technology companies (in the West) are facing a talent vacuum, especially because fewer students are chosing the "hard" subjects like math, science and engineering. Some companies are taking their own steps to ensure they will have talented workers in the future.

In Google in Education, there is an interesting section on Exploring Computational Thinking. They explain:

Computational thinking involves a set of problem-solving skills and techniques that software engineers use to write programs that underlie the computer applications you use such as search, email, and maps.

There are various resources listed, including:

• Lessons and Examples (which includes several lessons on algebra, statistics, word problems and Python programming)
• Web Resources

Google's enthusiasm begs the question - should we teach computer programming to all students ?

Personally, I think all students should at least know the basics of how humans tell computers what to do - even if it's kept very simple.

4. Free online GeoGebra course

[Suitable for: Teachers mainly, although students will also get a lot from it.]

GeoGebra is an excellent free and open source math software. (See my GeoGebra Review).

Next week (14th to 18th Oct, 2011) there will be a free online course helping you to understand how GeoGebra can be used in your math class.

The moderator of the course is Linda Stojanovska, a GeoGebra expert. See her GeoGebra Wiki.

5. Puzzle

The puzzle in the 21 Sep IntMath Newsletter is actually a true story (well, most of it).

Julius Caesar did adopt the Julian calendar, but it was in 45 BC (not 150 BC) and it assumed a year length of 365.25 days. This was "out" by:

365.25 − 365.242218 = 0.007782 (or about 11 minutes)

It doesn't sound much, but in 1582, after a period of 45 + 1582 = 1627 years, it would be wrong by:

0.007782 × 1627 = 12.66131 days.

So the calendar had moved "out of synch" by almost 13 days.

In 1582 the seasons were coming at the wrong time and the Europeans realized they had to do something about it.

There were some other errors in the calendar, so the actual number of days that "disappeared" was 10. In 1582, Pope Gregory decreed that the 4th October would be followed immediately by 15th October.

To stop repeating the error, they decided the only century years to be leap years would be the ones divisible by 400. Thus the years 1600 and 2000 were leap years, since they are exactly divisible by 400; but 1700, 1800, and 1900 were not leap years because they are not exactly divisible by 400.

This new Gregorian calendar, which is called the "new style" (NS), was adopted much later in England on the 2nd September, 1752 (nearly 200 years later), when the error amounted to eleven days.

New puzzle

I have a number with an interesting property:

When I divide it by 2, the remainder is 1.
When I divide it by 3, the remainder is 2.
When I divide it by 4, the remainder is 3.
When I divide it by 5, the remainder is 4.
When I divide it by 6, the remainder is 5.
When I divide it by 7, the remainder is 6.
When I divide it by 8, the remainder is 7.
When I divide it by 9, the remainder is 8.
When I divide it by 10, the remainder is 9.

Find the smallest number that works.

6. Friday math movie: Intel Schools of Distinction winner

Continuing the theme of companies doing something about their impending talent shortage, here's Intel lending an educational hand.

These schools have been recognized for their contributions to math education. There are some good ideas here worth emulating. Friday math movie: Intel Schools of Distinction winner

7. Final thought – luck

The 3rd president of the US had this to say about luck. He could have been talking about exam results!

I'm a great believer in luck, and I find the harder I work the more I have of it. [Thomas Jefferson]

Until next time, enjoy whatever you learn.

See the 7 Comments below.