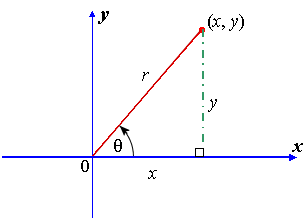Chapter Contents

• Analytic Trigonometry
• 1. Trigonometric Identities
• 2. Sin, cos tan of Sum of Two Angles
• 3. Double Angle Formulas
• 4. Half Angle Formulas
• 5. Trigonometric Equations
• 6. Express in the form R sin (θ + α)
• 7. Inverse Trigonometric Functions
• Analytic Trigonometry Problem Solver

• Comments, Questions?

Feelings about Math

Recommendation

Easy to understand trigonometry lessons on DVD. Try before you commit. More info:
MathTutorDVD.com

Online Algebra Solver

Solve your algebra problem step by step!

Online Algebra Solver »

Share

Share this page.

From the math blog...

1. Fundamental Trigonometric Identities

by M. Bourne

Before we start to prove trigonometric identities, we see where the basic identities come from.

Recall the definitions of the reciprocal trigonometric functions, csc θ, sec θ and cot θ from the trigonometric functions chapter:

Now, consider the following diagram where the point (x, y) defines an angle θ at the origin, and the distance from the origin to the point is r units:

From the diagram, we can see that the ratios sin θ and cos θ are defined as:

and

Now, we use these results to find an important definition for tan θ:

Now, also so we can conclude that:

---

Also, for the values in the diagram, we can use Pythagoras' Theorem and obtain:

y² + x² = r²

Dividing through by r² gives us:

so we obtain the important result:

sin2 θ + cos2 θ = 1

---

We now proceed to derive two other related formulas that can be used when proving trigonometric identities.

It is suggested that you remember how to find the identities, rather than try to memorise each one.

Dividing sin²θ + cos² θ = 1 through by cos²θ gives us:

so

tan2 θ + 1 = sec2 θ

---

Dividing sin²θ + cos2 θ = 1 through by sin2θ gives us:

so

1 + cot2 θ = csc2 θ

Trigonometric Identities Summary

Proving Trigonometric Identities

Suggestions...

1. Learn well the formulas given above (or at least, know how to find them quickly). The better you know the basic identities, the easier it will be to recognise what is going on in the problems.
2. Work on the most complex side and simplify it so that it has the same form as the simplest side.
3. Don't assume the identity to prove the identity. This means don't work on both sides of the equals side and try to meet in the middle. Start on one side and make it look like the other side.
4. Many of these come out quite easily if you express everything on the most complex side in terms of sine and cosine only.
5. In most examples where you see power 2 (that is, ²), it will involve using the identity sin² θ + cos² θ = 1 (or one of the other 2 formulas that we derived above).

Using these suggestions, you can simplify and prove expressions involving trigonometric identities.

Example 1:

Prove that

Answer

Example 2:

Prove that

sin y + sin y cot² y = csc y

Answer

Example 3:

Prove that

sin x cos x tan x = 1 − cos² x

Answer

Exercises

1. Prove that

tan x + cot x = sec x csc x

Answer

2. Prove that

Answer