2. Sin, Cos and Tan of Sum and Difference of Two Angles

Proof 1 - Using the Unit Circle

We start with a unit circle (which means it has radius 1), with center O.

We construct angles `BOA = alpha` and `AOP = beta` as shown.

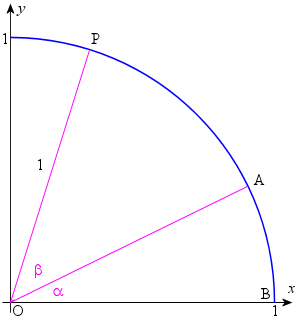
Next, we drop a perpendicular from P to the x-axis at T. Point C is the intersection of OA and PT.

We then construct line PR perpendicular to OA.

Finally, we drop a perpendicular from R to the x-axis at S, and another from R to PT at Q, as shown.

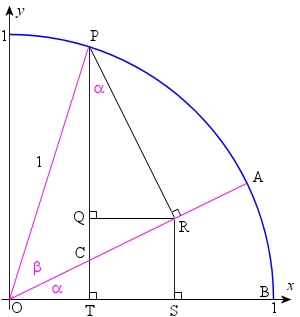
We note the following:

(1) `/_TPR = alpha` since triangles OTC and PRC are similar. (`/_OTC = /_PRC = 90°`, and `/_OCT = /_PCR = 90°- alpha`.)

(2) Length |QT| = |RS|

(3) sin (α + β) = |PT| = |PQ| + |QT| = |PQ| + |RS|

(4) |PR| = sin (β)

(5) In triangle PQR, |PQ| = |PR| cos (α)

(6) So from (4) and (5), |PQ| = sin (β) cos (α).

(7) |OR| = cos (β)

(8) In triangle OSR, |RS| = |OR| sin (α)

(9) So from (7) and (8), |RS| = cos (β) sin (α)

(10) Thus from (3), (6) and (9), we have proved:

sin (α + β) = sin (β) cos (α) + cos (β) sin (α)

Rearranging gives:

sin (α + β) = sin (α) cos (β) + cos (α) sin (β)

(11) From Even and Odd Functions, we have: cos (−β) = cos( β) and sin (−β) = −sin(β)

(12) So replacing β with (−β), the identity in (10) becomes

sin (α − β) = sin α cos β − cos α sin β

[Thank you to David McIntosh for providing the outline of the above proof.]

The Cosine Proofs

We now need to prove

cos (α + β) = cos α cos β − sin α sin β

(13) |OT| = cos (α + β)

(14) In triangle ORS, we have: `cos alpha = |OS|/|OR|`.

(15) cos (β) = |OR|, from (7) above.

(16) From (14) and (15), we obtain `cos alpha cos beta= |OS|/|OR|xx|OR| = |OS|`.

(17) In triangle QPR, we have `sin alpha = |QR|/|PR|`.

(18) sin (β) = |PR|, from (4) above.

(19) From (17) and (18), we obtain `sin alpha sin beta= |QR|/|PR|xx|PR| = |QR|`.

(20) Now |OS| − |QR| = |OT|.

(21) So `cos alpha cos beta - sin alpha sin beta` ` = cos(alpha+beta)`.

(22) Rearranging, we have:

cos (α + β) = cos α cos β − sin α sin β

(23) Once again, we replace β with (−β), and the identity in (22) becomes:

cos (α − β) = cos α cos β + sin α sin β

Proof 2 - Using the Unit Circle

We will prove the cosine of the sum of two angles identity first, and then show that this result can be extended to all the other identities given.

cos (α+β) = cos α cos β − sin α sin β

We draw a circle with radius 1 unit, with point P on the circumference at (1, 0).

We draw an angle α from the centre with terminal point Q at (cos α, sin α), as shown. [Q is (cos α, sin α) because the hypotenuse is 1 unit.]

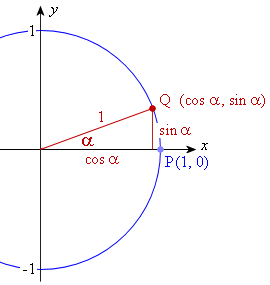
We extend this idea by drawing:

a. The angle β with terminal points at Q (cos α, sin α) and R (cos (α + β), sin (α + β))

b. The angle −β with terminal point at S (cos (−β), sin (−β))

c. The lines PR and QS, which are equivalent in length.

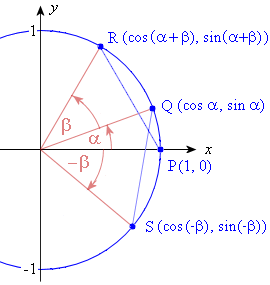
Now, using the distance formula from Analytical Geometry, we have:

PR² = (cos (α + β) − 1)² + sin²(α + β)

= cos²(α + β) − 2 cos (α + β) + 1 + sin²(α + β)

= 2 − 2cos (α + β)

[since sin²(α + β) + cos²(α + β) = 1]

Now using the distance formula on distance QS:

QS² = (cos α − cos (−β))² + (sin α − sin (−β))²

= cos² α − 2 cos α cos(−β) + cos²(−β) + sin ²α − 2sin α sin(−β) + sin²(−β)

= 2 − 2cos α cos(−β) − 2sin α sin(−β)

[since

sin²α + cos²α = 1 and

sin²(−β) + cos²(−β) = 1]

= 2 − 2cos α cos β + 2sin α sin β

[since

cos(−β) = cos β (cosine is an even function) and

sin(−β) = −sinβ (sine is an odd function − see Even and Odd Functions)]

Since PR = QS, we can equate the 2 distances we just found:

2 − 2cos (α + β) = 2 − 2cos α cos β + 2sin α sin β

Subtracting 2 from both sides and dividing throughout by −2, we obtain:

cos (α + β) = cos α cos β − sin α sin β

If we replace β with (−β), this identity becomes:

cos (α − β) = cos α cos β + sin α sin β

[since cos(−β) = cos β and sin(−β) = −sinβ]

Sine of the Sum of Two Angles

We aim to prove that

sin (α + β) = sin α cos β + cos α sin β

Recall that (see phase shift)

sin (θ) = cos (π/2− θ)

If θ = α + β, then we have:

sin (α + β)

= cos [π/2 − (α + β)]

= cos [π/2 − α − β)]

Next, we re-group the angles inside the cosine term, since we need this for the rest of the proof:

cos [π/2 − α − β)] = cos [(π/2 − α) − β]

Using the cosine of the difference of 2 angles identity that we just found above [which said

cos (α − β) = cos α cos β + sin α sin β],

we have:

cos [(π/2 − α) − β]

= cos (π/2 − α) cos (β) + sin (π/2 − α) sin (β)

= sin α cos β + cos α sin β

[Since cos (π/2 − α) = sin α; and sin (π/2 − α) = cos α]

Therefore:

sin (α + β) = sin α cos β + cos α sin β

Replacing β with (−β), this identity becomes (because of Even and Odd Functions):

sin (α − β) = sin α cos β − cos α sin β

We have proved the 4 identities involving sine and cosine of the sum and difference of two angles.

Summary:

sin (α + β) = sin α cos β + cos α sin β

sin (α − β) = sin α cos β − cos α sin β

cos (α+β) = cos α cos β − sin α sin β

cos (α − β) = cos α cos β + sin α sin β

Proof 3 - Using Complex Numbers

The exponential and polar forms of a complex number provide an easy way to prove the fundamental trigonometric identities.

Assume we have 2 complex numbers which we write as:

r₁e^jα = r₁(cos α + j sin α)

and

r₂e^jβ = r₂(cos β + j sin β)

We multiply these complex numbers together.

Multiplying the left hand sides:

r₁e^jα × r₂e^jβ = r₁r₂e^j(α+β)

We can write this answer as:

r₁r₂e^j(α+β) = r₁r₂(cos (α+β) + j sin (α+β)) ... (1)

Multiplying the right hand sides:

r₁(cos α + j sin α) × r₂(cos β + j sin β)

= r₁ r₂(cos α cos β + j cos α sin β + j sin α cos β − sin α sin β)

= r₁ r₂(cos α cos β − sin α sin β + j (cos α sin β + sin α cos β)) .... (2)

[since j² = −1]

Now, equating (1) and (2) and dividing both parts by r₁ r₂:

cos (α+β) + j sin (α+β) = cos α cos β − sin α sin β + j (cos α sin β + sin α cos β)

Equating the real parts gives:

cos (α+β) = cos α cos β − sin α sin β

Equating the imaginary parts gives:

sin (α+β) = sin α cos β + cos α sin β

We would then proceed to replace β with (−β) as before, to obtain the identities for sin (α − β) and cos (α − β).

Case: `tan(alpha+beta)`

Recall that

`tan theta=(sin theta)/(cos theta)`

So, letting θ = α + β, and expanding using our new sine and cosine identities, we have:

`tan(alpha+beta)` `=(sin(alpha+beta))/(cos(alpha+beta))` `=(sin alpha cos beta+cos alpha sin beta)/(cos alpha cos beta-sin alpha sin beta)`

Dividing numerator and denominator by cos α cos β:

`=(sin alpha cos beta+cos alpha sin beta)/(cos alpha cos beta-sin alpha sin beta)` `-:(cos alpha cos beta)/(cos alpha cos beta`

Simplifying gives us:

`tan(alpha+beta)=` `(tan alpha+tan beta)/(1-tan alpha\ tan beta)`

Case: `tan(alpha-beta)`

Replacing β with (−β) gives us

`tan(alpha-beta)=` `(tan alpha-tan beta)/(1+tan alpha\ tan beta)`

[The tangent function is odd, so tan(−β) = − tan β]

We have proved the two tangent of the sum and difference of two angles identities:

`tan(alpha+beta)=` `(tan alpha+tan beta)/(1-tan alpha\ tan beta)`

`tan(alpha-beta)=` `(tan alpha-tan beta)/(1+tan alpha\ tan beta)`

Recall the 30-60 and 45-45 triangles from Values of Trigonometric Functions:

We use the exact sine and cosine ratios from the triangles to answer the question as follows:

This is the exact value for cos 75^o.

We use

sin(α − β) = sin α cos β − cos α sin β

We firstly need to find `cos α` and `sin β`.

If `sin α = 4/5`, then we can draw a triangle and find the value of the unknown side using Pythagoras' Theorem (in this case, 3):

We do the same thing for `cos β = 12/13`, and we obtain the following triangle.

Note 1: We are using the positive value `12/13` to calculate the required reference angle relating to `beta`.

Note 2: The sine ratio is positive in both Quadrant I and Quadrant II.

Note 3: We have used Pythagoras' Theorem to find the unknown side, 5.

Now for the unknown ratios in the question:

`cos α = 3/5 `

(positive because in quadrant I)

`sin β = 5/13`

(positive because in quadrant II)

We are now ready to find the required value, sin(α − β):

This is the exact value for sin(α − β).

Once again, we use the 30^o-60^o and 45^o-45^o triangles to find the exact value.

In this case, for the cosine of the difference of two angles, we have:

We recognise this expression as the right hand side of:

cos(α − β) = cos α cos β + cos α cos β,

with α = x + y and β = y.

We can now write this in terms of cos(α − β) as follows:

cos(x + y)cos y + sin(x + y)sin y

= cos[(x + y) − (y)]

= cos x

We have reduced the expression to a single term.

We recall the 30-60 triangle from before (in Values of Trigonometric Functions):

Using

cos(α + β) = cos α cos β − sin α sin β

and our 30-60 triangle, we start with the left hand side (LHS) and obtain:

Since the LHS = RHS, we have proved the identity.