IntMath Newsletter: hyperbolas, Pixar, PhotoMath
By Murray Bourne, 25 Nov 2016
25 Nov 2016
In this Newsletter:
1. Interactive hyperbola graphs
2. Pixar in a box
3. Resource: PhotoMath
4. Math movie: Teach for Mastery
5. Math puzzles
6. Final thought: beliefs
0. Gratitude
It's the season for giving thanks, so here goes. For me, the greatest thing to be grateful for is my well-rounded and fair education. It was very sad to read about the children of Mosul who were being indoctrinated with a corrupted curriculum while ISIS was in charge. Most kids stayed away, being denied a vital education.
On with the Newsletter.
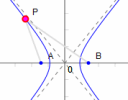
1. Interactive hyperbola graphs
 |
This page has 4 different hyperbola graphs where you can explore the characteristics, such as what is meant by "path traced out by a point where the difference of the distances from 2 fixed points is a constant." A picture is worth a thousand words! See: |
2. Pixar in a box
There are a lot of interesting applications of mathematics to learn from Pixar in a Box. From the Khan Academy site:
Pixar in a Box is a behind-the-scenes look at how Pixar artists do their jobs. You will be able to animate bouncing balls, build a swarm of robots, and make virtual fireworks explode. The subjects you learn in school — math, science, computer science, and humanities — are used every day to create amazing movies at Pixar.
 |
In the Effects section, we learn how "artists create explosions, fire, and water by breaking them down into millions of tiny particles and controlling them using computer programming." |
3. Resource: PhotoMath
 |
PhotoMath is a clever iOS and Android app. You point your camera at an algebra question and it will solve it for you, including giving you the steps. It reads (neat) handwriting, and in my tests, was able to handle questions involving integrals, square roots and trigonometry. |
Search for PhotoMath on your phone or tablet in the App Store or Play Store. It's free until the end of November.
Disclaimer 1: IntMath has no connection with PhotoMath.
Disclaimer 2: PhotoMath, like all such computer-based math solving tools, should only be used to check your own work (which helps you to learn) - NOT to simply solve the homework for you (which usually results in your never knowing it).
4. Math movie: Salman Khan - Teach for Mastery
I once taught a class of pre-service primary school teachers. Many of them were not at all confident in mathematics generally, and certainly not at the level they were going to be teaching (decimals, fractions, money, units and so on).
I decided to use a mastery testing approach with this class. Students were given a series of quizzes throughout the semester, and they needed to obtain 80% to pass each one, and couldn't go on until they had "mastered" the earlier ones. They were given as many attempts as they needed. The test questions were taken from Year 5 and Year 6 primary school mathematics text books. While many students were initially unhappy about having to go through such a process, by the end of the semester they could see the point, and were much more confident (and competent) in the math they they would teach in the future.
 |
This TED talk brought back strong memories of those wanna-be primary school student teachers. Salman Khan argues rightly that too often we allow math students to move on to the next level when many are not ready, guaranteeing frustration, boredom, and hatred for the subject. |
5. Math puzzles
The puzzle in the last IntMath Newsletter asked about the length of rope needed to allow a sheep to eat half of a circular pen of grass.
There was one correct solution and it was well done by Gerard. (I added some images so Gerard's answer would be easier for you to follow.) There was no "nice" algebraic way to solve the final equation involving an angle (which had the variable both inside and outside trigonometry expressions). Two methods are shown: (1) Solving by Newton's Method, and (2) Solving graphically.
New math puzzle
If the number ABC is written "in decimal form", it means it has value A × 100 + B × 10 + C × 1.
Given that identical letters stand for identical digits, and different letters are different digits, what are A, B and C if the following numbers are written in decimal form and:
ABC + AB + A = 300?
You can leave your responses here.
6. Final thought: beliefs
Considering Trump's astonishing announcements that he's appointed Stephen K. Bannon (former manager of the right wing Breitbart News) as a strategist, and that he's going to kill NASA's climate research budget, it's worth contemplating Voltaire's statement:
Those who can make you believe absurdities can make you commit atrocities. [Voltaire, 1694-1778]
Until next time, enjoy whatever you learn.
See the 32 Comments below.
25 Nov 2016 at 7:01 pm [Comment permalink]
A=2
B=7
C=1
A+B+C=10
B+A+1=10
A+1=3
Just solve A then B and finally C so
271+27+1=300
25 Nov 2016 at 7:45 pm [Comment permalink]
Sir,
Ans: A=2, B=7, C=1
Explanation:
ABC+AB+A = 300
we can also write it as AAA+BB+C = 300 -- (i)
by following logic based on fundamental summation procedure
1) A+B+C=10*x
2) A+B+x = 10*y
3) A+y=3
therefore, A>1 --(iii)
therefore, A=2
then BB+C = 300-222 = 78 -> B=7, C=1
25 Nov 2016 at 8:58 pm [Comment permalink]
271+27+2=300
100A+10B+C+10A+B+A=300
111A+11B+C=300
MAXIMUM{A}=2, because: A=(300-11B-C)/111<300/11<3
If A = 1, then: 11B+C = 189, but MAXIMUM{11b+c}=99+9=108, because:
b,c < 10.
therefore: A = 2, then:
11B+C=78
B=(78-C)11<78/11<8, therefore B<8
also: C78-10=68, B>68/11>6, therefore B=7, then:
C=78-77=1
A = 2, B = 7, C = 1
25 Nov 2016 at 9:01 pm [Comment permalink]
Working from the given observation that A × 100 + B × 10 + C × 1, we can state that
111 * A + 11 * B + C = 300
Clearly A cannot be greater or less than 2
111 * 2 + 11 * B + C = 300
11 * B + C = 300 - 222
11 * B + C = 78 Where B cannot be greater than 7. If C is to be a single digit, B can also be no less than 7.
11 * 7 + C = 78
This results in C = 1
A = 2, B = 7, C = 1
25 Nov 2016 at 9:15 pm [Comment permalink]
Given: ABC + AB + A = 300
Rewrite in decimal form:
100A + 10B + C + 10A + B + A = 300 or 111A + 11B + C = 300
Assuming that we are dealing only with positive integers, then A must be 2; substituting we then would have 222 + 11B + C = 300 or
11B + C = 78. B must equal 7 (if larger, then C would be negative, if smaller, then C would be a two digit number which isn't allowed). Then C = 1.
Summary: A= 2, B=7, C=1
25 Nov 2016 at 11:35 pm [Comment permalink]
ABC
..AB
+..A
------
300
A=1 or A=2
If A=1 ; carry must be 2, which is impossible since C+B+A<20
So A=2 ; carry=1 ; B+2+1=10 ;B=7
And C+7+2=10 ; C=1
solution: A=2;B=7;C=1
281+27+2=300
25 Nov 2016 at 11:59 pm [Comment permalink]
Solution to puzzle
ABC+AB+A=300
Therefore 100A+10B+C+10A+B+A=300
Collecting terms, 111A+11B+C=300
A must be equal to 1 or 2, otherwise total would exceed 300
If A=1 then 11B+C=300-111=189
This has no solutions for B & C between 1 and 9. Therefore A=2
Hence 11B+C=300-222=78
This has a solution B=7 and C=1
Hence A=2, B=7, C=1
Check: ABC+AB+A = 271+27+2=300
26 Nov 2016 at 12:21 am [Comment permalink]
This is in reference to item 6 (Final thought: beliefs) of the latest IntMath e-mail: Stay out of politics with this newsletter. It is supposed to be for math only. I resent you trying to influence my political beliefs and imply that I can be duped to commit atrocities.
26 Nov 2016 at 12:31 am [Comment permalink]
@Henri: Trump said during his campaign he would re-introduce torture.
I do not apologise for inviting people to think carefully about the world-wide implications of a Trump presidency.
26 Nov 2016 at 12:40 am [Comment permalink]
Maths might be an abstract subject, but there is nothing to exclude human opinion and experience in a newsletter. Murray is perfectly entitled to make a gentle comment about current events. There is nothing controversial in stating that Trump is controversial - controversy is part of his continued self referencing.
26 Nov 2016 at 12:49 am [Comment permalink]
A=1 or 2
C,B= 0.,1,...,9.
111A+11B+C=300
A=2
B=7
C=1
26 Nov 2016 at 1:12 am [Comment permalink]
A+B+C=10 (write 0, carry 1)
A+B=9 (total 10, write 0, carry 1
A=2 (total 3)
So, A=2, B=7, C=1
26 Nov 2016 at 4:32 am [Comment permalink]
PhotoMath is a great app for students to cheat on math tests with their cell phone. You should not be publicizing this app.
26 Nov 2016 at 4:40 am [Comment permalink]
@Forrest: I agree with your sentiments, but can there are already many similar products out there which can be used to help learning.
I have amended the post and added a second disclaimer (which I should have had in the first place). Thanks for pointing it out!
26 Nov 2016 at 4:49 am [Comment permalink]
A=2 B=7 C=1
26 Nov 2016 at 5:53 am [Comment permalink]
A cannot be 0 or 3, since the sum is 300.
So A is either 1 or 2.
C+B+A must be 10 (zero ones in 300).
B+A must be 9 (tens) (zero tens in 300).
If A = 1, then B = 8, which makes C = 1 also – not allowed.
If A = 2, then B = 7, which means C = 1.
SOLUTION: 271 + 27 + 2 = 300
26 Nov 2016 at 9:46 am [Comment permalink]
This was easy...
271 + 27 + 2 = 300
26 Nov 2016 at 11:47 am [Comment permalink]
Expanding the given equation gives
111*A+11*B+C=300
This can be solved by simple iteration or a computer program.
This gives the answer as A=2, B=7, C=1
27 Nov 2016 at 1:24 am [Comment permalink]
Hello Murray,
Loved the Pixar in a Box, have sent it to many friends. Kind regards, Roger
27 Nov 2016 at 8:56 am [Comment permalink]
While reading your final thought it occurred to me that Mr. Trump is a business person. What kind of data is he willing to accept? What kind of data does he trust? What sources does he look to and when does he look? What kinds of risk is he unwilling to take?
If we who understand that climate change is real can start putting the facts and the risks in front of him in a place he will read them and in a way that encourages him to trust them, then we might have a chance of bringing him on board and getting his help. It should be remembered that the EPA was instituted by a Republican, Richard Nixon. There is always hope.
Thanks for the excellent newsletters.
Francis Kisner
27 Nov 2016 at 9:46 pm [Comment permalink]
Hello Murray , The solution of the puzzle is A=2 , B = 7 , C = 1
......................
If the number ABC is written "in decimal form", it means it has value A × 100 + B × 10 + C × 1.
Given that identical letters stand for identical digits, and different letters are different digits, what are A, B and C if the following numbers are written in decimal form and:
ABC + AB + A = 300?
..........
Is this true solution
28 Nov 2016 at 8:18 am [Comment permalink]
The answer is A=2, B=7, and C=1,
because from:-
ABC + AB + A = 300
(100A +10B +C) + (10A+B) + A =300
111A + 11B + C = 300
By examination, 2 is a likely substitute for A, so;
(222) +11B + C =300,
Again by examination 7 is a likely substitute for B, so;
222 + 77 + C = 300. So C = 1
Proof check
(2x100 + 7x10 + 1x1) + (2x10 +7x1) + 2x1 =300
So A=2, B=7, and C=1
Solutions by the Power of Number Crunching.
29 Nov 2016 at 1:17 am [Comment permalink]
271 + 27 + 2 = 300
29 Nov 2016 at 8:37 pm [Comment permalink]
Hello Murray
ABC ,DEF ARE TWO TRIANGLES , AB = DE, AC =DF, THE MEASURE OF THE ANGLE BAC > THE MEASURE OF THE ANGLE EDF . PROVE THAT BC > EF ( BY 2 DIFFERENT METHODS)
30 Nov 2016 at 6:36 am [Comment permalink]
Re: 6. Final thoughts: beliefs
That quote cuts both ways...
Whether climate change, brexit, gun control/rights, insert your own topic, if you follow the money, you will find selfish actors on both sides that seek to obfuscate the truth and push their own agendas of profit...
30 Nov 2016 at 8:17 am [Comment permalink]
@Karam: Please ask such math questions in the IntMath Forum.
30 Nov 2016 at 12:53 pm [Comment permalink]
Apologies if I'm misinterpreting the question; I'm new
A = 2, B = 7, C = 1?
ABC + AB + A
271 + 27 + 2 = 300
1 Dec 2016 at 3:38 am [Comment permalink]
We must assume that A, B and C are all natural numbers between 1 and 9 inclusive.
Start with
100 A + 10 B + C + 10A + B + A = 300
That is
111A + 11B + C = 300
Rearrange:
C = 300 - 111A - 11B
If A = 3 then C = 300 - 333 - 11B which is negative.
Then A must be less than 3 or A = 1 to A = 2.
If A = 1 then C = 300 -111 - 11B = 189 - 11B
Therefore 189 - 11B > 0
11B < 189
B 0
11B < 78
B < 7·90909.. < 8
If B = 7 then C = 78 - 77 = 1 which looks good.
If B = 6 then C = 78 - 66 = 12 which is not less than 9
and any other value for B less than 6 would make C larger.
Then B must be greater than 6 and so B = 7
Then A = 2, B = 7 and C = 1
Check
271 + 27 + 2 = 300.
Maybe the Diophantine equation could be solved by ancient methods but lief is too short for that.
4 Dec 2016 at 4:40 am [Comment permalink]
For the math puzzle:
, 
, 
.
The original sum works out to
.
Since B and C are single digits, the maximum value of
is 
. And 
. So 111A has to be equal to at least 192. The least value of the sum 11B + C is 0, and now we have 
. The only integer solution for this inequality is 2, and therefore 
.
Now
, so 
. In a similar process, C is on the interval ![[0, 9]](https://www.intmath.com/images/img_tex2png/intmath-newsletter-hyperbolas-pixar-photomath-11048_1653.png)
, so 
, and the only possible integer solution is 
.
Finally,
, and 
.
I liked your puzzle.
5 Dec 2016 at 9:38 pm [Comment permalink]
A lie told often enough become the truth. Unknown
18 Dec 2016 at 10:58 pm [Comment permalink]
ABC-271, AB-27, A-2
The sum of these three would add up to 300.
22 Dec 2016 at 7:29 pm [Comment permalink]
271+27+2=300