Math tests and rice paddies

I performed an interesting experiment today. I got a Chinese friend to count frantically from 1 to 10 repeatedly while I did the same in English.

Why?

Outliers

I enjoyed reading Malcolm Gladwell's (rather politically incorrect) Outliers.

He argues in the book that "genius" and "success" are due to good luck, just as much as they are due to hard work or good management.

The term "outlier" comes from the field of statistics. It is common when we measure things (like height or weight of people) to find the observations tend to cluster near the average (or "mean") and so we get the familiar bell-shaped curve.

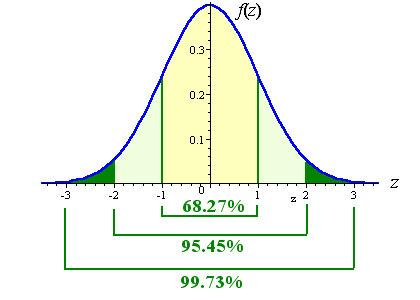
The different colors indicate the number of standard deviations we are from the average. The middle (yellow) portion is within ±1 standard deviation from the mean (representing just over 68% of the observations), the light green section represents ±2 standarad deviations (around 95.5% of the observations) and by the time we are ±3 standard deviations out, we have nailed just about all the observations (99.7%). ("Standard deviation" is an indicator of how spread out the observations are.)

An "outlier" is a result that sits outside these "normal" limits. There is nearly always someone who is much shorter than everyone else, or someone who is much taller.

Back to the book

Gladwell is an entertaining writer and includes many stories to illustrate his points.

He cites examples of extraordinarily successful people (like the Beatles, and Bill Gates) who not only worked hard, but were extremely fortunate to have been born at just the right time and place. Change one of the important inputs to their lives, and things would have been very different.

He talks about the notion that to become an "expert", we need to put in 10,000 hours work in that field. It turns out the Beatles put in around about that amount of time practicing in seedy bars in Hamburg, Germany before hitting the big time in the early 1960s.

Bill Gates programmed his life away for countless hours (somewhere around 10,000 of them) before setting up his software company.

Math tests and rice paddies

In Outliers, Gladwell describes 2 reasons why he believes Asians are better at math than anyone else in the world:

1. They have descendants who worked extremely long hours in rice paddies (and many still do), so they absorbed important concepts like "tenacity" and "perseverance"
2. They have a linguistic advantage, since Asian numbers are better organized than in European languages, and they are easier to say.

I agree there are cultural differences that explain Asian's better math scores. Certainly Asian parents are more interested in how their children are going in school compared to Western parents, and they tend to push their children. There is also a positive view in society towards science and engineering, and mathematics in particular.

But what about that linguistic advantage?

Certainly Chinese (and Japanese and Korean) numbers are more logical than English numbers.

Consider "eleven". That word has no connection with its numerical components, "ten" or "one". ("Eleven" actually means "one left".)

But in Chinese (and Japanese), we write 十一 for the number 11. The first character (looking like a plus sign) is "ten" and the second (looking like a minus sign) is "one". The number, as written, means "10 plus one" and is pronounced "shi yee" in Chinese and "juu ichi" in Japanese. In both cases, it means "ten (plus) one". So the name of the number describes perfectly the value of the number.

"Twelve" is written 十二 (meaning "10 plus 2"). The second character, with 2 strokes looking like an equal sign, is the number 2.

This pattern of adding on to "ten" is is continued up to 19. So we have:

10: 十

11: 十一

12: 十二

13: 十三

14: 十四

15: 十五

16: 十六

17: 十七

18: 十八

19: 十九

Then we have 二十. This is "two (times) ten", pronounced "er shi" (in Chinese) and "ni juu" in Japanese. Once again, the number's name describes the value.

I think you'll agree the numbering (and naming) system is quite logical, more so than most European numbering systems.

What does the English word "twenty" actually mean? Apart from the first 2 letters, it seems to have little to do with its value. (It actually comes from Old English meaning "two groups of 10". But the word is over 1,000 years old and we no longer really understand it.)

What does it all mean?

When the names of numbers relate closely to the value of those numbers, it is easier to understand those numbers and mathematics involving those numbers. It means Asian school kids have a distinct advantage, and they can learn larger numbers compared to Western children, at an earlier age.

These are the kinds of "opportunities" Gladwell points out throughout his book — the ones that increase the chances of greater success (or greater misfortune) through "happy" accidents of time, place or culture.

The counting experiment

One of the things Gladwell claims for the superiority of Asian math is that it takes a lot longer to say English numbers than Chinese numbers. This will have an effect on how quickly we can do math.

I had some doubts about that since "one", "two" and "three" were all mono-syllabic, and the only number less than 10 that has 2 syllables is "seven". Surely it would take about the same time to say the Chinese "yi", "er", "san", "si", ..., as it would to say the English "one", "two", "three", most of which are also mono-syllabic?

So I got my friend to count as fast as she could from 1 to 10 in Chinese (3 times) while I counted 1 to 10 in English (also 3 times).

In each trial, she beat me by at least 4 or 5 numbers (about 16% faster) and in her fastest run, she was a whole 10 digits ahead of me (33% faster).

She believed this was due to the fact we English speakers need to change our mouth shape more while pronouncing the numbers in English, compared to Chinese speakers saying numbers in Chinese. Could be.

So I admitted defeat and after this (very unscientific) experiment, I concluded that yes, there might be something in the differences in speed of speaking Chinese and English numbers.

Conclusion

Try to read Gladwell's Outliers. It's an interesting book. I also enjoyed his Tipping Point and Blink.

See the 5 Comments below.