Intmath Newsletter - Tests, rice, Gamma and Poisson
By Murray Bourne, 21 Apr 2010
21 April 2010
In this Newsletter:
1. Math tests and Rice Paddies
2. Tanzalin Method for easier Integration by Parts
3. Factorials and the Gamma Function
4. Maximum value of a Poisson Distribution
5. IntMath Poll result - Who are you?
6. Current IntMath Poll
7. Also on the Math Blog
8. Final thought – KIPP and opportunities
Hello everyone. Because of the wide range of readers of the IntMath Newsletter, I usually choose topics that are appropriate for anyone with a basic math understanding.
However, this Newsletter includes some more advanced topics, as requested by many readers. I have added a "suitable for" statement so you can choose the most relevant ones.
1. Math tests and Rice Paddies
Suitable for: Everyone!
 |
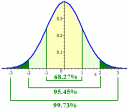Why do Asians perform so well at math? And, why are some people much more successful than others? See more at: |
2. Math tip - Tanzalin Method for easier Integration by Parts
Suitable for: Those who have studied Integration by Parts (a calculus topic).
 |
Getting lost doing Integration by Parts? Tanzalin Method is an easier way to write the steps. See more at: |
3. The Gamma Function
Suitable for: The first part of this article is for everyone. The second part involves some calculus, but most of you will still be able to follow it.
 |
Factorials come up all the time in math, especially in probability. To calculate a factorial, all you have to do is multiply the number given by all the whole numbers less than it. So for example, "5 factorial" (written with an exclamation mark, !) is calculated as follows: 5! = 5 × 4 × 3 × 2 × 1 = 120 But factorial is only defined for whole numbers. What if we need to find 3.5 factorial? Our calculator gives us an error. Can it be done? Find out more in: |
4. Maximum value of a Poisson Distribution
Suitable for: Those who have studied Probability theory and Calculus.
 |
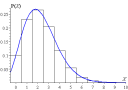A reader asked, "Can we find the maximum value of the Poisson Distribution using differentiation?" Find out more in: |
5. IntMath Poll result - Who are You?
The Mar-Apr 2010 IntMath Poll revealed around 73% of visitors to the IntMath.com are students. It's interesting that 16% of visitors are there not because they have to be, but because they are interested in math for its own sake. I knew there is a significant group of retiree readers, since many of them write to me.
The question and responses were:
Who are you?
I'm a math student: 73%
I'm a math instructor: 11%
I'm just looking: 10%
I'm retired and I want to keep learning: 6%
Total votes: 2800
Welcome, everyone!
6. Latest IntMath Poll - Why are you here?
A new poll is up and asks readers whether they are visiting IntMath because they are studying for an exam, doing homework or perhaps for some other reason.
You can respond on any page in IntMath.com.
7. Also on the Math Blog
 |
Photosynth is a great way to present photos. Behind the scenes there is an incredible amount of math going on - optimizing the photos, stitching the 3-D panoramas together and creating smooth zooms. The video is from the excellent TED series. |
8. Final thought – KIPP and opportunities
I enjoyed reading Malcom Gladwell's Outliers, the Story of Success, which examines the reasons why some people are very successful.
For me, the take-home message from the book was the importance of what people do with their opportunities.
In the many examples used by Gladwell to illustrate his points, we can see the success (or failure) of people depends very much on what they do with the cards they have been dealt.
One of Gladwell's examples was the KIPP charter schools in the US. KIPP stands for "Knowledge is Power Program". (Charter schools are funded by the government, but have more freedom to set their own agendas compared to normal schools.)
By all accounts, the KIPP approach is tough.
KIPP schools feature a long school day, an extended school
year, selective teacher hiring, strict behavior norms and a focus on traditional reading and math skills. [NBER Working Paper 15740]
Tough it might be, but the outcomes are impressive. Math and reading scores are clearly better than surrounding schools and the proportion of students qualifying for college is much higher than average.
KIPP is aimed at lower socio-economic regions, so the results are particularly dramatic. There is a long list of people trying to get into the KIPP (they use a lottery system to determine entry, not an entrance test as you might expect.)
Of course, there is much more to "success" in education than test scores, and more reasons for that success than any one school system.
However, there is a lot to be said for longer school days and a longer school year. A lower dropout rate and people fulfilling their potential are hugely important outcomes. KIPP students are being given an extraordinary opportunity to break out of the poverty and under-educated spirals. It reminds me of the brilliant work of math teacher Jaime Escalante, of Stand and Deliver fame, who sadly died recently.
Any of you attended a KIPP school? What was your experience?
Until next time, enjoy whatever you learn.
See the 6 Comments below.
