IntMath Newsletter: Calculators, atomic clocks, tensors
By Murray Bourne, 23 Sep 2019
23 Sep 2019
In this Newsletter:
1. Popular on IntMath: Calculators
2. Resources: Music lab, Webinars
3. Math in the news: AI, atomic clocks
4. Math movies: Tensors, irrationals
5. Math puzzle: Hexagon
6. Final thought: They knew
Today is equinox (equal day and night), where the center of the sun is directly above the equator (very near where I live). In the Southern hemisphere, it's the beginning of spring.
1. Popular on IntMath: calculators
The various calculators on IntMath continue to be popular among visitors.
 |
One of the most popular interactive applets is the Polar to rectangular calculator which not only converts between two ways of expressing complex numbers, but also has an interactive graph that visualizes the concept. |
Some of the other calculators are:
There are now over 200 interactive applets on IntMath. You can see a list of all of them here:
Interactive applets on IntMath
2. Resources
(a) Chrome Music Lab
Most music has elements of rhythm, melody and harmony, which are all mathematical in nature.
 |
Chrome Music Lab contains several interactive experiments that let you explore harmonic series, spectrogram and a melody generator. In the process, you'll see math in action. See: Chrome Music Lab |
(b) Wolfram Language Webinars
Here's another round of free Webinars from the people who bring us Wolfram|Alpha where you'll learn what's new in Mathematica and Wolfram Language 12. Each of these is on a Wednesday, 5-6pm GMT (3pm in Sydney, 10pm Tue in LA).
- 25 Sep: Astronomy and Space Science Entities
- 2 Oct: Mathematical and Statistical Computation
- 9 Oct: Chemistry and Molecular Visualization
- 16 Oct: Microcontroller Deployment and Unity Game Engine Interface
- 23 Oct: Interacting with Blockchains
3. Math in the news
(a) A Breakthrough for A.I. Technology: Passing an 8th-Grade Science Test
Driven by neural networks (mathematical systems that learn by analyzing huge amounts of data), AI has much potential, but also poses dangers.
 |
The Allen Institute for Artificial Intelligence has produced a system that passed an 8th grade science test with a score of 90%, and a 12th-grade exam at 80%. See: A Breakthrough for A.I. Technology: Passing an 8th-Grade Science Test |
Note:
- The test did not include any diagram-based questions; and
- The test was multiple-choice
These are significant limitations in my view. Scientific thinking cannot be adequately assessed via multiple choice.
However, this is still quite an achievement and is yet another step forward in the inevitable advancement of AI.
(b) Why Do We Need Super Accurate Atomic Clocks?
Did you know that not only do we need leap years (the Earth's rotation around the sun is very nearly 365.25 days), we also need leap seconds (there has been around 1 leap second added to UTC (aka GMT) every 2 years since 1972)?
 |
From accurate GPS to the timing needed for coordinating computers across the world, super-accurate atomic clocks are essential. This readable summary gives some good background. |
4. Math Movies
(a) What's a Tensor?
Daniel Fleisch of Wittenberg University specializes in electromagnetics and space physics.
 |
In this video, he gives a good, simple explanation of tensors and their relation to vectors, using simple household objects. See: What's a Tensor? |
His passion for explaining things to others is obvious.
(b) Making sense of irrational numbers
The Pythagoreans had their fundamental beliefs questioned by the philosopher Hippasus, who showed √2 could not possibly be a rational number.
 |
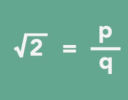Ganesh Pai gives us the background in this TED-Ed video. |
5. Math puzzles
The puzzle in the last IntMath Newsletter asked about a mystery object.
There was only one attempt at an answer (by Nicola, who guessed it was an abacus).
One possible approach to image search: The easiest way to find out what an image could be is to take a picture of it with Google Lens (on your phone). This brings up many sites talking about – and naming – the object.
Another approach: Right clicking on the image (on the blog copy of the Newsletter) and choosing "Copy image address" and pasting that into the search box on Google Images also brings up many results.
The object was a kleroterion, used by the ancient Greeks to randomize the selection of citizens (male, of course) to the boule (local council), to political roles, and as court jurors. (See more: Kleroterion)
It was basically like a modern-day lotto machine, that spits out numbered balls.
New math puzzle: Hexagon probability
Find the probability for a point chosen randomly within the octagon to be blue. The red triangles are equilateral.
You can leave your response here.
6. Final thought - they knew there were concerns, but went ahead anyway
I was watching a documentary about the 1980s recently, and it included the tragic events of the explosion of space shuttle Challenger, which held the first teacher in space, Christa McAuliffe.
The engineers knew there were safety concerns (it was a very cold day and vital O-rings failed, a highly probable outcome known for over a decade previously), but went ahead with the launch.
Later this century, when several tipping points have occured and climate change becomes irreversible, kids will ask their grandparents, "You knew it was a risk, so why did you let it happen?"
Until next time, enjoy whatever you learn.
See the 12 Comments below.
23 Sep 2019 at 11:13 pm [Comment permalink]
Ans. (5+4sqrt3-3sqrt2)/(4+2sqrt3)
Prove octagon is regular(its simple so I'll not explain)
Find side of octagon in terms of length of equilateral triangle by dividing octagon into 8 triangles.
Find probability by calculating area.
Enjoy cup of coffee.
24 Sep 2019 at 4:12 am [Comment permalink]
I am a subscriber to your program, which is very well presented. I presume the calculators too which you make reference in your letter, are accessible via your web site. If this is not the case, please let me know. Also, are there other calculators that you recommend whether as individual calculators ie Texas Instruments and/or online calculators.
Thank you for helping so many with understanding mathematics.
John
24 Sep 2019 at 6:06 am [Comment permalink]
I am sooo glad to see the material on tensors. The thing that first put me in touch with your marvellous newsletter! Well done!
24 Sep 2019 at 11:33 am [Comment permalink]
@Peter: Good to hear from you and thanks for being a loyal reader for over a decade!
24 Sep 2019 at 11:59 am [Comment permalink]
@John: You're welcome!
In each of the 5 examples in the Newsletter, they are online calculators, and that's where the links take you. For quite some time now, the free online offerings (like Wolfram|Alpha and Desmos) have actually been a lot more useful than physical calculators. (Of course, physical calculators make sense in educational settings where not everyone has access to a computer, but there are plenty of phone apps that serve most school-level purposes.) It's been quite a few years since I pulled my Casio from the drawer!
24 Sep 2019 at 9:38 pm [Comment permalink]
I apologize because my English is not good ....The required possibility is to divide the area of blue shapes by the area of the regular octagon and by assuming the length of the square side L AND calculate the area of each shape separately note that the measurement of the angle of the octagon 135 degrees and the measurement of the angle of the regular triangle 60 degrees and therefore be measured angle blue shape 75 / 2
S.A. OF SQUARE = L× L
sS.A. of each triangle = 1/ 2 × L × L sin 60
S.A OF EACH Rhombus = L× L SIN 75 /2
26 Sep 2019 at 2:22 pm [Comment permalink]
The methodology I used was to calculate the area of the octagon and subtract areas for the square and four equilateral triangles; that leaves the four trapeziums shaded blue. Then calculate the ratio of the areas of the Trapeziums to the octagon.
I don't have mathematical formatting and it's a bit tedious written in full but the ratio reduces to,
(1 + sq root 2) a to power 2
-----------------------------
2(1 + sq root 2) a to power 2
= 1/2 or 50%
28 Sep 2019 at 12:05 am [Comment permalink]
Prob is 2SQRT(2)/(1 + SQRT(3) + 2SQRT(2))
28 Sep 2019 at 11:13 pm [Comment permalink]
Area of octagon = 2y^2(1+sqrt(2))
Side length of square = x
Area square = x^2
Area triangles = 2sqrt(3)x^2
Total area not included = x^2(1+2sqrt(3))
Half a blue area has side length x opposite angle of 67.5deg, and side length y opposite angle of 75deg. y=sin75(x/sin67.5)
Total area of blue region as percentage = (((area of octagon)-(area of square and triangles))/area of octagon)*100
Substituting in terms of x: ((2(((sin75)x/sin67.5)^2)(1+sqrt2)-x^2(1+2sqrt(3)))/2(((sin75)x/sin67.5)^2)(1+sqrt2))*100
Cancel out all x^2s and put into calculator =78.85% (4sf)
The probability of randomly picking a somewhere that is blue is 78.85%.
1 Oct 2019 at 10:19 am [Comment permalink]
Let a be the length of each side of the yellow square. All three angles of the red triangles equal pi/3, so that the apothem of each triangle measures h = a cos(pi/6), so that the area of each red triangle is h/2, i.e., a^2 cos[(pi/6)/2.
On the other hand, the distance r from the center of the octagon to the farthest vertex of the red triangles is r = a/2 + h. Consider now any of the eight central triangles which make up the octagon. The apothem from the center to the opposing side measures H = (h + a)/2 cos(pi/8), so that the length of each side of the octagon is b = 2 r sin(pi/8), and hence the area of each central triangle is
b H/2, so that the area of the octagon is 4 b H. The blue areas are then equal to 4 b H - a^2 - 2 a^2 cos(pi/6). On dividing this last expression by 4 b H, all the a^2 cancel out and the required probability is equal to 0.482362 (after some messy arithmetic calculations).
This result can be checked if the radius of the circumscribed circle of the octagon is normalized, and the Area function of Mathematica is used on the resulting graphic.
1 Oct 2019 at 11:32 am [Comment permalink]
"When climate change becomes inevitable."
It is happening now and further changes are inevitable.
Thanks for the other stuff; I value your newsletter.
1 Oct 2019 at 3:10 pm [Comment permalink]
@Bob: Thanks for the kind comment. Of course, I meant "irreversible" and had already amended the post. (A case of thinking about the next thing to type while typing something else...)