IntMath Newsletter: Curvilinear, anchoring, pancakes
By Murray Bourne, 16 Jan 2019
16 Jan 2019
In this Newsletter:
1. New on IntMath: Curvilinear motion animated graphs
2. Estimation and the anchoring principle
3. Bill Gates and his pancakes
4. Math movies
5. Math puzzle: Who dies?
6. Final thought: Truth
1. New on IntMath: Curvilinear motion animated graphs
If the concepts are new to you, it's often hard to determine what's really happening in mathematics problems. I remember struggling with the concepts of x-position in space at time t, y-position at time t and then a particle's position in x-y space at time t. I added some animations to the Curvilinear Motion page to make things a bit clearer.
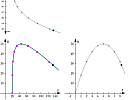 |
You'll see the animations towards the bottom of the page, after the explanation and examples. Go to: |
Of course, in this work, like most mathematics, it's essential to label your axes correctly!
2. Estimation and the anchoring principle
Most of you know I'm a big fan of employing technological approaches to "doing math". It doesn't make a lot of sense to me that we still make students churn through endless algebra exercises, when such things are much more quickly and accurately done by computers.
However, such approaches come with a large danger - a small misunderstanding when setting up the computer to solve a problem can have drastic implications for the solution, which can turn out to be very wrong.
So even more these days, good estimation skills have become essential. Before we ever get a computer (or calculator) to solve a problem for us, we should step back and come up with a "ball park figure" for the final answer. If the computer gives a very different answer to what we expected, we need to investigate further.
With these thoughts in mind, I was interested to come across this article by the Norman Nielsen Group (user-experience experts) on the Anchoring Principle, an important concept for learning, but it can also be used by advertisers and political parties to sway opinions.
 |
The first part of the article discusses some very interesting experiments in estimation. How did you go? Go to: The Anchoring Principle |
(The remainder of the article talks about how to apply the results to better user experience - which is worth reading for anyone who ever uses - or will design - a computer interface!)
3. Bill Gates and his pancakes
In the photo, we see a stack of pancakes where some have a larger radius than others. What if we needed to flip the stack so the largest pancake is on the bottom, and each subsequent one is smaller as you go up? What is the minimum number of flips needed to achieve this?
This was a problem given to a Harvard undergraduate class in the 1970s, and Bill Gates was the first to solve it, with an elegant solution.
See the full story from National Public Radio:
Before Microsoft, Gates Solved A Pancake Problem
Here is the actual paper "William Gates" published in 1979.
Bounds for sorting by prefix reversal [PDF, 11 pages]
Of course, efficient sorting is essential in computer operations, and I suspect that's why he was interested to solve this.
4. Math Movies
(a) How to spot a misleading graph
There are still some of us who regard finding the truth as an important human endeavor.
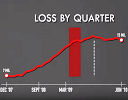 |
Many times, we can be distracted or confused by graphs that deliberately try to mislead. |
(b) How religion spread around the world
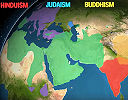 |
This animated map follows a timeline, showing how and when the major religions spread around the world. See: Animated map shows how religion spread around the world |
5. Math puzzles
The puzzle in the last IntMath Newsletter asked about divisibility of a number. Correct answers with sufficient explanation were submitted by Ibrahim, Ajayshukla, Georgios, Alex, Elizabeth, Russell, Saikrishna, Aidan, Bandu, Vijay, Charles, Tugume, Kevin, Tomas, Gerard, and Alfredo.
Special mention to Ibrahim and Bandu who made use of the math entry facility in the blog comments.
New math puzzle: Who dies?

You can leave your response here.
6. Final thought - Truth
Yolande Cornelia "Nikki" Giovanni, Jr. is an American poet, writer, commentator, activist, and educator. Her words are particularly relevant today.
"If now isn't a good time for the truth I don't see when we'll get to it." [Nikki Giovanni]
Until next time, enjoy whatever you learn.
See the 12 Comments below.

16 Jan 2019 at 4:59 pm [Comment permalink]
Nobody dies
16 Jan 2019 at 8:54 pm [Comment permalink]
No one dies.
As the ball have less weight and one side oppen.
And ball will stop over.
Hence no one dies
16 Jan 2019 at 10:22 pm [Comment permalink]
D and e
17 Jan 2019 at 1:10 am [Comment permalink]
No one.
17 Jan 2019 at 5:25 am [Comment permalink]
D will die
18 Jan 2019 at 12:49 am [Comment permalink]
C&B&A will die if E pushes the stone
18 Jan 2019 at 3:07 am [Comment permalink]
No one dies. The cut-out on the boulder saves D, the radius of the teeter totter strikes the wall, plus the lower weight of the initial boulder cannot lift the second boulder, thereby saving C, so therefore the system comes to a halt, allowing all to live a long and prosperous life.
22 Jan 2019 at 12:41 am [Comment permalink]
I would say, that if E pushes the stone C will die.
22 Jan 2019 at 2:13 am [Comment permalink]
The stone may kill any of them
8 Feb 2019 at 6:44 pm [Comment permalink]
c and d.
14 Feb 2019 at 3:02 pm [Comment permalink]
There's quite a divergence of answers! Here's my take.
To get a better idea of what's happening, I overlaid a grid with the same dimensions given in the original image. This is the starting scenario:
The stone rolls 0.5 units before it heads down the slope:
This is the position ater travelling π = 3.14 units:
The slope has length 5 (it's a 3-4-5 triangle) and with another 0.8 of a unit, the total distance rolled by the time the stone reaches D is 2π = 6.28 units, making a mess of person D:
When the stone falls onto the seesaw, C has an unfortunate demise:
A key question is whether the rolling stone has enough momentum to project the other stone (which is heavier) high enough and far enough to land on B. (Notice there's also a small ledge at the left end of the seesaw, which will reduce the distance the stone will go to the left.) It's possible the heavier stone brings the motion to a stop, thus saving C.
I shall leave further speculation up to the reader.
16 Feb 2019 at 1:56 am [Comment permalink]
C and E will be hurt