IntMath Newsletter: Implicit, Observable, Navier-Stokes

28 Mar 2019

In this Newsletter:

1. New on IntMath: Implicit graph plotter
2. Resources: Unofficial Desmos, Observable
3. Math in the news: Navier-Stokes
4. Math movies: Math anxiety, Wind
5. Cattle functions
6. Math puzzle: Repeated digits
7. Final thought: Stats, effort and money

1. New on IntMath: Implicit graph plotter

The majority of the graphs we come across are of explicit functions. These are ones where there is a "y" on the left of the equation, and all the x-terms are on the right. Examples:

y = x²

y = sin(x)

y = 1/x

Such functions have one y-value for each x-value we substitute in. As such, they are relatively easy to graph using computers, because we can choose a set of x-values, substitute them in, and join the resulting (x, y) pairs, similar to the way we sketch graphs on paper.

On the other hand, implicit functions appear with x- and y-terms mixed together, and often it's impossible to separate them such that we are left with a simple "y" on the left. Here are some implicit functions:

sin(x² + y³) = √(x + y + xy)

x² + y² = 25 log(x + y)

These implicit functions are much harder to graph using a computer, since we can have a lot more than one value for y for each value of x, so finding all the correct ordered pairs and then joining them can be quite a programming challenge.

I recently added an implicit graph plotter which uses a technique called Interval Arithmetic, that ensures each pixel in a vertical interval is catered for using variable-width x-intervals, and does quite a good job of addressing the many issues involved in graphing implicit functions.

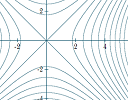Here's some background and examples: Implicit plots in ASVG via Interval Arithmetic, D3 and Function Plot

You can see it in action on this page:

Differentiation of Implicit Functions (see the main page, and then the answers for Example 2 and 3.)

2. Resources -

(a) Unofficial Desmos

Desmos Graph Calculator is a great tool for exploring mathematics, and for setting up interactive applets for others to use.

Sometimes the documentation for Desmos is not as extensive as you may like.

DesmosGraph – unofficial aims to fill that gap by providing tips and tricks for how to get the most out of Desmos.

(b) Observable

Observable is a "magic notebook for visualization, exploring data, interactive essays and live coding".

The concept is similar to Wolfram's Notebooks (and SageMath), but Observable is free and open source (as is Sage).

Observable is a neat Web-based math coding solution that can produce a wide variety of data visualizations. Go to: Observable

See visualization examples.

Don't miss this demo and these Tutorials.

Observable has a lot of potential for class projects, and for writing up science lab results.

Observable is by Mike Bostock, American computer scientist and data-visualisation specialist and one of the creators of D3.js, a brilliant javascript data visualization library.

3. Math in the news: Navier-Stokes equations under review

The Navier-Stokes equations describe what's going on when fluids move and interact. They are extensively used to model the weather, ocean currents, air moving over aircraft wings and even for simulating effects in computer games.

The equations have been in use since their development in the 19th century, generally with great success. However, there's a problem.

Do they work?

Most observations confirm the Navier–Stokes equations do "work", but mathematically, there are still several doubts about them, precisely because they follow from observation, rather than being the result of mathematical rigor. It's not even known whether the solutions always exist in 3 dimensions, nor whether they are continuous.

There's a $1 million reward for anyone who can mathematically prove they work, or provide an example where they don't.

For an interesting discussion on the issue from Quanta Magazine, see: Mathematicians Find Wrinkle in Famed Fluid Equations

4. Math Movies

(a) Why do people get so anxious about math?

Some studies have shown up to 20% of people suffer from math anxiety. We're not talking about the usual butterflies we all get when facing a test.

Math anxiety is a serious, debilitating condition that has enormous implications for people. See: Why do people get so anxious about math?

(b) The Boy Who Harnessed the Wind: William Kamkwamba

Willaim Kamkwamba grew up in the grinding poverty, drought and hunger of Malawi, in southeast Africa.

Thrown out of school because his father couldn't pay the fees, 13 year-old William sets about inventing a wind turbine to power electrical devices, including a water pump.

Through his own grit, inventiveness and willingness to find things out by himself, he has built other wind turbines and a solar power unit.

In 2014 he received a Bachelor of Arts degree in Environmental Studies from Dartmouth College, USA.

Here's his TED talk: How I harnessed the wind

The BBC recently made an inspiring movie about the story, now showing on Netflix. Here's the trailer: The Boy Who Harnessed the Wind.

5. Cattle functions

I hope these trigger memories next time you need to sketch (or make use of) a polynomial or cosine function. 🙂

[Image source]

6. Math puzzles

The puzzle in the last IntMath Newsletter asked about integers with remainders when divided by certain numbers. Correct answers with sufficient reasons were submitted by Chris, Rick, Russell, Thomas, Vijay and Ben.

Historical note: This remainder problem was first stated in the 3rd century Chinese mathematical treatise Sun Zi Suanjing.

A generalization of the problem is known as the Chinese Remainder Theorem. A special case of the theorem asks for the smallest integer giving 1 as a remainder when divided by each of 4, 5 and 6. The LCM of 4, 5 and 6 is 60, so the required number is 61. (All numbers meeting this condition are in the form 60n + 1).

The Chinese Remainder Theorem came to the West via the 11th century Arab scholar Ibn Tahir and then by Leonardo Fibonacci in his early 13th century treatise Liber Abaci.

New math puzzle: repeated digits

A 4-digit number pqrs (where p ≠ 0 and the digits are not necessarily unique) is multiplied by 1999, resulting in a number which ends with 4 repeated digits. Find all possible numbers pqrs.

You can leave your response here.

7. Final thought - statistics, effort and money

The news is full of statistics. Usually it's a simple count of the number who died in an accident, or who were affected by some natural disaster.

I'm always impressed how air crash investigators rush to the scene of an aircraft accident, and how huge resources are invested in the investigation and follow up actions. The aircraft industry is important to all countries, and it's in everyones' interest to ensure safe operation of aircraft. I get that.

However, what of the other deaths - the ones we don't hear about every day on the news. How about:

• Worldwide, tobacco kills more than 7 million people each year. More than 6 million of those deaths are the result of direct tobacco use while around 890 000 are the result of non-smokers being exposed to second-hand smoke. [Source: WHO]
• Worldwide, 3 million deaths every year result from harmful use of alcohol [Source: WHO]

The efforts put into reducing these 10 million deaths (around 10,000 times the number who perish in air accidents annually) is nothing like the relative effort put into solving (for example) the Boeing 737 Max8 issue. Sadly, as is the case for many things, it comes down to the profit involved.

In Bill Gates’ commencement speech at Harvard when he was awarded an honorary degree in 2007, he's talking about the same thing:

When an airplane crashes, officials immediately call a press conference. They promise to investigate, determine the cause, and prevent similar crashes in the future.

But if the officials were brutally honest, they would say: “Of all the people in the world who died today from preventable causes, one half of one percent of them were on this plane. We’re determined to do everything possible to solve the problem that took the lives of the one half of one percent.”

The bigger problem is not the plane crash, but the millions of preventable deaths.

Until next time, enjoy whatever you learn.

See the 10 Comments below.