IntMath Newsletter: Resources, primes, matrix app and role models

2 Oct 2013

In this Newsletter:

1. Resources for the new school year
2. Prime Gaps
3. Math interactive: matrix applet
4. Math puzzles
5. Friday math movies
6. Final thought - Choosing the best role model

September was a very busy month. My hours as a freelance trainer continue to climb, leaving me with less time to devote to writing.

Welcome to all the new subscribers to the IntMath Newsletter (there's now over 13,000 of you). I'll try to be more regular!

1. Resources for the new school year

These articles have proved popular over the years. I hope you find them useful, too.

• Ten Ways to Survive the Math Blues
• How to understand math formulas
• How to learn math formulas

Here are some explanations of math topics that often cause grief:

• What is trigonometry all about?
• Logarithms – a visual introduction

And here are some articles that have generated quite a bit of interest:

• How to find the equation of a quadratic function from its graph
• Is 0 a Natural Number?
• Top 10 math help sites

And for the math teachers among you, this might give you some ideas when preparing your lessons:

• How to make math class interesting?

2. Prime Gaps

Prime numbers have fascinated mathematicians for centuries. More recently, they have become increasingly important for their use in encryption. The search for ever-larger primes is crucial for ensuring safety of online financial (and other) transactions.

An interesting question is: how "dense" are the primes?

Clearly they are less dense as the numbers get bigger.

For example, in the first 5 positive integers, we have 3 primes (2, 3 and 5) so the "density" is 3/5 = 60%. The average "gap" between these primes is 5/3 = 1.3333...

In the first 10 positive integers, we have 4 primes (2, 3, 5, and 7), so 40% of the numbers are primes and the average gap is 10/4 = 2.5, which of course is almost twice the gap of the first 5 integers.

Let's now consider the primes less than 30. There are 10 of them (giving a density of 33.3%), and the average gap is 30/10 = 3.

There are 25 primes less than 100, (25%), and the average gap is 100/25 = 4. Our gap gets bigger the further out we go.

For the integers less than 1000, we have 168 primes, and the gap is 1000/168 = 5.95.

If we go all the way out to one billion, only 5.1% of the numbers are prime (in fact there are 50,847,534 of them), and the average gap has grown to around 19.667.

Is there a formula for estimating the gap between the primes?

An estimate for the prime gap

Brilliant German mathematician Carl Friederick Gauss noticed:

The gap between primes as N becomes large is approximately log_eN.

He was just 15 years old at the time he wrote this!

For the case of one billion, log_e 1000000000 = 20.723, which is quite close to the actual gap of 19.667.

[This section on Prime Gaps is based on a chapter in Joy of x, by Steven Strogatz. I recommend this book!]

Here's a graph of the gap size against the prime number size. We can see the distribution of the gaps is basically logarithmic.

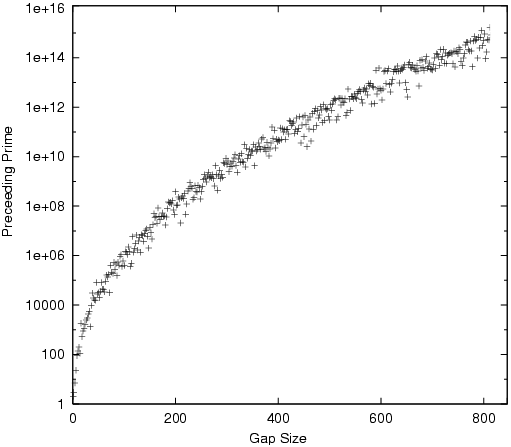
[Image source: First Occurrences of Prime Gaps, by Herzog, S.]

3. Math interactive: matrix applet

Here's an applet where you can investigate how matrix operations work. It's an update so that it can work on mobile devices. Updated matrix interactive

4. Math puzzles

The puzzle in the last IntMath Newsletter asked about the probability of a woman having breast cancer, given that she has a positive mammogram.

Answers with explanation were given by Mawanda, Francis and Nicos. Each answer correctly involved finding the ratio of those who test positive and have cancer, to those who test positive but don't actually have cancer. The calculations differ slightly, but they ended up with answers around 10%. Nicos' answer was correct, at 9.44%.

The background to this was a study by Gerd Gigerenzer who asked doctors in Germany and the United States to estimate the probability. The answers he got ranged all the way from 1% to 90%. This is a bit scary when we consider such calculations can lead to decisions that could be life-threatening.

The story is recounted in Strogatz's Joy of x. You can read more about this puzzle in his New York Times article, Chances Are (you now need a subscription to get in).

New math puzzle

Show that the sum of the infinite series 1/10 + 2/100 + 3/1000 + ... when written in decimal form does not contain the digit 8.

Leave your responses here.

5. Friday math movies

(a) Imaginary Numbers Imaginary numbers are the result of some mathematical creativity, but have many applications in science and engineering. Friday math movie: Imaginary Number

(b) A clever way to estimate enormous numbers This video shows how to use powers of 10 to make estimates of large numbers. Friday math movie: A clever way to estimate enormous numbers

6. Final thought: Choosing the best role model

All of us copy those we admire, whether we are conscious of it or not. Sometimes we carefully choose a role model, but often we just glean our attitudes and approaches to learning from those around us - good or bad.

Annie Murphy Paul has some great advice in "How to Choose a Role Model Who Will Really Motivate You". Research shows that we shouldn't try to emulate the very top people in our profession, because that can too often lead to disappointment and demotivation. Rather, choose those in the second tier. We can better learn from such people the way they cope with failure and setbacks.

There's also some interesting research in that article about how best to motivate girls to undertake STEM (science, technology, engineering and math) courses.

Until next time, enjoy whatever you learn.

See the 3 Comments below.