IntMath Newsletter: Phi, music and maps
By Murray Bourne, 05 Sep 2013
5 Sep 2013
In this Newsletter:
1. Resource: Dr. Geo
2. Music and Phi
3. Maps that help you make sense of the world
4. IntMath Poll
5. Math puzzles
6. Friday math movies
7. Final thought: Clear vision
1. Resource: Dr. Geo
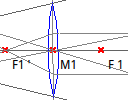 |
Dr Geo is a free download that allows us to construct a wide variety of geometric objects. |
2. Music and Phi

Phi (Φ) is known as the "Golden Ratio" and has value 1.618 033 988... It is the positive solution to the equation Φ2 − Φ − 1 = 0 and has some quite remarkable properties.
Phi and its reciprocal, 1/Φ = 0.618 033 988... have been observed to occur in nature. The Φ ratio has a connection to the Fibonacci numbers (the ratio of successive Fibonacci numbers approach the value Φ.)
Many people believe that beauty is related to this Golden Ratio. If someone has body proportions (and facial proportions) which follow the Golden Ratio, we tend to find such people "attractive". (See Math of Beauty.)
I came across the following article recently, where it talks about how the Golden Ratio is used in computer game music, to make it more pleasing to the ear, and to provide contrast via climaxes:
Zelda Music of Golden Proportions
And here's a short music video based on Phi by Michael Blake:
What Phi (the golden ratio) sounds like.
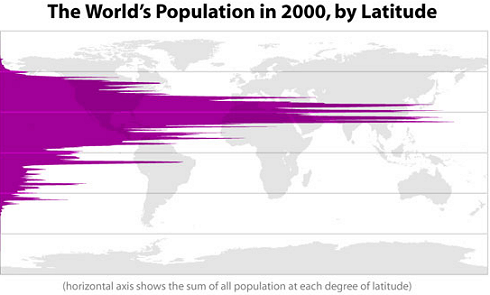
3. Maps that help you make sense of the world
Here's a nice resource. I love maps and I love visual statistics, and this interesting collection has both.
In Maps that will help you make sense of the world, by "Twisted Sifter", we learn about global distribution of all sorts of things, including researchers, vegetation, McDonalds, alcohol consumption, writing types and many more.
Here's one of the maps, showing the distribution of people by latitude.
This is how math relates to the real world - it helps us to describe the human condition.
4. IntMath Poll
The recent IntMath poll asked readers how they feel about summer holidays.
The most interesting thing about this result is the 17% who regard summer holidays as "too long".
I feel summer holidays are:
Not long enough: 63%
About the right length: 20%
Too long: 17%
Total votes: 1800
Current IntMath poll: Now that summer holidays are over for most of you, the latest poll asks how you feel about school. You can answer on any (inner) page of IntMath.com.
5. Math puzzles
The puzzle in the last IntMath Newsletter asked about the distance travelled by a car in a fuel efficiency test.
Correct answers with explanation were given by Francis Kisner and Sai Krishna.
New math puzzle
Estimate the probability that a woman who has a positive mammogram actually has breast cancer, even though she's in a low-risk group: 40 to 50 years old, with no symptoms or family history of breast cancer. Assume the following statistics:
- The probability that one of these women has breast
cancer is 0.8 percent. - If a woman has breast cancer, the
probability is 90 percent that she will have a positive
mammogram. - If a woman does not have breast cancer, the probability is 7 percent that she will still have
a positive mammogram.
Please leave your responses here.
6. Friday math movies
These 2 math movies show how art and math can be intertwined.
 |
(a) The beautiful math of coral (and crochet) How do we get the message out about saving corals from destruction? Here's one way involving community crochet. Friday math movie: The beautiful math of coral (and crochet) |
 |
(b) Fractals and African designs This is an interesting story about how Africans used fractal ideas for their designs. |
7. Final thought: Clear vision
Richard Nelson Bolles was talking about job-seeking when he wrote in the book What Color is Your Parachute?:
The clearer your vision of what you seek, the closer you are to finding it. For what you are seeking is also seeking you.
I see it all the time when students have a clear vision about what they are doing and where they are going. Such students tend to be more successful in their studies.
Until next time, enjoy whatever you learn.
See the 6 Comments below.
8 Sep 2013 at 11:31 pm [Comment permalink]
p(breast cancer / mammogram)= p(breast cancer n mammogram)
p(mammogram)
= (0.8 x 0.9)/(0.8 x 0.9+ 0.2x0.07)
= 0.72/(0.72 +0.014)
= 0.72/0.734)
= 0.9809264305
= 0.981.
10 Sep 2013 at 8:41 am [Comment permalink]
The music of mathematics needs to be revamped. If you use base 10 numbers and slap them into major or minor scales, they end up sounding random.
Listen to the beauty in pi base 12 assigned to the chromatic scale. All I did was add chords and time the melody notes. It is as unobstructed as is possible.
https://www.youtube.com/watch?v=GrsV5dHXeV0&feature=youtu.be
10 Sep 2013 at 8:47 pm [Comment permalink]
@Jimmy: Thanks for sharing. You may be interested in this article: A logarithmic music scale.
But your base-12 scale makes a lot of sense.
17 Sep 2013 at 8:41 am [Comment permalink]
We are given that 0.8% of women in the group have the cancer and that of those who do, 90% have positive tests. That is 0.008(0.90) = 0.0072 test positive and have cancer.
Also, since 0.8% have cancer, 99.2% do not. Of those who do not, 7% test positive.
That is 0.982(0.07)= 0.6944 test positive but do not have cancer.
The ratio of these results 0.0072 / 0.6944 = 10.37% which seems to me to be the probability that a woman in the group tests positive and has the cancer. This rather low likelihood is the result of the fact that the test has a relatively high false positive rate among an overhelmingly large part of the population who are not ill. The combination results in many, many more false positives than there are true positives.
Alas, this situation is not uncommon in testing.
18 Sep 2013 at 10:55 pm [Comment permalink]
Suppose 100000 women between 40-50 years old. 800 of them have breast cancer. Then 0.9*800=720 have mammog. positive.
100000-800=99200 women have not cancer. Then 0.07*99200=6944 of them are mammog. positive. The total number of mammog.+ women is: 6944+720=7664.
So the probability of mammog.+ plus having breast cancer is 720/7664, about 9.44%.
27 Oct 2013 at 10:39 am [Comment permalink]
Dear sir,
I am using Baye’s theorem for this problem. answer I got is 9.39 percent.
explanation:
let Event1(E1) : having breast cancer
Event2(E2) : not having breast cancer
Event A : having positive mammogram.
it is obvious that these E1 and E2 are mutually exclusive and
exhaustive. So we can use the Baye’s theorem.
if follows that P(E1) = 0.008 (as given)
P(E2) = 1 – P(E1) = 0.992
P(A|E1) = 0.90 (as given)
P(A|E2) = 0.07 (as given)
P(A intersection E1) = P(E1) * P(A|E1) = 0.0072
P(A intersection E2) = P(E2) * P(A|E2) = 0.06944
then from Baye’s theorem
P(E1|A) = probability of having cancer if she has positive
mammogram = (P(A intersection E1))/(P(A intersection E1)+P(A
intersection E2)) = 0.0072/0.07664 = 0.0939
hence answer is 9.39 percent.
Notation used:
P(x) : probability of x
P(X|Y) : probability of happening of event X if event Y is happened.
conditional probability.