Logarithms - a visual introduction

One of my regular correspondents, Yousuf, recently became very confused over what "log" meant. He'd missed a small, but vital piece of information − that if the base is omitted, it's assumed we are talking about log base 10.

So "log" (as written in math text books and on calculators) means "log₁₀" and spoken as "log to the base 10". These are known as the common logarithms.

We use "ln" in math text books and on calculators to mean "log_e", which we say as "log to the base e". These are known as the natural logarithms.

Many of my students would incorrectly write the second one as "In" (as in In spring, the flowers bloom.)

But how could you blame them? In the font used on most calculators (see photo above), and in many books, it looks more like an "I" (I am hungry) than an "l" (There is a lamb).

And when we need to find the natual logarithm of the number 1, it looks like this:

ln 1

If the spacing is bad, it looks like this:

ln1

Depending on the font used, this could even be confused with this

|n| (the absolute value of n)

Wouldn't it be better for all if it was the following?

log_e1

I feel "log" and "ln" is terrible notation and it is not surprising students get confused. The concept of logarithms is already somewhat foreign, so why make it even more difficult with bad notation?

Where did logarithms come from?

In the early 17th century, due to colonization by the Europeans, world trade was really taking off. There was intense interest in astronomy, since this increased the chances of a ship coming back with its bounty. Clockmakers were also in great demand. All of this required more and more sophisticated calculation.

Activities like banking and trade resulted in huge volumes of calculation, and accuracy was essential. For example, compound interest and the distances of moons, planets and stars involved a large number of multiplications and divisions. But this was very tedious and time-consuming, as well as being prone to error.

Surely there had to be a better way?

Logarithms were developed in the early 17th century by the Scotsman John Napier and the Englishman Henry Briggs (who later suggested base 10 rather than Napier's strange choice). Their ideas were refined later by Newton, Euler, John Wallis and Johann Bernoulli towards the end of the 17th century.

Napier gave us the word "logarithm", from the Greek λoγoς (logos) meaning ratio, and αριθμoς (arithmos, meaning "number"). In Napier's new system, the difference of two logarithms determines the ratio of the numbers they represent, so that an arithmetic series of logarithms corresponds to a geometric series of numbers.

Example

To understand what the above means, let's look at a multiplication example. We are going to multiply the following (without using calculator):

69.18 × 776.25

We could start multiplying (and this would involve 20 multiplications, including carries, in 4 rows plus one row of addition, involving 8 additions plus carries), but imagine what would be involved if there were 7 or 8 digits in each number!

Solution Involving Logarithms

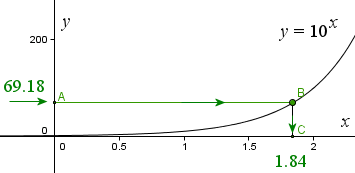
We draw the curve y = 10^x.

We locate 69.18 on the y-axis (point A) and move horizontally until we hit the curve y = 10^x. Then we go vertically down until we hit the x-axis. The value of x we find is 1.84. (They actually would have found this value using a set of tables.)

We do the same thing with the other number. Start at 776.25 on the y-axis, intersect the curve at E, then project down to the x-axis, landing at 2.89.

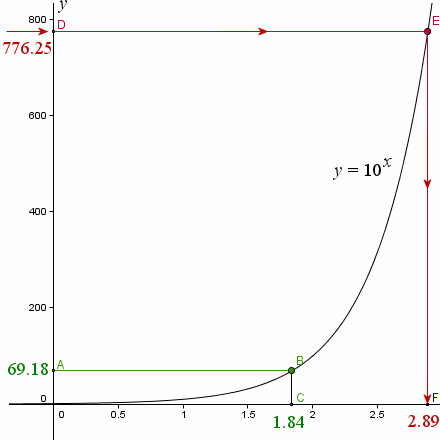
Now, to calculate our multiplication problem, we add the two x-values we found:

1.84 + 2.89 = 4.73

Next, to find the final answer, we do the reverse process. We project 4.73 (point G, at bottom right) up to the curve (point H), then across to the y-axis (point J, which they'd also find using tables).

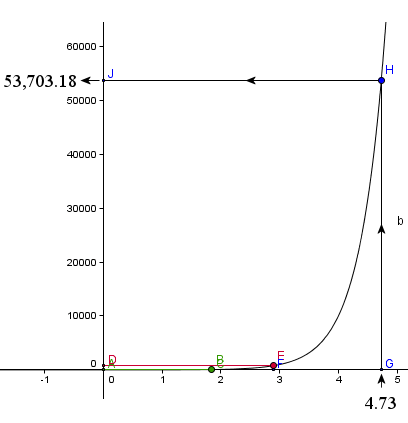
We see we have landed at 53,703.18, which is our solution.

What we have done is to multiply 69.18 by 776.25 and obtained 53,703.18, with out doing any multiplication at all - just adding.

In effect, what we were doing with the graphs was actually using logarithms and we have done the following:

10^1.84 × 10^2.89 = 10^1.84+2.89 = 10^4.73

All logarithm notation does is to let us write the above statement without indices (powers). The equivalent statement using logarithms is:

log₁₀69.18 + log₁₀776.25

= 1.84 + 2.89

= 4.73

In the last step of the graph process above, we found the "antilogarithm" of 4.73. In effect, an antilogarithm of a number is 10 raised to the power of that number. That is,

antilog(4.73) = 10^4.73 = 53703.18

The various log laws are based on the fact when we multiply 2 numbers with the same base, we just add indices (like we did in the example above). See more here: Log Laws.

Logarithm notation is also a function notation, which is more convenient for calculation than if we use powers of 10.

Division Using Logarithms

To perform difficult divisions, you would just subtract the logarithms, rather than add them. The rest of the process was the same. You could find square roots by finding 1/2 of the logarithm.

Note: The accuracy of log tables was an issue for developers. The actual answer for 69.18 × 776.25 using calculator is 53700.975. So working to 2 decimal places throughout has given us an error of around 0.004 of 1% - not much, but still significant when you are talking about distances to other stars. Since our original numbers (69.18 and 776.25) had 4 and 5 significant digits respectively, our final answer can only be accurate to 4 significant figures (the lesser of 4 and 5). So our answer using logs should be written 53700 (the first zero is significant) and this tallies with the calculator answer correct to 4 significant figures. (See Operations with Approximate Numbers on this page Approximate Numbers for more detail.)

Log Tables

For 250 years, logarithms were the primary method for reducing complicated calculations into easier ones. A huge amount of effort was put into creating logarithm tables with as many decimal places as possible for best accuracy. These allowed people to find the logarithm of any number, and after performing the easier calculation, to do the opposite process, and find the antilogarithm.

Logarithm tables were used in schools around the world until the 1980s, when calculators took over.

The slide rule is a device that also relied on ratios of numbers to simplify tedious calculations.

Logarithms to Base e

In most scientific and computing applications, logarithms to base e are used. (e = 2.718281828459..., an important and common mathematical constant.)

It is so common in fact, that "log" is assumed to mean "log base e" in many scientific situations (the opposite of what it means on your calculator).

In many computing languages, it is also assumed "log" means natural logarithm "log base e"), and this only adds to the confusion for engineering students.

Why Do We Still Learn Logarithms?

Even though we don't use logs any more for multiplication and division, the logarithm function (and its related exponential function) are still very commonly used in science and engineering. Logarithms are also important in financial and population studies.

You an see more on logarithms here: Exponential and Logarithmic Functions

Let's Fix Logarithm Notation

Many students, like Yousuf, get unnecessarily confused about logarithms because of the poor notation used.

Natural logarithms: I say we should drop "ln" notation altogether and use "log_e" only, in both text books and on calculators.

Common logarithms: We should only use "log₁₀" notation for common logarithms on calculators and text books.

Even in computer programming we could use "loge" (no subscript needed) for natural log, and maybe "logc" for common logarithms.

Do you agree with my suggestion?

See the 24 Comments below.