Vector fields - a simple and painless introduction
By Murray Bourne, 14 Sep 2009
Vector fields provide an interesting way to look at the world.
First, a quick bit of background. A vector is a quantity with magnitude and direction. A simple example is the velocity of a car that is traveling at 100 km/h in a Northerly direction. The vector representing this motion has magnitude 100 km/h and direction North. We usually represent a vector using an arrow. The size and direction of the arrow indicates the magnitude and direction of the vector. (See more in the Vectors chapter in IntMath.)
Before I tell you what a vector field is, let's look at a few examples. Each of them involves patterns - the building block of all math.
Weather charts - wind speed and direction
The daily weather chart (showing wind speeds) is an example of a vector field. The wind direction and strength is given for different points on the Earth's surface.
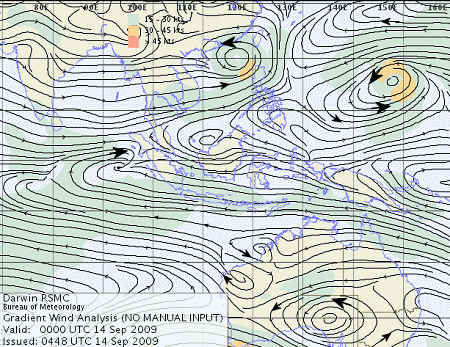
[Image source]
In the above chart of the Australia/South Asia region, gentle winds (across most of the Indian Ocean) are indicated by a small arrow head, and stronger winds by larger arrow heads. Winds rotate around high and low pressure systems, in opposite directions for the Northern and Southern hemispheres.
Below is another wind chart giving us a better idea what a vector field is. This time we are looking at the winds surrounding Cyclone Ike, which devastated Texas in September 2008. The winds in the center were over 200 km/h. (The scale on the chart is in knots, the unit we usually use for wind speed.) The direction of the "F" symbols indicate wind speed, while the color indicates magnitude.
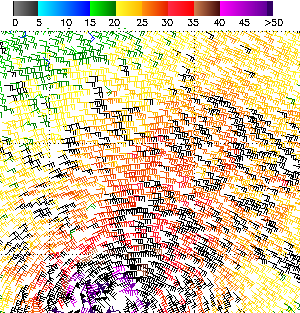
Wind chart - Cyclone Ike from the Quikscat satellite [source]
Another example of a vector field is the pattern made by iron filings when under the influence of a magnetic field.
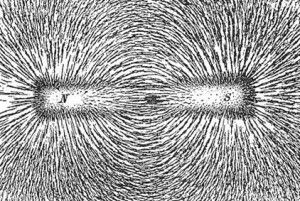
Iron filings lining up around a magnet. Image source
We're ready for a loose definition of a vector field.
Definition of Vector Field
A vector field is simply a diagram that shows the magnitude and direction of vectors (forces, velocities, etc) in different parts of space.
Vector fields exhibit certain common shapes, which include a "source" (where the vectors emanate out of one point), a "sink" (where the vectors disappear into a hole, something like a black hole effect), a "saddle point" (which looks like a horse's saddle), and a "rotation" (where objects rotate around some point, something like a planetary system).
Following are some excellent visualizations of vector fields for you. If you visit the links, you can play with the vector fields to explore the concepts involved.
There's some pretty neat art going on, too, but that's just a lucky outcome.
Rotations, sinks, sources, and saddle points
Visit the following example from the Demonstrations site by Wolfram. These interactives are made using Mathematica. There are 2 things you can do:
- Watch an animation that shows the outcome of parameter changes (click the "watch Web preview" link at the top right of each animation), or
- You can download the Mathematica Player and interact with the documents, and explore by changing parameters. This is recommended!
The link to the interactive: Vector Fields: Streamline through a Point
In this interactive, you can grab the point indicated by the larger dot and explore the direction of the vector field. The developer says:
Drag the locator; the red streamline then passes through that point, illustrating the flow of the vector field. The vector fields show rotations, sinks, sources, and saddle points.
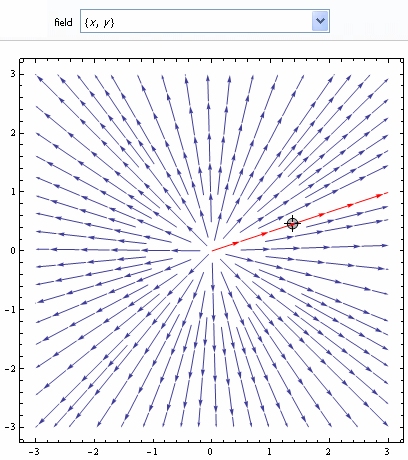
A "source"
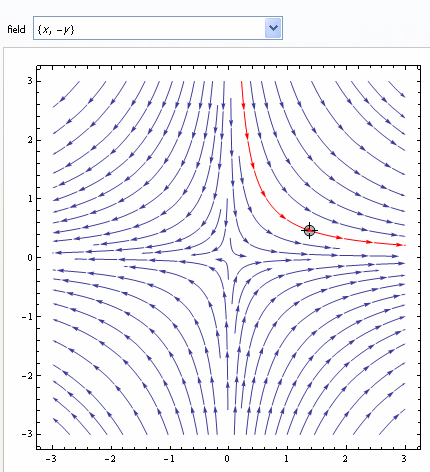
A saddle point
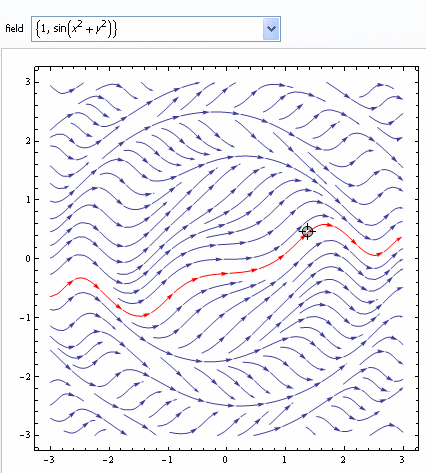
A hilly bowl-shaped vector field
A Neural Network and vector fields
Your brain consists of millions of neural networks. When you start thinking about something, some of your neurons fire and this triggers nearby brain cells to fire. Soon (within milliseconds), a larger network of neurons begins to fire (you are getting excited about what you are thinking about and it begins to consume more of your attention).
This scenario is demonstrated in the following screen shots from the animation: Cellular-Automaton-Like Neural Network in a Toroidal Vector Field
The first torus shows the beginnings of our thought, the second one shows the network after some excitation.

Neurons firing in a neural network
The developer of this interactive says:
Red indicates cellular activity (a neuronal spike) while blue indicates inactivity. Color intensity encodes the value of a binary internal state variable. The weights between each cell and each of its neighbors have been adjusted to reflect Boltzmann-like transition probabilities appropriate for flow in a constant vector field on a torus (the angle of the field is an adjustable parameter in this Demonstration).
Vector Field Java Applet (from Falstad)
This is a superb interactive. There are a huge number of examples here (use the pull-down arrows at the top right of the java applet), with clear animations indicating direction and magnitude (usually velocity or forces involved).
The link: Vector field animations (java applet).
A screen shot:
3-D Vector Fields
Here is an animation from Australia's Bureau of Meteorology showing the wind velocities involved when a high and a low pressure centre interact.
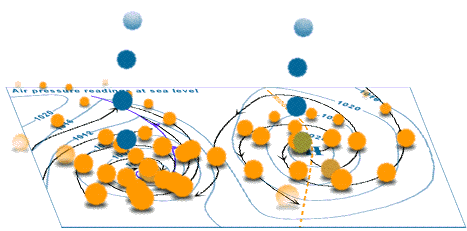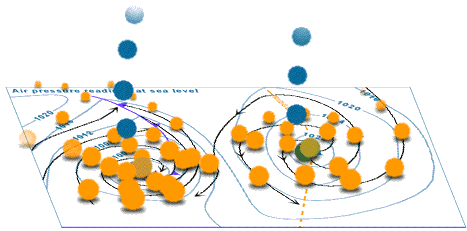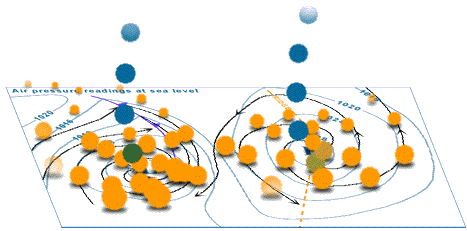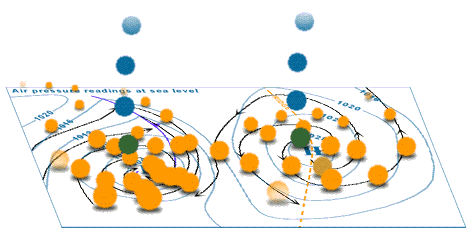
Source: Animations of wind in 3 dimensions
Here are some more examples of 3-D vector fields, once again from Wolfram's Demonstrations.
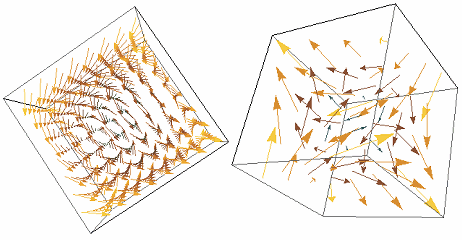
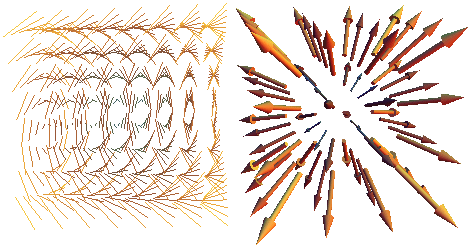
Modeling Game Behaviour
This next one is a vector field related to gaming and learning.
We all learn from experience. We tend to be attracted to strategies (in real life and in games) that were successful in the past. 'Experience-weighted attraction' (EWA) learning is a model of game behaviour where we modify our strategies based on our success with those strategies. For example, in the game of chess, we may find that we are most successful when attacking with our knights, so we continue to use that approach. But our opponent learns what we are doing and develops a good counter-attack. We change our approach.
The mathematics behind all this is that we can estimate probabilities of players changing approach. Since these are multi-dimensional problems, we can draw vector fields representing the probable outcomes.
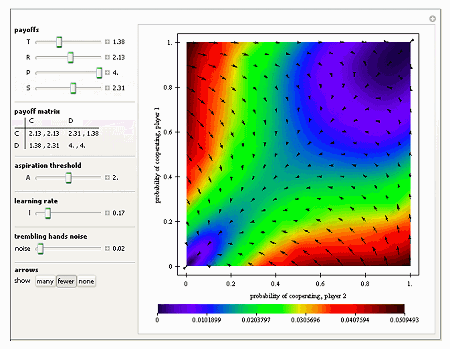
This interactive shows such a vector field. In this game, a player can either cooperate with the other player, one cooperates, the other doesn't, they both defect or the other player defects.
The following variables are involved when two players use the Bush–Mosteller reinforcement learning algorithm playing a symmetric game:
- The payoff a defector gets when the other player cooperates (for temptation);
- The payoff obtained by both players when they both cooperate;(for reward);
- Both players obtain a payoff when they both defect (for punishment); and finally,
- The payoff a cooperator gets when the other player defects (for suckers).
Expected Motion in 2x2 Symmetric Games Played by Reinforcement Learners
Here's what you'll see:
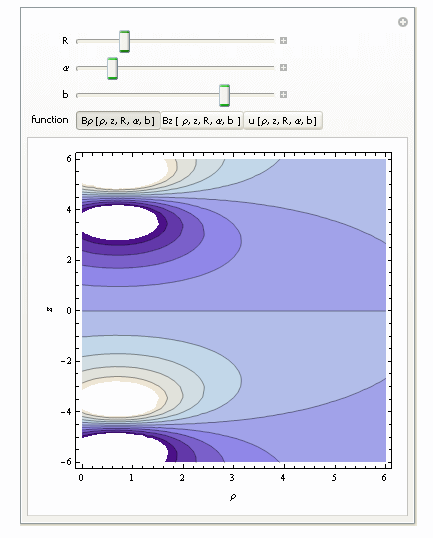
Helmholtz-Coil Fields (Electricity)
Two parallel circular conductors both carry current in the same direction. The circles lie parallel to the x-y plane.
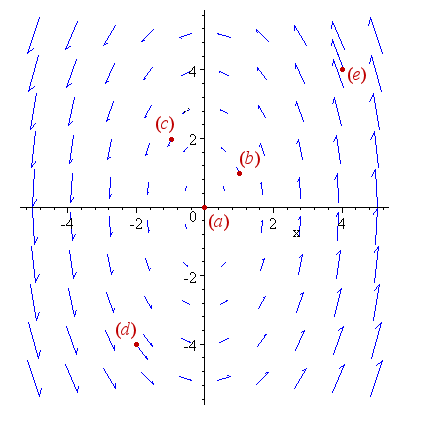
A simple example of a Vector Field
Here's a more formal definition of a vector field. It applies to 3-dimensional space as well.
Definition: A vector field in two dimensional space is a function that assigns to each point (x,y) a two dimensional vector given by F(x,y).
This means every point on the plane has a vector associated with it (with magnitude and direction).
Example: The force operating at a point (x,y) on a surface is given by f(x,y) = (-y,3x)
We could also write this as f(x,y) = -yi + 3xj, where i is the unit vector in the x-direction and j is the unit vector in the y-direction.
Let's see what this means with 4 points in the plane.
(a) If we are at the origin, (0,0), there is no force at all, since f(0,0) = 0i + 0j
(b) At the point (1,1), the force will be f(1,1) = -1i + 3j, so the force is in the up-left direction, with magnitude √10.
(c) Another point (-1,2) will have force -2i − 3j, which points down-left with magnitude √13.
(d) At the point (-2,-4), the force vector will be f(-2,-4) = 4i − 6j that is, a force of magnitude √52 pointing right and down.
(e) Point (4,4) will have force -4i + 12j, which points up-left with magnitude √160 = 12.65.
Here are the 5 vectors we just described. Notice the forces in the middle of the vector field are very small, and they get bigger as you get further from the origin.
That brings us to the end of our exploration of vector fields. They are not scary, despite the way many textbooks present the topic.
See the 16 Comments below.
16 Sep 2009 at 11:58 am [Comment permalink]
Thanks for this. I've never heard of vector fields before, but this gives me some idea what they are all about.
I went looking for other definitions, and you're right - they were hard to understand!
16 Sep 2009 at 6:23 pm [Comment permalink]
WRT your "Simple Example of a Vector Field", is the representation of Point (e) correct? At the point (4,4) the force should be -4i+12j. Am I missing something here?
16 Sep 2009 at 8:02 pm [Comment permalink]
Hi Terry.
I changed the diagram around before publishing and obviously missed that particular alteration. Thanks for pointing it out - I have amended the post.
17 Sep 2009 at 5:20 am [Comment permalink]
perfect...i took the field vector in magnetism...the magnetic field...it was some how unclear for me ..but now it is clear..10x
17 Sep 2009 at 12:10 pm [Comment permalink]
Very good start. Please make it more rigorous by introducing the concept of gadient, divergence and curl. Thus, please explain connotations of Maxwell equations vectorially.
Sirsindhi
17 Sep 2009 at 1:02 pm [Comment permalink]
Hi Aurangzeb
Thanks for the feedback. The intent of this introduction is for people who have never heard of vector fields before, and whose background in math is not as advanced as divergence, curl and Maxwell Equations.
17 Sep 2009 at 2:22 pm [Comment permalink]
Great to see this topic so well put. Please do more like tensors etc (I like pain in the head) Certainly this should be followed up on, curl div and so on could be treated.
21 Sep 2009 at 2:59 pm [Comment permalink]
nice topic can you sent me more on astronomy
25 Sep 2009 at 6:41 am [Comment permalink]
Not an easy topic for me to understand, but appreciate your introducing it. Thanks.
25 Sep 2009 at 3:22 pm [Comment permalink]
One word EXCELLENT.
Looking forward to next newsletter.
max.
29 Sep 2009 at 7:40 pm [Comment permalink]
This is great i am really enjoying teaching maths and my learners are very happy from the time i started receiving e-mails from you.
2 Dec 2009 at 2:39 pm [Comment permalink]
hay... thanks for this e-mail. i don't need to search about vectors anymore for you already gave me about this topic.. thanks.
4 Dec 2009 at 2:21 pm [Comment permalink]
This is great. it makes it easy for me as a lecturer of mathematics to explain to my student teachers who will in turn explain the concepts well to their pupils. I would also appreciate if you could send me some similar ideas on complex variables and any other areas of mathematics.
3 Dec 2011 at 2:37 pm [Comment permalink]
thanks MURRAY.......! FOr giving us such a nice and useful information.it help me alot.....
26 Mar 2017 at 4:52 pm [Comment permalink]
A big (but admittedly late)thank you from a far away land,for the nice, clean and simple introduction(and a bit more than an introduction i guess)..:)
Nice one Murray.Thanks man!
11 Jul 2018 at 6:22 pm [Comment permalink]
Vector field is an awesome concept. I never heard before, but while I read your article, I can know some valuable things related to vector images. However, thank you so much for sharing this type of unique idea.