IntMath Newsletter: Latest applets, visual math
By Murray Bourne, 31 Jul 2014
31 Jul 2014
In this Newsletter:
1. Latest interactive math applets
2. Resource - Context Free math-based art
3. Color Blindness graph simulator
4. IntMath Poll results
5. Math puzzles
6. Final thought - What is the point of education?
1. Latest interactive math applets
a. New Riemann Sums applet
 |
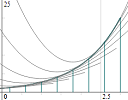I recently added a new Riemann Sums applet to IntMath. It allows you to explore the concept of finding areas under curves. Go to: Riemann Sums Applet You can see how we find areas under curves via rectangles, using an interactive applet. |
Here's some background on this important calculus topic:
b. Interactive log table and calculator
This will bring back memories for older readers.
 |
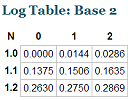A subscriber asked if I knew of a log table with 9 decimal place accuracy. (Traditionally, log books came with 4 decimal place accuracy.) I didn't, and so I created an interactive log calculator, which works in several different bases (2, e, 10, 20 and 100). You can input any (positive) value and it gives you the log value. See it at: Interactive Logarithm Table. |
There's also an interactive log table which gives output up to 9 decimal places.
You may be wondering, why create electronic log tables when the real thing disappeared 30 years ago? Well, we can still learn from exploring such tables, in a way that an ordinary calculator cannot. And I don't know too many hand-held calculators that can work in base 2, 20 and 100!
2. Context Free math-based art
Here's an idea for something interesting to do during the summer break. Create some math-based art, and learn some STEM skills in the process!
 |
Context Free is software you can use to produce some beautiful math-based art. Build STEM skills while triggering your creative side. |
3. Color Blindness graph simulator
I wrote an article a few years ago about Color blindness and math.
My main point in that article was that math teachers should make sure their diagrams, charts and graphs can be understood by the 8% or so of male students who do not perceive the full color range.
 |
The following link is to a JSXGraph graph that has different color lines, points and regions. You can use the buttons at the the top to test what the graph would look like for people with various types of color blindness. |
4. Poll results
The recent IntMath poll asked readers:
What type of math is going to be most useful for you in the future?
It looks like calculus is the most useful type of math for many of IntMath's readers, just ahead of algebra. It's unfortunate trigonometry is seen as least useful, since there are many Uses of Trigonometry.
Poll results:
| Calculus | 27% |
| Algebra | 22% |
| Financial math | 21% |
| Statistics | 12% |
| Geometry | 11% |
| Trigonometry | 7% |
Total votes: 2400
Current poll: The latest poll asks which financial math topic will have the most impact on your life.
You can respond to this poll question on any (inner) page of IntMath, for example this one: World Population Live.
5. Math puzzles
The puzzle in the last IntMath Newsletter asked about the probability of the numbers on balls in a box being relatively prime. There was only one correct answer with explanation, by Tomas. Tomas made some assumptions before tackling the problem. This is something we often need to do in "real world" math problems. Nicos' answer was close!
New math puzzle: The Phollee pyramid of ancient Egypt had a square base, but the four triangular faces were all of different shapes and size. The lengths of three of the sloping edges were 150, 160 and 200 m. The 150 m and 160 m edges were not adjacent. How long was the fourth edge?
Leave your responses here.
6. Final thought: The point of education?
For some of you, education is vital for your future. It is valued by your society and considered worthy of full effort. You feel as a result of your learning that you are growing as a person, your horizons are wider and you understand more about the world.
Sadly, for others, it is a "necessary evil", something that they need to survive when young, and get away from as soon as possible.
Arthur W. Forshay, director of the Bureau of Educational Research at Ohio State University, wrote:
"The one continuing purpose of education, since ancient times, has been to bring people to as full a realization as possible of what it is to be a human being."
What does your education mean to you?
Until next time, enjoy whatever you learn.
See the 9 Comments below.
31 Jul 2014 at 10:09 pm [Comment permalink]
The length is de square root of 200x200 plus 10x10 = 200.25
1 Aug 2014 at 1:57 am [Comment permalink]
Let ABCD the pyramid's square base and P the peak.
Let PA=160m, PB=200m, PC=180m and PD=x the unknown edge.
Then AB=BC=CD=DA, AB//CD, DA//BC and angles A=B=C=D=90deg.
Let PO the pyramid's altitude from P and O the point where the altitude intersects the square's plane.
Then we 've got four right triangles POA, POB, POC and POD.
It holds that:
PO^2+OA^2=PA^2=160^2=25600
PO^2+OB^2=PB^2=200^2=40000
PO^2+OC^2=PC^2=150^2=22500
PO^2+OD^2=PD^2=x^2
I call this set of equations (1)
Let EF the straight line from O which intersects AB at E and CD at F and it is parallel to AD and BC: EF//AD//BC.
OE is perpendicular to AB.
OF is perpendicular to CD.
OE is the altitude of AOB triangle.
OF is the altitude of COD triangle.
Besides, AE=DF and BE=CF, so: AE^2=DF^2 and BE^2=CF^2. (2)
OA^2=OE^2+AE^2 (3)
OB^2=OE^2+BE^2 (4)
from (3)&(4): OA^2+BE^2=OB^2+AE^2 (5)
OD^2=OF^2+DF^2 (6)
OC^2=OF^2+CF^2 (7)
from (6)&(7): OD^2+CF^2=OC^2+DF^2 (8)
Because of (2), (5)&(8) give: AE^2-BE^2=OA^2-OB^2 (9) and
AE^2-BE^2=OD^2-OC^2 (10)
from (9)&(10): OA^2-OB^2=OD^2-OC^2=>
=> OA^2+OC^2=OB^2+OD^2 (11)
from (1)&(11):
25600-PO^2+22500-PO^2=40000-PO^2+x^2-PO^2 =>
=> x^2 + 40000 = 25600 + 22500 =>
=> x^2 = 8100 => x = SQR(8100) => x=90m
3 Aug 2014 at 2:18 am [Comment permalink]
Hello, I thought items 1b, 2 + the link, 3 + the links were really interesting and informative. Pity about the poll result because for every day practical living and applications Trig has to be the most useful. Your final comments on Education... well I am now 71 and am still learning new things every day. I wish that the internet had been available all of my life... what an incredible resource. There really is a world at one's fingertips.Great newsletter, thanks. Best regards, Roger
3 Aug 2014 at 2:05 pm [Comment permalink]
Hi Roger: Thank you for the feedback. Trigonometry is too much of a mystery for most students, sadly - something like logarithms, I guess.
All the best with your learning!
3 Aug 2014 at 9:53 pm [Comment permalink]
I like how seeing a low poll for trigonometry you give us a trig puzzle 🙂 My trig has unfortunately rusted due to non use 🙁
4 Aug 2014 at 3:32 pm [Comment permalink]
@Chris: Actually, the puzzle can be done without trigonometry!
5 Aug 2014 at 9:10 am [Comment permalink]
The statement of the problem says nothing about the height of the "Phollee pyramid", so I would not be wrong in assuming its height equal to zero, i.e., a flat pyramid (perhaps this explains why it has never been mentioned by archaelogists). This leaves us with a plain square which has four segments (each issuing from one vertex), which intersect at a single point (the virtual top or apex of the pyramid), and the lengths of three of the segments are 150, 200 and 160 m, placed in that order clockwise (so that the 150- and 160-length are not adjacent).
Actually, only the ratios between the first and the second, and between the first and the third, lengths are important, namely 15/20 and 15/16.
The problem may be set in terms of vectors: let P be the bottom left vertex of the square base of the pyramid, and PQ and PR be two unit vectors along the bottom and left sides of the squares, respectively. The vertex opposite to P shall be called S. Let A be the intersecting point of the four vectors issuing from each vertex. The vector PA is a linear combination of PQ and PR, say a PQ + b PR. The problem consists of finding the values of a and b.
We set up two equations in terms of the norms (i.e., lengths) of the vectors joining, say, PA and QA, and SA and QA, and solve for a and b.
This may be done using Mathematica's capabilities, and the solution is a = 0.671 and b = 0.292. From here we expand to the actual length units. Since PA is 150 m, and AQ/AP = 0.601, then the length of the edge AQ is 90 m
6 Aug 2014 at 12:52 pm [Comment permalink]
About which type of math will be most useful: I know some working scientists in the biology side (cellular biology, forensices, molecular biology) and each one says she or he has not used calculus one bit in her or his work.
6 Aug 2014 at 8:16 pm [Comment permalink]
@Grag: Yes, and a lot of engineers also report something similar. But then again, others use it all the time. Depends on what you are actually working on, of course.