New Riemann Sums applet
By Murray Bourne, 26 Jun 2014
Here's a region surrounded by a curve and 3 straight lines. How do we find the shaded area?
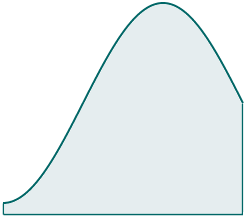
I recently added a new Riemann Sums Applet to IntMath which demonstrates some of the ways it can be done, without calculus.
Here is some background to the concept.
Background to Riemann Sums
For centuries, mathematicians tried to find efficient ways of calculating rates of change. They needed to solve a wide range of practical problems, including building faster ships, developing more accurate weapons and predicting the positions of the stars and planets for better navigation.
They were also interested in the reverse problem. That is, they may have known the rate of change, but they wanted to know the fundamental relationship between two changing quantities. For example, they may have known the velocity of an object at different times, and they wanted to know the position of the object in space during those times.
Since the age of the ancient Greeks, there were good approximation methods for such problems.
Riemann Sums
A Riemann Sum is an approximation of the area under a curve (that is, between a curve and an axis). It's named after Bernhard Riemann, the German mathematician who worked on this problem in the mid-19th century.
The principle behind Riemann Sums is simple, and was known since the time of Archimedes. (See Archimedes and the area of a parabolic segment.)
We just divide the area into smaller pieces using simple geometric shapes for which we can easily find the area, like rectangles.
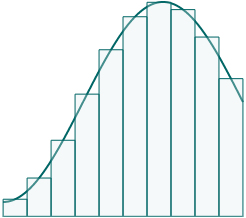
If we find the area of each rectangle, and add those areas, we'll get a good approximation for the area under the curve. If we take more rectangles, the error will reduce, and we'll get a better approximation.
We can place the rectangles in different ways (just above the curve, just below, or mid-way like in the above image).
The new applet
I recently added a new applet that allows you to explore this concept. You can change the placement of the rectangles, and you can even see how trapezoids and parabolas are used as very good approximations.
You'll find the new applet here: Riemann Sums Applet
Be the first to comment below.