Conic sections interactive applet
By Murray Bourne, 25 May 2016
I recently updated the conic sections interactive applet, part of the Plane Analytic Geometry section.
The applet now uses a different back-end meaning that it's now mobile-friendly and somewhat more convincing.
Using the applet you can explore the conic shapes that occur when you slice a double cone by a plane at various angles and positions.
You will get either a circle, ellipse, parabola or hyperbola. Such curves are called conic sections, since they are the result of slicing a cone with a plane.
Example output
When the plane's angle is less than the cone's side angle, we get an ellipse, as follows:
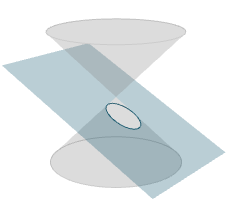
Conic section - Ellipse
If the angle of the plane is greater than the angle of the sides of the cone, the result is a hyperbola:
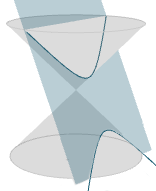
Conic section - Hyperbola
At various extremeties, you get a degenerate conic, which is either a:
- Point (e.g. when the plane passes through the point joining the two cones)
- Intersecting lines (e.g. when the plane is parallel to the axis of the two cones, and passes through the origin)
Here's an example of the latter case:
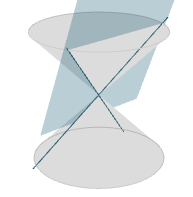
Degenerate hyperbola (2 straight lines)
Developing the interactive applet
I developed the applet using the brilliant Three.js library by MrDoob.
Constructing each of the conic section curves should have been a straightforward process of finding the intersection between the plane (at various angles) and the cone(s), then looping around the resulting curve at small intervals and joining the points.
However, each conic type threw up its own challenges. For example, I could draw the hyperbolas on the x-y (horizontal) plane, then rotate them at the correct angle and then move them into position, but the other curves didn't play nicely with that approach and I had to try all sorts of different ways.
The "fun" issue is that eah situation was multi-variable. That is, by being able to move the plane left and right, and up and down, and at different angles, a lot of testing was necessary to make sure it all worked as intended.
The math involved
There's always a lot of mathematical thinking involved in creating these interactive applets, as there is for creating any interactive visual app, especially games.
For the current conic sections applet, I needed to use and calculate:
- 3D vectors and angles
- Solving quadratic equations
- Intersection between a cone and a plane
- Trigonometric ratios (sin, tan)
- Finding square roots
- Ellipse formula
- Parabola formula
- Hyperbola formula
- Straight line formula
- Slopes of lines in 2D and 3D
- Rotation angles in 2D and 3D
- Modelling (finding a function to fit given data, e.g. for the degenerate hyperbola cases)
The link again: Conic Sections Summary Interactive
See the 1 Comment below.
3 Jul 2016 at 6:31 am [Comment permalink]
Great thing to know.