IntMath Newsletter: Pulleys, Teraplot, primes
By Murray Bourne, 02 May 2014
2 May 2014
In this Newsletter:
1. Pulleys interactive applet: math background
2. Resource: Teraplot LT
3. Math puzzles
4. Friday math movie: Falling in love with primes
5. Final thought - producer or consumer?
1. Pulleys interactive applet: math background
 |
I recently updated the pulley applet on IntMath. There was a lot of interesting math involved, and here's a description of it: Pulleys interactive applet: math background A lot of the same math is used when writing computer games. |
2. Resource: Teraplot LT
 |
Teraplot LT is a free 2D and 3D graph plotter for Windows 8 and Windows-based tablets. It's the scaled down version of the fully fledged Teraplot Graphing Software (which is a commercial product. They have a free 30 day trial). I enjoyed working with both products and found the output quality is quite good. |
3. Math puzzles
The puzzle in the last IntMath Newsletter asked about solutions for an inequality.
Correct answers with explanation were given by Peter (who provided 2 different approaches), Emily, Tomas, Francis, Nicos, Cichy and John.
(Some people just sent a number only as their answer. There was no indication of the thinking behind their conclusion.)
New math puzzle
Let's revisit the pulley applet. As explained in the article mentioned earlier, for the applet to look right, we need to know where the segments intersect with the circles.
The new puzzle is: Given 2 pulley wheels of different radius r1 and r2, with centers that are distance d apart, find the point where the first circle intersects with the segment joining the 2 circles. (The segment is tangent to each circle, and the left hand circle is centered at (0,0).) That is, you need to find the point where the red dot is.
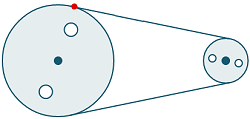
Leave your responses here.
[Hint: If you want to enter subscripts in your answer, do it like this: r<sub>1</sub>. This will come out like this: r1. If that's too troublesome, just put r1. We'll understand!]
4. Friday math movie: Falling in love with primes
 |
Comedian Adam Spencer gives us the lowdown on finding monster prime numbers. |
5. Final thought: producer or consumer?
As mentioned earlier, reader Peter gave 2 responses to the math puzzle. In a separate comment, he said:
My first response was done on an iPad. I find it hard to be wordy on that medium. The second was done on my computer with a full keyboard. That would be an interesting survey question: Are you more thoughtful (and complete) when providing an answer on a smartphone, tablet, computer, or pen and paper?
I've often thought about this. I use my phone and tablet for consuming content 95% of the time. They are good for that, but certainly not good for creating serious content, especially if it involves images and several other technologies (which my writing nearly always does.) I'll usually only respond to emails (or most other things) when I get home.
The other thing I've thought about is that as fewer people buy and use desktops and laptops, and move to mobile devices, it will mean less creators and more consumers. This is actually not good for our future.
What do you think? Please respond here.
Until next time, enjoy whatever you learn.
See the 11 Comments below.
2 May 2014 at 11:51 pm [Comment permalink]
Assume both centres (C1 and C2) lie on the x-axis.
Let (x,y) be the coordinates of the red dot and drop a perpendicular from (x,y) to the x-axis.
Extend the line joining the centres to intersect the upper segment.
Let s = the distance from C2 to the point of intersection.
Let A = the angle formed at the intersection.
Let B = the angle formed by r1 and the x-axis.
tanA = r1/(d+s) = r2/s, so s = dr2/(r1-r2)
So A = arctan(r2/s) = arctan(r2(r1-r2)/dr2)
So B = pi/2 - A
But sinB = y/r1 so y = r1(sinB)
And tanB = y/x so x = y/tanB
(Wish I could have included a figure, but perhaps this solution is too complicated anyway!)
4 May 2014 at 5:43 am [Comment permalink]
Let the big left circle's centre O (0,0), the small right circle's centre C (d,0) (OC lies on X axis), the "red" point is P (x,y) and the small right circle intersects the segment on S.
Let also, CQ the distance between C and PO, PV the distance between P and OC. Then CQ//PS, OQC, OPC, OVP and PSC are right triangles (radius is perpenticular to the tangent-segment). Also: PV=y, OV=x, PO=r1, SC=r2 and OC=d.
Then: PV^2 + OV^2 = PO^2 or y^2 + x^2 = r1^2 (1), PV^2 + VC^2 = PC^2 or y^2 + VC^2 = PC^2 (2), OV+VC=OC or x+VC=d (3), PS=QC (4), PO=PQ+QO or r1=PQ+QO (5), PQ=SC=r2 (6), PS^2 + SC^2 = PC^2 or PS^2 +r2^2 = PC^2 (7) and QO^2 + QC^2 = OC^2 or QO^2 + QC^2 = d^2 (8).
From (5)&(6): QO=r1-r2 (9)
(8)&(9): QC^2 = d^2 - (r1 - r2)^2 (10)
(4)&(10): PS^2 = d^2 - (r1 - r2)^2 (11)
(7)&(11): PC^2 = d^2 - (r1 - r2)^2 + r2^2 (12)
(2)&(12): VC^2 = d^2 - (r1 - r2)^2 + r2^2 - y^2 (13)
(3)&(13): (d-x)^2 = d^2 - (r1 - r2)^2 + r^2 - y^2 (14)
(1)&(14): (d-x)^2 = d^2 - (r1 - r2)^2 + r2^2 + x^2 - r1^2 => x = r1(r1-r2)/d (15)
from (1)&(15): y^2 = r1^2 - [r1^2] *[(r1-r2)^2]/(d^2) => y=r1*sqr{1-[(r1-r2)^2]/(d^2)}
So, P(x,y)= P(r1(r1-r2)/d, r1*sqr{1-[(r1-r2)^2]/(d^2)})
4 May 2014 at 8:39 am [Comment permalink]
I find it rather difficult to write the derivation of the answer without the help of a graph, so I give here just the plain answer - as asked in the statement of the problem:
Let u = arccos[(r1 - r2)/d], where r1 and r2 are the radii of the two pulleys (r1 greater or equal to r2), and d is the distance between the centers, with d greater or equal to 2 r1. Then, the position of the red dot is
r1 (cos(u), sin(u))
7 May 2014 at 2:05 pm [Comment permalink]
My approach was to find the slope of the belt.. This required that I find the Y Intercept as well as the length of the segement extending on the x - axis beyound the small radius. I was able to write the equation of the line (belt). Then the radius of the larger pulley intersect this line. The slope being -1/ slope of belt
Now with 2 linear eq I have x,y. For r2=2 and r1= 1/2 and distance between pulleys = 4 I get x= 0.75 and y= 1.854. I would guess that there are several easier solution to this neat problem
8 May 2014 at 7:23 am [Comment permalink]
I think it will be like many other mass-use technology shifts in that people will be surprisingly creative.
8 May 2014 at 3:51 pm [Comment permalink]
Yes, I think there is some truth on this. I use tablets only which are great for research. I am trying to learn about Astrophysics using, primarily, internet sources. When I find something I send it to myself on email and then precis the contents on hand-written one-third A4 paper slips which I then file in specific categories. Slow, but I find paper records easier to read and assimilate, and more importantly by writing it out find I get better recall... but then I am nearly 71 and my memory isn't what it used to be!
28 May 2014 at 6:02 am [Comment permalink]
(r1(r1-r2))/d, (r1(d^2-(r1-r2)^2)^(1/2))/d^2
28 May 2014 at 6:23 am [Comment permalink]
My answer at No. 7 (Suzanne Bucknell) - It looks as if I agree with Nicos Mavrommatis at No. 2, except that he has divided the d^2 of the numerator of the y co-ordinate by the d^2 of the denominator of the y co-ordinate and so he has y = (r1(1-(r1-r2)^2)^(1/2))/d^2 instead of my y = r1(d^2-... .
Both of us have eliminated references to angles by equating them to terms in r1, r2 and/or d, which are the variables given in the question and so, presumably, the answer is required to be, ideally, given in those terms only.
I vote for Nicos and me, but, as Nicos got there first (and he gave a hefty commentary on what he was doing), I think Nicos is the winner really. Perhaps I might add that I've only just seen this problem tonight (it's still only 23.22 UK time) and (honestly!) did it without reference to anyone else's answers (but I suppose you'll say 'She would say that, wouldn't she?'). Anyway, perhaps I could have just a teensy-weensy little bit of credit for having a go and getting the same as is arguably 'the right' answer?(!)
Bye for now. I hope to witter on a bit again at some later date about another problem ...
28 May 2014 at 9:24 am [Comment permalink]
@Suzanne: Thanks for the submission. As you noted, if the d^2 in the denominator for your y-coordinate was actually d, your answer would be correct.
There are no "winners" (or losers) in these puzzles! They are just for a bit of grey matter exercise.
29 May 2014 at 6:52 am [Comment permalink]
Thanks for your comment at No 9, Murray, in reply to my effort at No 8 above. Er, I didn't actually make the note you say I did, that is, I didn't actually note that if the d^2 in the denominator for my y co-ordinate was actually d then my answer would be correct.
What I said was that my answer looked as if it agreed with that of Nicos Mavrommatis at No 2 and then I explained why they were in fact the same answer even though they looked different. I guess it's the way I say it ...
By the way, if you should reply to this, Murray, I'd be glad to know if you meant what you said about the correct answer having d as the denominator of the y co-ordinate instead of d^2, as both Nicos and I had. If so, some day I'll give another look at my working to see where I went wrong - I had assumed (a dangerous thing is assumption!) my d^2 was 'right' because Nicos and I had independently arrived at the same answer and both of us had d^2 as the denominator of the y co-ordinate.
30 May 2014 at 7:50 am [Comment permalink]
@Suzanne: Using the actual number given by Don (r2=2 and r1= 1/2 and distance between pulleys = 4), your x-value turns out to be correct (x = 0.75), but your y-value expression is only correct (y = 1.854) if there was a d in the denominator, not d^2.