Lines of primes

Prime numbers have fascinated mathematicians for centuries. A prime number has exactly 2 factors - one and itself. The only even prime is 2, the rest are all odd.

The primes less than 100 are as follows:

2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

There doesn't appear to be a pattern in the distribution of primes.

How about the "gap" (spacing) between the primes? Is there a pattern in that?

1 2 2 4 2 4 2 4 6 2 6 4 2 4 6 6 2 6 4 2 6 4 6 8

There doesn't appear to be a pattern in the gaps, either.

Spiraling

Stanislaw Ulam was a Polish-American mathematician who was involved in the Manhattan Project during World War II.

One day he was bored in a meeting and began to write numbers in a spiral. He started like this, moving in a clockwise direction.

1 →	2 ↓
4 ←	3

The next round continued the "spiraling" pattern, as follows.

7	8	9	10
6	1	2	11
5	4	3	12

He kept going (it must have been a long meeting), then highlighted the prime numbers and found something interesting.

73	74	75	76	77	78	79	80	81	82
72	43	44	45	46	47	48	49	50	83
71	42	21	22	23	24	25	26	51	84
70	41	20	7	8	9	10	27	52	85
69	40	19	6	1	2	11	28	53	86
68	39	18	5	4	3	12	29	54	87
67	38	17	16	15	14	13	30	55	88
66	37	36	35	34	33	32	31	56	89
65	64	63	62	61	60	59	58	57	90
100	99	98	97	96	95	94	93	92	91

Many of the primes appear to line up when arranged in such a sprial.

Let's go much bigger and see what happens. We observe there are many places where the primes form line segments, mostly at 45°, but sometimes horizontal and vertical.

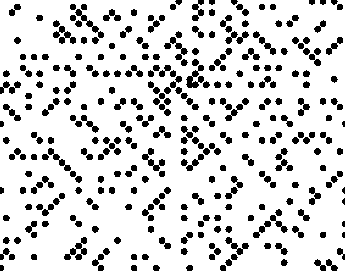
What I found interesting in the large picture is where primes are not - there are distinct blocks and patterns of white space where no primes occur.

This spiral appeared on the cover of Scientific American in March 1964 and continues to generate research interest to this day.

Why do we care about primes?

Apart from many other things, prime numbers are vital in the development of encryption algorithms, used in generating secure Internet transactions.

See the 6 Comments below.