What is trigonometry all about?

Benny is a subscriber to the IntMath Newsletter. He recently wrote:

I am going to a community college and will be taking trig next semester. So I would like to get a heads up on what I am getting into.

Well, Benny, you have taken a good first step by investigating what you are going to learn before the semester starts. Many students don't start thinking about what they are learning until the first assignment is due — and then they have to scramble around and play catch up for the rest of the semester.

The word trigonometry is from Greek and it means "triangle measure". So you'll draw and study many triangles during your study of trigonometry, especially right-angled triangles.

Uses of Trigonometry

Let's consider some of the uses of trigonometry in our everyday lives.

You will probably drive over a bridge today. That bridge was built using an understanding of forces acting at different angles. You will notice that bridges involve many triangles — trigonometry was used when designing the lengths and strengths of those triangles.

Image Source

Your car (or phone) may have an inbuilt GPS (Global Positioning System), that uses trigonometry to tell you exactly where you are on the Earth's surface. It uses the data from several satellites and earth geometry like we learned about in this IntMath Newsletter, then uses trigonometry to determine your latitude and longitude.

Image Source

You will probably listen to some music today. The song you listen to has been recorded digitally (a process that requires Fast Fourier Transforms, which use trigonometry) and it has probably been compressed into MP3 format using lossy data compression (which uses an understanding of the human ear's ability to distinguish between sounds) which also requires trigonometry.

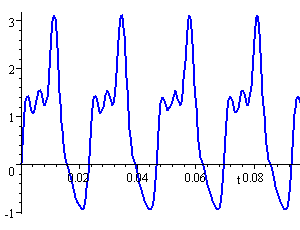
Image Source

On your way to school, you will pass a modern building. Before they built that structure, they needed to survey the area (using a leveling instrument) and then design the building (using 3-D modeling software), and determine the angle of the sun and winds (for best energy efficiency and placement of solar panels). All of these processes require an understanding of trigonometry.

Leveling instrument. Source

If you live near the sea, the tides affect what you can do at different times of the day. The tide charts that they publish for fishermen are predictions about tides years in advance. These predictions are made using trigonometry. Tides are an example of a periodic occurrence (they occur in repeating patterns. It's not exactly periodic, but close.)

Image Source: Wikipedia

In fact, trigonometry is important in almost all fields of science and engineering.

(See all the Uses of Trigonometry that are mentioned in Interactive Mathematics.)

What do you Learn in Trigonometry?

You usually start the study of trigonometry by looking at how right triangles are used to measure things that are otherwise quite difficult to measure. For example, heights of mountains and trees can be determined by the use of similar triangles. I can easily measure lengths AB and AC in triangle ABC (written ΔABC) and use that to find height DE. I could do a similar process to find the height of the mountain.

Image Source

What if the angles are different? Trigonometry allows us to use ratios that are associated with any angle ABC, so we can calculate a broad range of heights without having to measure them.

You will learn about three important ratios for any angle: sine (shortened to sin), cosine (cos) and tangent (tan). I strongly suggest that you learn these 3 ratios very well, since much of later trigonometry depends on them. (See Sine, Cosine, Tangent.)

Usually we measure angles using degrees (°) but these are not so useful for science and engineering. You will also learn about radians, which is an alternative — and more useful — unit for measuring angles. (See Radians.)

After you have mastered the basics, you will go on to learn about Graphs of Trigonometric Functions (think of the squiggles you see on an earthquake graph or a heart monitor) and then Analytic Trigonometry, which gives you a set of procedures that make it easier to solve more complex problems.

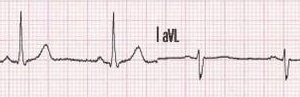
ECG of a 26 year-old patient. Source

Tips for Learning Trigonometry

a. Draw a lot: Drawing definitely helps with your understanding of trigonometry. When you need to solve problems later, it really is valuable if you can sketch the problem quickly and accurately. In particular:

1. Draw the triangles that you are studying;
2. Sketch the situation in the word problems; and
3. Practice drawing the sine and cosine graphs until you can do it without having to join millions of dots on the page.

b. Learn the basics well: By "basics" I mean:

1. The definitions of sin, cos and tan and how to use them in triangle problems;
2. The signs of trig ratios of angles greater than 90° (i.e. know when they are positive or negative);
3. The graphs of y = sin(x) and y = cos(x) (and the concept of periodic functions)

c. Take care using your calculator: The most common problems when using caculator in trigonometry include:

1. Being in the wrong mode (e.g. being in degree mode when you should be in radian mode)
2. Trusting the calculator more than your brain. The calculator will not always give you the correct sign (+ or −). Often you need to figure that out for yourself.
3. Always estimate your answer first so you can check against what your calculator tells you.
4. Make sure you know why your calculator should not use "sin^-1" or "cos^-1" on the buttons. This confuses many students and it is not necessary. We should use arcsin θ so it is not confused with 1/(sin θ)

So there you go Benny. I hope that gives you an idea of what trigonometry is used for, what it is about and what to watch out for. Sadly, trigonometry gets a bad press with many students. It doesn't need to be so if you get on top of it early and follow the above tips.

Note: This article appeared in an earlier IntMath Newsletter. Many people asked me to publish it as a separate article.

See the 16 Comments below.