IntMath Newsletter: Pedigrees, resources
By Murray Bourne, 30 Jun 2015
30 Jun 2015
In this Newsletter:
1. Pedigree collapse
2. Resource: eMathHelp
3. Resonant frequency example
4. Math puzzles
5. Math movie: How equal do we want the world to be?
6. Final thought: What employers care about
1. Pedigree collapse
 |
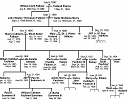How many ancestors do you have? All of us have 2 parents, 4 grandparents and 8 great grandparents. But does this go on forever? See: |
2. Resource: eMathHelp
eMathHelp is a useful collection of calculators, math lessons and practice questions, with topics ranging from pre-algrebra to differential equations.
The calculators allow you to enter your own problem, and provide clearly explained step-by-step solutions, including some color-coding to make it even easier to follow.
There's also an Online Graphing Calculator, which is quite versatile.
eMathHelp appears to be one of the better free math resources.
3. Resonant frequency example: London's Millennium Bridge
I recently enjoyed a trip to the UK. Of course, I was always on the lookout for items of mathematical interest.
For the millennium celebrations in 2000, London built the Millennium Footbridge. It spans the River Thames between St Paul's Cathedral and the Tate Modern art gallery.
London Millennium Footbridge, from St Paul's Cathedral
On opening day in June 2000, participants in a Save the Children charity walk complained of vibrations in the bridge.
It was a classic case of a suspension bridge experiencing swaying due to resonant frequency. This is the same phenomenon that allows a singer to break a wine glass just with their voice. (See this quite funny lecture where they try it out.)
As the 1000 participants walked across the bridge, their individual small vibrations tended to encourage others to walk "in tune" to maintain balance, resulting in a positive feedback loop. That is, they began to march in sync, in a lateral (sideways) sense. At its center, the bridge's sideways movement was about 75 mm at 1 Hz. [Source]
There was also a band playing at the head of the participants. I wonder if the tempo of their music had any effect in this situation.
After a few days of restricted access, the authorities closed the bridge altogether, and it took 2 years to fix the problem.
The solution involved the installation of around 90 dampers that reduce both lateral and vertical movement.
Fluid-viscous dampers (at bottom), controlling horizontal movement.
One earlier study following a similar experience on a German footbridge concluded that:
The lateral sway of a person’s centre of gravity occurs at half the walking pace. Since the footbridge had a lowest lateral mode of about 1.1 Hz, the frequency of excitation was very close to the mean pacing rate of walking of about 2 Hz. [Source]
Tacoma Narrows Bridge Collapse
When I first heard about the London case, I wondered why the designers had not incorporated lessons learned from the Tacoma Narrows Bridge Collapse in 1940.
However, it was a different situation. In that case, mechanical sideways forces were not the cause of the initial excitation of the bridge. It swayed so much due to aeroelastic flutter, and eventually collapsed.
Tacoma Narrows Bridge collapse (image source)
See video of the Tacoma Narrows Bridge Collapse.
4. Math puzzles
The puzzle in the last IntMath Newsletter asked about the length of a helix.
Correct answers with explanation were given by Jaff and Thomas.
Entering math in comments: I added a feature to make math entry on tablets or phones easier. You can use "qq" for the delimiter, since it's easier to type than the back-tick.
I messed up: Unfortunately, I had an incorrect number in that question. The circumference should have been 4 cm, not 3. This makes the problem a little easier, since we'll have a set of 3-4-5 triangles.
New math puzzle
In the Museum of the History of Science in Oxford, I came across these 2 protractors which had been collected by a mathematics teacher.
The teacher noticed his students were making incorrect angle measurements, and when he looked more closely at the protractors they were using (made in China in the mid-1990s), he found some serious flaws.
What's wrong with each protractor, and what angle would give the maximum error in each case? Can you estimate that error, based on the photos?
Leave your responses here.
NOTE 1: The protractos were actually circular, but appear elliptical in the photos due to parallax error.
NOTE 2: China's manufacturing expertise has dramatically improved since the time these were made.
5. Math movie - How equal do we want the world to be? (Dan Ariely)
 |
Wealth disparity is getting worse in most countries, and governments are right to worry about it because it can lead to social unrest. This talk by Dan Ariely, professor of psychology and behavioral economics at Duke University, challenges what we really mean by "income equality" and how it might be achieved. And yes, mathematics is involved. |
6. Final thought: What employers care about
Here's something I wrote for a training session recently. If we want to develop graduates who are useful for the workplace, we need to think about how to develop their skills, not just their knowledge.
Employers don't care what graduates know. They care more about what graduates can do with what they know, and their attitude to doing it.
Until next time, enjoy whatever you learn.
See the 7 Comments below.
