IntMath Newsletter: Headphones, Desmos, Ada, impedance interactive
By Murray Bourne, 14 Nov 2012
14 Nov 2012
In this Newsletter:
1. How do noise canceling headphones work?
2. Complex numbers interactive
3. Math tool: Desmos Graphing Calculator
4. Ada's story
5. Math puzzles
6. Friday math movies
7. Final thought - doing nothing
1. How do noise canceling headphones work?
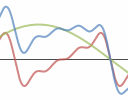 |
How can we enjoy music while traveling on noisy public transport? What is the math behind noise canceling headphones? |
2. Complex numbers interactive
A lot of students study complex numbers but have no idea how it is used in the "real world".
One of the interesting applications is in electronics. In an AC (alternating current) circuit, capacitors and inductors create a resistance, but the behavior is quite different compared to the effect of an actual resistor.
You can investigate some of these concepts here in this Interactive RLC graph. You can drag the red, green and blue sliders to change the values of the resistor, capacitor and inductor, and in turn see the effect on the impedance (effective resistance).
3. Math tool: Desmos Graphing Calculator

Desmos Graphing Calculator is a great online graphing tool since it is easy to use and has attractive graphical output. (The graphs for the headphone article above were produced using Desmos.)
I agree with Desmos' own summary:
Desmos is the next generation of graphing calculator: in-browser, beautiful, and free!
It's yet another threat to handheld calculators, but not really until all students have access to a computer and (the biggest if) if schools allow open-book, open-Web assessments.
Google Ventures was so impressed with Desmos, they recently provided $800,000 funding to expand the tool.
Desmos also works well on tablets. The link again:
4. Ada's Story

Ada was the daughter of the poet Lord Byron, but she never knew him. After suffering from measles at the age of 14, she was a sickly child and spent quite some time bedridden.
Ada was taught mathematics from an early age by her mother to "root out any insanity". She became quite good at math and developed friendships with several noted scientists of the day, including Charles Wheatstone and Michael Faraday.
Of course, in the conservative days of Victorian England, the science community was dominated by men, making it difficult for her to be taken seriously.
Later Ada became interested in phrenology (how the bumps on your head were supposed to indicate skills or personality) and animal magnetism. She also worked on a mathematical theory for how the brain gave rise to thoughts.
Who was she? Augusta Ada King, Countess of Lovelace (1815 - 1852) was an English mathematician and was regarded as one of the world's first computer programmers. She worked with the famous Charles Babbage on his mechanical computer, the analytical engine.
Ada Lovelace Day is celebrated in mid-October each year. Its goal is to "raise the profile of women in science, technology, engineering and maths" (Yes, I know I'm a bit late for 2012!).
Feel free to share your stories about any woman who has inspired you in the fields of math or science. You can do so here
5. Math puzzles
(1) The puzzle in the last IntMath Newsletter involved finding the area of an annulus (the area between 2 concentric circles).
The following people had the correct answer and showed good reasoning: Devanie, Erez, Alix, Tom, Nicos, Mawannda, and Thomas. Several others had the correct answer, but included no indication where it came from.
You may be interested to know you can answer this puzzle by considering the degenerative case. That is, if the radius of the inner circle is 0, then the shaded portion becomes the whole circle with radius 7, so the area = πr2 = 49π.
(2) Entering pi and square root: This puzzle required typing pi (π) and square root (√) in the "Comment" text box and many respondents had problems. How do you do it?
Pi is just: π
Square root sign is √
If you copy your answer from MS Word or similar, it just gives you a question mark in the comment, because the symbol is not recognized.
There is a preview option so you can see your comment before you submit it.
(3) Latest puzzle: Using a flashlight, you can send messages by making short or long flashes. How many different messages can be sent using no more than 4 flashes?
You can leave your responses here.
6. Friday math movies
 |
(a) A test for Parkinson's Here's a possible test for Parkison's Disease based on math. |
 |
(b) Triumph of the Hexagon This is a bit of light relief - hexagons to music. |
7. Final thought - doing nothing
Many math students (and sadly, teachers too) seem to put more emphasis on the mistakes they make, adding to their stress, rather than their successes. This "glass half emplty" approach helps to convince students they are dumb and can't do it. Here's one way to approach mistakes in math:
A life spent making mistakes is not only more honorable, but more useful than a life spent doing nothing. [George Bernard Shaw]
Until next time, enjoy whatever you learn.
See the 11 Comments below.
14 Nov 2012 at 2:46 pm [Comment permalink]
The number of messages that can be sent using maximum 4 flashes:
Using 1 flash= 2
Using 2 flashes = 2^2
Using 3 flashes = 2^3
Using 4 flashes = 2^4
So, total number of different messages = 2 + 2^2 + 2^3 + 2^4
= 30
14 Nov 2012 at 4:05 pm [Comment permalink]
THE ANS IS 16
14 Nov 2012 at 4:36 pm [Comment permalink]
This question requires knowlegde of permutations. there are only 2 possibilities and 4 chances, therefore the answer is 2^4= 16 messages
15 Nov 2012 at 3:32 am [Comment permalink]
More Desmos!!! I do tutoring to people who cannot afford books, tablets, computers, much less a calculator.
15 Nov 2012 at 11:30 am [Comment permalink]
The no. of messages can be sent using 1 light = 2
The no. of messages can be sent using 2 lights = 2*2=4
The no. of messages can be sent using 3 lights = 2*2*2 = 8
The no. of messages can be sent using 4 lights = 2*2*2*2 = 16
Therefore the no. of different messages that can be sent using no more than 4 flash lights = 2+4+8+16 = 30.
15 Nov 2012 at 7:26 pm [Comment permalink]
I wonder where my answer of the previous puzzle has gone to?
I don't see it anymore in the comments.
Anyway the answer to the latest puzzle:
Hypothesis 1 : Always sending 4 flashes(short and/or long)
short flash:0 ; long flash:1
0000
0001
0010
0011
....
1111
Answer: 16 or 2^4
Hypothesis 2: Sending a maximum of 4 flashes
0;1 + 00;01;10;11 + 000--->111 + 0000--->1111=
2^1 + 2^2 + 2^3 + 2^4 = 2 + 4 + 8 + 16 = 30
So the answer is 30. If You consider sending no flashes also to be a message then the answer is 31.
15 Nov 2012 at 9:15 pm [Comment permalink]
Let the long flash = "-" and the short one = ".".
Using all four flashes you may have 2^4=16 combinations: (----/---./--.-/-.--/.---/--../-.-./.--./-..-/.-./..--/...-/..-./.-../-.../....). Using three flashes you 've got 2^3=8 combinations: (---/--./-.-/.--/-../.-./..-/...), two flashes 2^2=4: (--/-./.-/..) and one flash 2^1=2:(-,.).
The total sum is: S=(2^4)+(2^3)+(2^2)+(2^1)= 30 different cases.
16 Nov 2012 at 1:15 pm [Comment permalink]
2 raised to the power 4 messages
18 Nov 2012 at 10:47 am [Comment permalink]
The number of different signals = 2^1 +2^2 +2^3 +2^4 = 30
There are 4 possible groups. Taking no flash as a non signal.
The groups are 1 Flash, 2 Flashes, 3 Flashes or 4 flashes.
Consider only all the possible combinations of LONG Flashes in each group, this includes the possibility of a no Long Flash combination.
Then the number of signals = 2^1 +2^2 +2^3 +2^4 = 30
The Base 2 signifies Long has 2 states present or absent.
The exponents represent the number of flashes in each group.
Now the tricky bit is the see that the absence of a Long
Flash in any combination is a Short Flash. Job done.
If in doubt,
the construction of 1 bit, 2 bit, 3 bit, and 4 bit
Binary Up-Count sequences will reveal the 30 different signals. Rem to start each Count at 0. A "1" signifies the presence of Long, and the "0" for its absence is then becomes a Short.
20 Nov 2012 at 7:34 am [Comment permalink]
16 messages
23 Nov 2012 at 6:42 am [Comment permalink]
2+2^2+2^3+2^4= 30
30 messages