How do noise canceling headphones work?

These days I spend quite a bit of time in trains and buses.

The ambient (background) noise level in public transport is usually quite high (on average above 70 A-weighted decibels on trains and in stations) and this has known effects on stress levels and hearing loss. [Source]

On the train, I often hear music coming from people wearing earphones. Such people like it loud anyway, but in many cases they've cranked up the volume even more to get above the train noise.

It turns out there is quite a lot of interesting mathematics involved in this situation.

Low noise levels

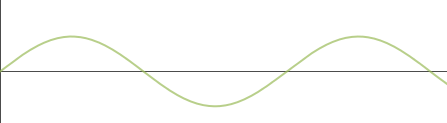
Say I'm listening to some flute music. (A pure flute note has a signal which is quite close to a sine curve.)

At home where it's quiet, I can hear every note clearly at the following volume level.

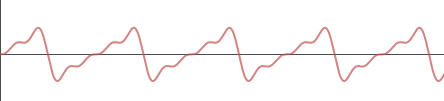
But when I get on the train, there are many loud and quite complex sounds. I've represented that unwanted noise using this red signal:

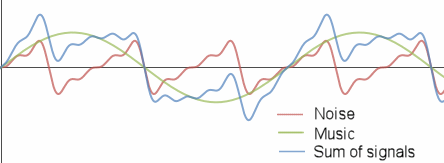
When we add that messy background noise to my flute music, we get this (the blue signal is the addition of the flute music and the background noise):

To hear the music properly I need to turn up the volume (the amplitude is now greater - that is, the wave carries more energy). Here it is, with 2.5 times the original amplitude:

(The frequency hasn't changed - we've just turned it up.)

Now we can hear the music a bit better, but there is still a lot of background noise intruding on our enjoyment.

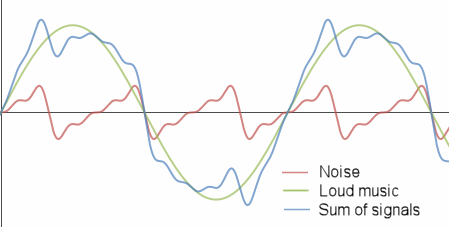
Here is the signal that's reaching our ears. It's loud, but we can at least make out the flute sound now.

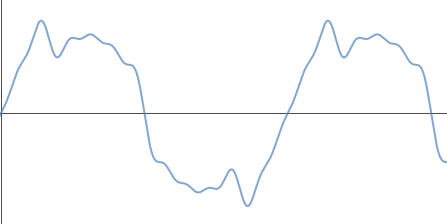
The overall sound level in our ear is now quite dangerous. With 70 dB coming from the train, plus an unknown level from my MP3 player, we are at scary levels.

WHO and EPA recommended daily allowable exposure times are 24 hours at 70 dBA, 8 hours at 75 dBA, 2.7 hours at 80 dBA, 0.9 hours at 85 dBA, and 0.3 hours at 90 dBA. [Source]

Above these levels we can expect to suffer permanent noise-induced hearing loss.

My commute is around one hour. No wonder my ears become physically uncomfortable while trying to enjoy music.

Noise Canceling Headphones

The idea behind noise canceling headphones is to neutralize the background noise. The headphones have a microphone that picks up the unwanted outside noise, analyzes it and produces a sound which is the opposite to the outside noise signal.

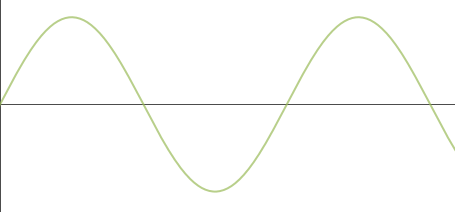
Here is the original noise signal and its negative (the reflection in the horizontal t-axis, in black):

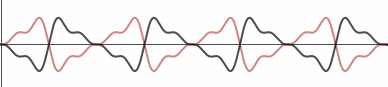
To obtain the above black signal, I just multiplied the red noise signal function by negative 1.)

When we add these 2 signals together, they cancel each other out and give us "zero" noise. We can turn down the music and hear it just like we are in a quiet environment.

Of course, in reality the headphones have to work pretty fast to perform this trick successfully, and it's not surprising it works better for low frequency sounds (because it has enough time to produce a strong negative signal) and not so well for high ones.

The headphones I have claim "more than 22 dB noise canceling at 200 Hz". It also claims "95% reduction" (whatever that really means). But it certainly is a lot better than not having them at all.

For further information and background, see Composite Trigonometric Graphs.

You may also be interested in Math of ECGs

See the 2 Comments below.