IntMath Newsletter: Finite paint, Perlin Noise, Calcpad
By Murray Bourne, 29 Mar 2018
29 Mar 2018
In this Newsletter:
1. New on IntMath
2. Resources: CalcPad and flim-flam
3. Math in the news: Computer vision
4. Math movies
5. Math puzzle: Book mark
6. Final thought: Bitcoin
1. New on IntMath
(a) The object with finite volume but infinite surface area
 |
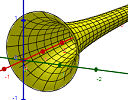This object has a strange property - we can fill it with paint, but its surface area is so large we can never finish painting it. How is this possible? |
(b) Flux - a Perlin Noise example
Continuing the Math Art in Code examples, this one uses an interesting range of mathematical concepts.
 |
Perlin Noise was an important development in computer game and animations, as it made surfaces a lot more realistic. The process is based on vectors, interpolation and differential calculus. See: |
2. Resources: CalcPad and flim-flam
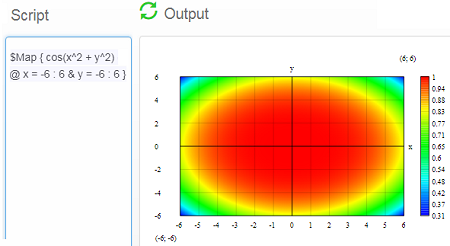
(a) CalcPad
CalcPad is a free online programmable calculator that's worth a look. Here's a screen shot:
It handles a wide range of function graphs, and its output can be saved to Word or printed.
(b) Fibonacci Flim-Flam
Donald E. Simanek, Emeritus Professor of Physics, Lock Haven University of Pennsylvania takes a swipe at the often false claims of those who see the Golden Ratio in just about everything from sunflowers to the art of da Vinci.
 |
An enthusiastic critic of pseudoscience takes a closer look at what doesn't conform to the Fibonacci sequence and the Golden Ratio. See: |
3. Math in the news: Better computer vision
I'm a big fan of the idea of driverless cars, but there was a tragic accident last week where a pedestrian was killed because the car didn't "see" her. We need better computer vision at night and in fog.
 |
MIT recently announced a successful trial of an improved computer vision system using statistics. See: |
4. Math Movies:
Here are two recent math-related videos:
(a) Algorithms: weapons of math destruction?
 |
There's a lot of talk at the moment about how Cambridge Analytica used Facebook data to sway the 2016 US election. Are big data algorithms fair and unbiased? Cathy O'Neil doesn't think so. |
(b) Where do math symbols come from?
 |
I have great empathy for the struggles students have regarding math symbols. Here's an overview of why we use them and where some of them come from. |
5. Math puzzles
The puzzle in the last IntMath Newsletter asked about the sum of the digits of a particular number.
Correct answers with explanation were given by: Twinomugisha, Thomas, Chris, Getnet, Tom Barrett, JDK, Tomas, and Tom Polak. Most of the solutions used the approach of observing what happens with low powers of 10, then extrapolating.
Good on those of you who used the math input system! (Just a note: If you create your math expression in Microsoft Word then copy into the math system you will encounter problems. Best to type it in directly.)
New math puzzle: Lost book mark
In the old days when people read books (^_^), they used a book mark to remember where they were up to. Pedro was reading 4 books and his book mark was left in one of them. What is the expected number of books he needs to open in order to: (a) Find the book mark, and (b) Know which book the book mark is in?
You can leave your responses here.
6. Final thought: Bitcoin power consumption
The blockchain continues to fascinate people and consume large amounts of media coverage. Electronic currency does have a cost, however - the vast computing resources required to "mine" a new coin require a lot of energy. Alex de Vries started the ball rolling with some eye-watering estimates, and pri.org tries to make sense of it all. Their conclusion:
The most current and widely cited estimates put bitcoin’s yearly energy use at somewhere between 4 and 35 terrawatt-hours. To put that in perspective, all of Google used about 5.7 terrawatt-hours in 2015. [Source: pri.org]
[Hat-tip to Suzanne Bucknell and PiPo for alerting me to some of the items in this Newsletter.]
Until next time, enjoy whatever you learn.
See the 3 Comments below.
