IntMath Newsletter: Computational essays, random numbers
By Murray Bourne, 24 Apr 2018
24 Apr 2018
In this Newsletter:
1. New on IntMath
2. Resources: Computational essays
3. Math in the news: Random numbers
4. Math movies
5. Math puzzle: Parking
6. Final thought: Eating plastic
1. New on IntMath
(a) Updated CO2 graphs
As an example of composite trigonometric graphs, I model the weekly CO2 concentration data as observed in Mauna Loa, Hawaii. I used to create a static graph from time to time, but it was tedious and since the NOAA data is updated regularly, it would become quickly out of date.
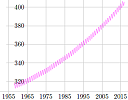 |
So now it makes use of an SVG (scalar vector graphics) image, using the latest data obtained from the NOAA site. |
You may also find the interactive spring activity on that page interesting.
(b) Math Art in Code: Moiré effect
The Moiré pattern is the shimmering effect we see when a repeated pattern (like stripes on a shirt) interact with other similar patterns that are slightly out of phase.
 |
This animation illustrates Moiré effect. It involves quite simple CSS, and no javascript. |
2. Resources
(a) Computational essays
Stephen Wolfram, of Mathematica and Wolfram|Alpha fame, has proposed the idea of a computational essay. Such an essay is interactive, and has great potential for expressing mathematical and scientific concepts more clearly. It has become easier recently to develop such essays.
 |
A computational essay not only contains text and fixed images, but it can contain interactive content that can calculate math expressions, or import and manipulate data. |
You can author a notebook in the native Wolfram Desktop application (Mac, Windows, Linux)—or on the web through any web browser, or on mobile through the Wolfram Cloud app. Then you can share or publish it through the Wolfram Cloud, and get access to it on the web or on mobile, or download it to desktop or, now, iOS devices.
(b) 10 Award-Winning Optical Illusions and Brain Puzzles
One of the first things you learn in psychology is that your perception of the world is not (necessarily) the same as mine. We all construct a "best guess" at the meaning of what we are looking at, and illusionists make the most of this to trick us.
 |
These optical illusions come from Champions of Illusion: The Science Behind Mind-Boggling Images and Mystifying Brain Puzzles. Go to: |
3. Math in the news
a. Truly random numbers?
We rely on random numbers a lot, especially for good security on our digital communications. But computers are not very good at producing truly random numbers, it seems.
Any gambling system to be fair needs to be random, but this table for Drawn number frequency for the Singapore Toto shows big discrepancies in frequencies (almost twice the frequency for ball number 46 as for ball 45!).
Up to now, most random number generators are either software- or hardware-based. Neither has produced "truly" random numbers.
 |
Quantum methods: What if we use some "spooky action at a distance" (as Einstein called it)? |
According to the article, using quantumn approaches provides a superior source of randomness...
... because measurements of some quantum particles (those in a "superposition" of both 0 and 1 at the same time) have fundamentally unpredictable results.
I came across this masters thesis which looked at how good the random number generation process is in Android phones: Analysis of Android Random Number Generator (PDF, 84 pages).
b. IBM research projects: 5 in 5
Here are "5 innovations that will change our lives in the next 5 years", according to IBM researchers.
 |
The stories include the use of 3D microscopes to clean the oceans, articifial intelligence and quantum computing. See: Five innovations that will help change our lives within five years |
4. Math Movies
(a) OK Go Sandbox - One Moment of Math
OK Go is probably best known for their brilliant one-take music videos, involving extraordinary coordination..
 |
In "One Moment of Math", we get some insights into the math behind how they designed and implemented the video for The One Moment, released in 2014. |
Here's the original music clip: OK Go - The One Moment
(b) How many ways are there to prove the Pythagorean theorem? (TED-Ed)
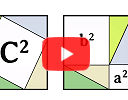 |
There are several ways ti prove Pythagoras' famous result regarding right angled-triangles. This may give you some new insights. See: How many ways are there to prove the Pythagorean theorem? |
I liked the quote at the beginning of this video:
"Reason is immortal, all else is mortal." [Pythagoras]
5. Math puzzles
The puzzle in the last IntMath Newsletter asked about a lost book mark.
There was one correct answer with explanation, given by StevieX.
New math puzzle: Parking
A city block has 12 parking meters in a row. Eight of the parking spaces are occupied by cars. A bus requiring 4 parking spaces is trying to park. Assuming the car drivers chose their spots at random, what is the probality the bus will be able to find a suitable space?
You can leave your responses here.
6. Final thought: Eating plastic

Plastic waste. [Image source]
Most of us have some seafood in our diets. With an estimated 275 tonnes of plastic waste generated worldwide and 10 million tonnes of that washing offshore per year [source], it's likely that we're eating some of it every time we eat seafood.
Litterati is an organisation whose mission is to tackle the problem of litter "one piece at a time". They provide an app that you can use to photograph and tag litter in your own environment. This is a useful piece of data collection and can be a good class project. As Litterati says:
Geotags provide insight into problem areas, while keywords identify the most commonly found brands and products. This data will be used to work with companies and organizations to find more sustainable solutions.
Earth Day was this week. Let's not wait for politicians to do something meaningful about the world's serious environomental problems - let's start doing it ourselves.
[Hat-tip to PiPo for alerting me to some of the items in this Newsletter.]
Until next time, enjoy whatever you learn.
See the 8 Comments below.
24 Apr 2018 at 8:15 pm [Comment permalink]
The answer is 1/55
explanation:
there are 9 possible sets of consequent 4 meter stretches for the bus to be able to park.
For each of this possible set, there are 8 remaining parking meters which can be filled by 8 car drivers. the possible number of ways for this is 8P8 = 8! (factorial).
so, for a total of 9 sets, the total number of possibilities of car parking are 9*8! = 9!
now, coming to total possibilities of parking for 8 cars in 12 parking meters are 12P8 = 12!/4!
so, the probability for the bus to find a parking place = 9!/(12!/4!) = 1/55
Note: here, it is assumed that the car drivers are not biased while parking the cars.
24 Apr 2018 at 11:09 pm [Comment permalink]
9/2^12
25 Apr 2018 at 12:07 am [Comment permalink]
Since bus will need four consecutive parking meters which can be done in 9 ways for example( 1,2,3 4),(2,3,4,5)........(9,10,11,12) and total no of ways of choosing four parking lots out of 12 can be done in 12 C 4 ways which is equal to 495 ways. Therefore probability that bus will get required parking place equals to 9/495=1/55
25 Apr 2018 at 8:49 am [Comment permalink]
Pythagoras. If you resolve the hypotenuse into mutually perpendicular but extremely small lines each one parallel to one of the other sides, thus creating steps in the hypotenuse, you end up with what at the macro scale produces the Pythagorean equation but if one can walk this hypotenuse at the the extremely small scale compared with the size of the triangle one finds that Pythagoras doesn't work. Comes from working to work in a CBD built on an orthogonal grid pattern.Pythagoras' next step should have been calculus.
3+4+5=12. 12 inches to the foot. One wonders if Mediaeval British architects carried around a handy bit of string, measured out in twelve units using the top part of the thumb,instead of set squares?
25 Apr 2018 at 10:03 am [Comment permalink]
@Bob: yes, this is what I was getting at in the article Taxicab Geometry.
An interesting dilemma, indeed.
28 Apr 2018 at 9:24 am [Comment permalink]
The number of possible arrangements of eight cars in 12 spaces is 12!/(8! 4!). Among these, a row of 4 empty spaces can start in position 1, in position 2, etc., up to position 9; i.e., there are only 9 arrangements which leave enough space for the bus to park. Therefore, the probability sought is 1/55 = 0.0181818...
An unpleasant feature of problems in probability is that it is often impossible to check if a solution is correct, leaving the practitioner with a feeling of doubt about his result. Fortunately, nowadays one can resort to computer experimentation techniques in order to model the problem and simulate the situation with relative ease.
For this particular problem, I made a computer simulation repeating the experiment 1,000,000 times, which took less than 15 seconds, and found that the estimated probability that the bus would find space to park is 0.018174. This dispelled any doubts about my result above.
1 May 2018 at 4:35 am [Comment permalink]
Site is very educative and motive
3 May 2018 at 4:16 pm [Comment permalink]
For the puzzle, we need to know how many arrangements are possible for the 4 remaining spaces and how many of these arrangements are consecutive as needed for the coach to park. It's easy to see the number of consecutive arrangements is 9 (1-2-3-4, 2-3-4-5.. ...9-10-11-12). The total number of arrangements possible is the combinations for 4 from 12 = 12!/(4!8!) = 495. (We need combinations, not permutations because the ordering is unimportant, eg 1-2-3-4 equivalent to 3-1-4-2 etc).
Probability that coach can park = (no of suitable arrangements)/(no of possible arrangements) = 9/495 = 1/55 = 0.0182