IntMath Newsletter: Complex numbers, evolutes, parabolas

23 May 2018

In this Newsletter:

0. Privacy, cookies and ads
1. New on IntMath: Complex numbers and Evolutes
2. Resources: names, terminology
3. Math in the news: parabolas, curiosity
4. Math movies
5. Math puzzle: Lucky numbers
6. Final thought

0. Privacy, cookies and ads on IntMath

Like most sites, IntMath could not function without advertising. As part of the advertising process, companies track your interests using cookies, so they can offer you products and services you are more likely to be interested in. This necessarily results in a loss of privacy. The new European GDPR laws come into effect this week (on Fri 25th May) and all Web publishers need to update their privacy agreements with their users.

When you next go to any page on IntMath, it will ask you if you agree to the privacy and cookie policies. I hope you are OK with them, and will continue to find IntMath useful.

1. New on IntMath

(a) Graphical explanation of multiplying and dividing complex numbers

Complex numbers certainly seem to have some weird properties, especially on first meeting. It's not always clear what we're doing when we multiply and divide them.

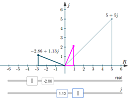This interactive applet visually explains the process of multiplying and dividing complex numbers. See: Graphical explanation of multiplying and dividing complex numbers

(b) Math Art in Code: Evolute animations

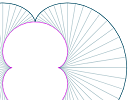An evolute of a curve is the path traced out by the centers of the radius of curvature of the curve. Animations of this concept produce pleasing geometric shapes. To see what all this means, go to: Evolute of a curve

2. Resources

These two resources have a cultural theme.

(a) What's in a name?

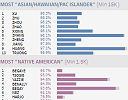Using data from the 2010 U.S. Census, Mike Cisneros visualizes surnames and self-reported races. You can search for your own surname to see the racial distribution. Go to: Surnames and Race in the U.S.

(b) US vs UK math terminology

The above title demonstrates one of the many differences between US and UK terminology (in the US, the abbreviation is nearly always "math", whereas in British English, it's usually "maths".)

US math teacher Ben Orlin taught in England for a while and experienced some interesting communication challenges. See (in his delightful MathWithBadDrawings blog): US vs. UK: Mathematical Terminology

I related closely to this article, having grown up with British terminology, and then taught in Asia (where you find a mix of US and British math terminology) for many years.

3. Math in the news

(a) Using semi-parabolic reflectors for better energy efficiency

The parabola is a much-studied curve in mathematics, due to its many useful properties and applications.

In this recent article from PhysOrg, we read how energy efficiency was improved for a headlight by using two half-circular parabolic reflectors. See: Powerful LED-based train headlight optimized for energy savings

For more background, see the Parabola page within the Plane Analytic Geometry chapter.

(b) Curiosity and success in math

A lot of educational research ends up stating what appears to be the bleeding obvious. This study by Prachi Shah at the University of Michigan concluded that "the kids’ reading and math scores were consistently better the more curious they were". No surprises there.

The challenge I kept thinking about when reading the article was how to instill, encourage and improve curiosity levels? For most students, this isn't achieved by completing yet another worksheet.

See: Researchers have isolated what may be the single most important trait that makes kids successful in school

4. Math Movies

(a) Paying kids to do their math homework

"So how do we motivate students to learn math?" This is a very common question I get from young (and not so young) math teachers.

In this video, we hear one company's approach is to pay students to do their homework. See: This company pays kids to do their math homework

This idea surfaces from time to time. I'm not sure I'm that comfortable with it (since I feel the best motivator is satisfaction from successfully achieving something that was challenging, rather than extrinsic rewards), but it's interesting to consider.

You can learn more about Jebara's company here: Mathspace.

(b) How did Polynesian wayfinders navigate the Pacific Ocean?

We often feel the ancients were "primitive" and knew very little. However, the ways the Polynesians managed to migrate around the Pacific were very impressive. See: How did Polynesian wayfinders navigate the Pacific Ocean?

5. Math puzzles

The puzzle in the last IntMath Newsletter was about bus parking probability.

Correct answers with explanation were posted by Eamon, Tomas, Vijay and Saikrishna.

Tomas mentioned in his answer that it's great to be able to check our answers to such problems using computer simulations. I agree!

New math puzzle: Lucky numbers

In a particular game, "lucky" numbers are defined as the remaining integers after doing the following steps:

1. List all the positive integers in ascending order
2. Set n to 2
3. Delete every n-th integer from the existing list
4. Now increase n by 1
5. Repeat steps 3 and 4.

What is the 5th lucky number?

You can leave your response here.

6. Final thought

There are way too many instances of corruption in the world today. This proverb gives us a context.

"When money speaks, the truth is silent." [Russian proverb]

[Hat-tip to various contributors who alerted me to certain items in this Newsletter.]

Until next time, enjoy whatever you learn.

See the 3 Comments below.