Math in cross-wind landing vectors applet

I recently updated the cross-wind landing applet, which is an introductory activity for the section on adding vectors in 2 dimensions in the Vectors chapter. The applet now works on tablet devices.

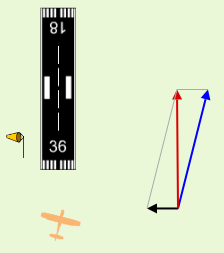
Here's a screen shot of the applet:

Pilots need to be very aware of the effects of wind in all stages of flight - from takeoff (where they need to point into wind), during flight (where a tail wind means you get there quicker, so it's cheaper) and during landing (where once again, you need to land into wind, and if there is a cross wind, it can make the landing a bit more challenging).

Flying is an interesting real-world application of vector addition.

The cross wind applet

The idea behind this applet is that students should be given an opportunity to investigate mathematical concepts with some real-life (or simulated) activity. By thinking about what they have discovered, they are more likely to be able to connect the dots when it comes to later applications.

The applet encourages you to fly around and to land the Cessna with a significant cross wind.

You'll hopefully notice that you travel across the ground much faster when the wind is behind the aircraft (2 positive vectors added together), and slower when the wind is towards you (addition of one positive and one negative vector).

There's some interesting math going on in the programming behind the applet, so let's have a look at some of it.

Trigonometry

Velocity vectors in 2 dimensions are made up of 2 components - one vector in the x-direction (usually written v_x) and the second in the y-direction (usually written v_y).

To move the aircraft around, I used the following code:

xspeed = Math.cos((90-dir)*Math.PI/180)*speed + wind;
yspeed = (Math.sin((90-dir)*Math.PI/180)*speed);

where:

xspeed = v_x (the x-component of the velocity)

yspeed = v_y (the y-component of the velocity)

dir = the direction the plane is heading, in degrees (In navigation, 0° = North and is at the top of the graph, and angles are measured clockwise)

speed = the airspeed of the aircraft

wind = the magnitude of the wind (In the applet, since the wind is from only due East or due West, we only need to add the wind component to xspeed.

In javascript, the trigonometric functions are calculated using radians, while my input angle "dir" is in degrees.

So I needed to convert my degrees to radians by multiplying by pi and dividing by 180.

The above 2 lines just work out the 2 components of the vector, and move the aircraft to the appropriate position in time.

Vectors

Of course, I'm using the concepts of vector addition throughout the applet.

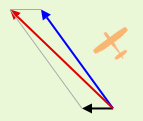
In the above screen shot, the Cessna is pointing in the direction of the blue vector (this is called the aircraft's "heading"). The wind is from the East (the black vector) and the result is the plane is moving across the ground in the direction of the red vector.

Notice the red (resultant) vector is longer than the blue (heading) vector, and this represents greater speed. The wind is helping in this case, as it is behind the plane, but at an angle. We work out the size of this resultant vector by using the parallelogram you can see in the diagram.

In this next screen shot, we see the wind is blowing from due East, and the aircraft is trying to head East, but is being slowed down resulting in a shorter resultant vector.

Next, we see the case when the wind is behind us (from the West) and it is helping us (the resultant vector is longer).

No matter what direction the plane is pointing, the length of the blue vector is constant, since the plane's airspeed is constant in the applet.

The point at the end of the blue vector follows the path of a circle in polar coordinates,

(r cos θ, r sin θ)

where r is the radius of the circle, and θ is the angle at the center of the circle.

Absolute value

To determine whether the Cessna is close to the landing spot (the number "36" at the end of the runway), and pointing in an appropriate direction for a landing, I used this expression:

if(Math.abs(cessX) < 2 && Math.abs(cessY - 65) < 3 
  && (dir < 30 || dir > 330) ) {
 ... 
}     

where

cessX = the current x-position of the aircraft

cessY = the current y-position of the aircraft

The expression "Math.abs(cessX)" means "find the absolute value of the current x-position". It then tests if that value is less than 2, and if it is, regard it as an acceptable value for the landing.

Another way of writing this (using normal math notation) is:

| cessX | < 2

and this means

−2 < cessX < 2

That is, we can be within these limits for a landing (we will be on the runway).

As for the y-value, we have:

Math.abs(cessY - 65) < 3

(The start of the runway is 65 units from the origin point in the applet.)

In normal math notation, this is:

| cessY − 65 | < 3

We could write this as:

62 < cessY < 68

This means as long as we are lined up and pass close enough to the end of the runway, we'll land OK.

For the direction, we have:

dir < 30 || dir > 330

The 2 vertical lines "||" mean "or" in most programming languages.

Mobile device considerations

Most smart phones and tablets have accelerometer sensors which determine the tilt angle of the device in 3 dimensions, relative to when the device is lying flat on a table.

(See more on the 3-dimensional coordinate system.)

These angles (usually denoted alpha, beta and gamma) are measured in the up-down, left-right and rotate-left, rotate-right directions.

I'm using one direction only to change the direction of the aircraft when used on a tablet. It's the "beta" direction, which roughly correspnds with a "steering wheel" movement of the tablet.

window.addEventListener('deviceorientation', 
  function(eventData) {
    tilt = eventData.beta;
  } 

It's not as smooth as I'd like, but it works OK - albeit rather slowly on a tablet.

Conclusion

Math education should be less about plugging numbers into formulas and should get students to investigate phenomena through an activity. This cross wind landing applet aims to do just that. Students get the concepts (through some light-hearted activity) before worrying about the algebra.

See the 2 Comments below.