IntMath Newsletter: Reflecting graphs, data and efficient lawn mowing
By Murray Bourne, 25 Jul 2011
26 July 2011
In this Newsletter:
1. How to reflect a graph through the x-axis, y-axis or Origin?
2. Visual.ly data visualization
3. Resource: Thinkfinity
4. Friday math movie: Time to re-design medical data
5. Mow your lawn efficiently - use math!
6. Puzzles
7. Final thought: Greatness
Please note: During the northern summer break (while most math students and educators are at the beach, summer camp, working or mowing lawns), the IntMath Newsletter is published once per month.
1. How to reflect a graph through the x-axis, y-axis or Origin?
Suitable for: Everyone
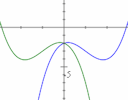 |
A reader asks how to graph f(-x) and -f(x), and what does it mean? How to reflect a graph through the x-axis, y-axis or Origin? |
2. Visual.ly data visualization
Suitable for: Everyone
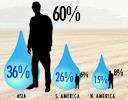 |
Visual.ly is a neat new data visualization tool. Worth a look, but it's still new. This could be a great tool for class projects in math. |
3. Resource: Thinkfinity
It appears this one has disappeared.
The resources I've been sharing in this space over the last several IntMath Newsletters was based on "Ten great sites with free teacher resources" from e-School News.
4. Friday math movie: Time to re-design medical data
Suitable for: Everyone
 |
Here are 2 videos that talk about how personalized patient data in visual form has immense implications for human health. |
5. Mow your lawn efficiently - use math!
Suitable for: Everyone
 |
This is a fun article from Australia's The Age newspaper. It describes how you can use geometry to optimize your effort. A Victa-ry for mathematics [no longer available] |
6. Puzzles
Last mail I posed the question "Can you use five 5s to make 100?".
Here's one possible solution:
(5 - 5/5) × 5 × 5 = 100
Did you get any other answers?
Here's a new one:
"My husband's age," remarked a lady the other day, "is represented by the figures of my own age reversed. He is my senior, and the difference between our ages is one-eleventh of their sum." How old are they?
7. Final Thought: Greatness
The world's best discoveries were made along a road littered with wrong turns, insufficient knowledge and many outright failures. Don't worry if you feel like that in math class sometimes!
If at first you don't succeed, you're like everyone else who went on to greatness. [Patrick Combs]
Until next time, enjoy whatever you learn.
See the 8 Comments below.
25 Jul 2011 at 10:32 pm [Comment permalink]
I find your e-letters better and better as time goes by. Thanks for sharing,
Elena
26 Jul 2011 at 6:03 am [Comment permalink]
My solution to the " 5 5s to make 100" was simply:
5 x 5 x 5 - 5 x 5
My approach to the ages problem was as follows.
Let the digits of their ages be x and y
Husband's age is 10x + y and wife's age is 10y + x
Difference in ages = (10x + y) - (10y + x) = 9x - 9y
Sum of ages = (10x + y) + (10y + x) = 11x + 11y
So 9x - 9y = (11x + 11y) / 11 or 4x = 5y
Since x an y are integers <10 x = 5 & y = 4. Ages 54 & 45
27 Jul 2011 at 3:24 pm [Comment permalink]
Well sir, i like very much what you write in the final thoughts. You think great.... Even if i am very busy, i see your final thoughts and get inspired from the quotes of the great people. Long live. Hope you will continue this...
27 Jul 2011 at 7:49 pm [Comment permalink]
I'm glad you find them inspiring, Muaz!
28 Jul 2011 at 2:49 pm [Comment permalink]
Dear sir, I am in need of solution of a mathematical solution of a problem in calculus.Please help me . Problem : To find the total length of a flat spiral having outer end radius= 15.5 units, inner radius=5 units & the increase in radius per turn=0.81 unit, the total No. of turns in the spiral is 7.5 . Thank you .
29 Jul 2011 at 12:58 am [Comment permalink]
Goodevening dear sir.I am greatful with you,you write me continuously math articles.Which are important to learn mathematics.I hope i will receive such precious articles continuously in coming days.Once again i want to give you many thanks.
2 Aug 2011 at 1:21 am [Comment permalink]
Puzzle of the ages of a couple:
I tried to solve the puzzle mechanically as under.
Let the two digits of their ages be 'a' and 'b'. Then 10a+b is the age of one of them and 10b+a is the age of the other.
The sum of the ages of the two =(10a+b)+(10b+a)=11a + 11b
The difference between the ages =(10a+b)-(10b+a)= 9a - 9b
11(9a-9b)=11a+11b
9a-9b = a+b (Dividing both sides by 11)
8a=10b
4a=5b a:b =5:4.
It is evident from the puzzle that the ages are of two digits and the only possible ages in the above ratio are 54 and 45
27 Sep 2011 at 9:11 am [Comment permalink]
Hi Anantha. I replied to your question in this post: Length of an Archimedean Spiral.
I hope it helps!