When does log(x-3) = log x - log 3?
By Murray Bourne, 26 Oct 2013
I recently had a Twitter exchange with Pat Ballew who tweets using the handle @OnThisDayinMath.
I've never liked aspects of logarithm notation, and my tweet that day pointed out that despite having this convention in math:
7(x − 3) = 7x − 21,
it happens that
log(x − 3)
is mostly NOT equal to
log(x) − log(3).
Such inconsistencies in math notation cause unnecessary confusion for new learners. (See more on this issue at Towards more meaningful math notation.)
Here's the Twitter exchange:
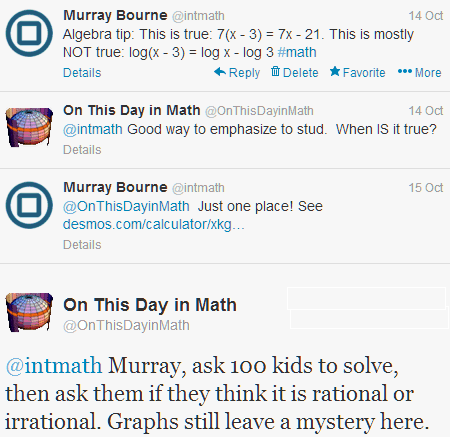
My reply
My reply contained a link to a Desmos graph showing where the graphs of y = log(x − 3) and y = log(x) − log(3) intersect.
You only really understand many math problems if you can do them graphically, algebraically, and numerically. But I get most understanding from a graph.
First let's see a graphical solution for this problem.
Graphical solution
One way of solving equations is to graph the left and right sides, and look for where the graphs intersect, since that gives us the solution.
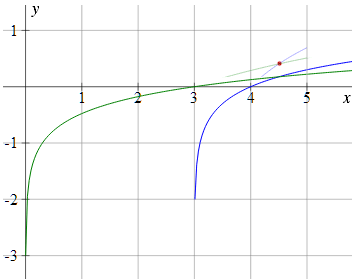
The graph I pointed to in the link was something like the following, where the green curve is y = log(x − 3) and the blue curve is y = log(x) − log(3):
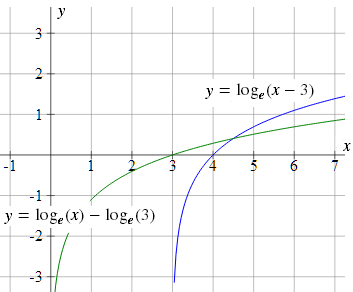
Zooming in on the intersection point, we can see the 2 curves cross when x = 4.5, and the y-value is about 0.4 (actually, it's loge(1.5) = 0.405465...).
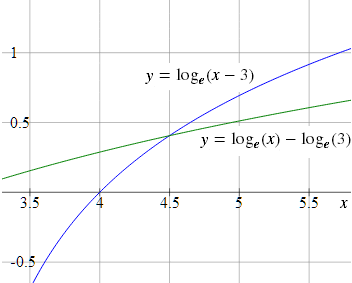
I answered Pat's question with a link to a graph as I felt that trying to explain the solution algebraically within the limitations of a 140-character tweet would be somewhat problematic.
Graphs a mystery?
I've been thinking about Pat's comment that graphs "still leave a mystery here".
I spent most of my student days and early teaching life solving equations algebraically. That's what most textbooks did, and that's what the curriculum required, so we just went ahead and did it that way. We didn't have access to computer graphing tools (or calculators early on), so there wasn't much option - algebraic solutions were quicker than drawing graphs by hand or finding numerical solutions.
Most of the time I didn't have much of a "feel" for what was going on when the equations became more complicated.
I certainly had a feel for the solution when solving linear, quadratic and other polynomial equations. If the number of terms in the polynomial was small, and it was a "nice" polynomial equation where the number of roots was equal to the degree of the polynomial, all was fine.
But then as things became more complicated, you needed a better understanding of what was happening so you wouldn't miss some of the possible x-values. For me, that understanding came from graphs.
For example, once we started doing trigonometry I didn't understand why there would be an infinite number of solutions for this equation:
sin 3x = 0.47
However, once I saw the graph of y = sin 3x, and noted where it intersected with the graph of y = 0.47, it was immediately obvious there were many solutions.
Algebraically
Back to the log question. Let's now see how to solve our equation algebraically.
log(x − 3) = log x − log 3
Using the 2nd log law on this page, we know we can write the difference between 2 logs as:
log a − log b = log a/b
So the right hand side of our equation can be written:
log x − log 3 = log (x/3)
Our equation has become:
log(x − 3) = log (x/3)
Since there are 2 log expressions with the same base that are equal to each other, we know the expressions in brackets must be equal, so we have:
x − 3 = x/3
Solving gives:
3x − 9 = x
2x = 9
x = 4.5
So assuming base e, the following is true:
log(4.5 − 3) = log 4.5 − log 3 = log 1.5 = 0.405465...
Numerically
We set up a table of values as follows.
If we try any negative value of x, we get an error. Similarly, for log(x - 3), positive values of x give us trouble unless x is bigger than 3.
| x | log (x − 3) | log x − log 3 |
|---|---|---|
| 2.5 | ?? | −0.18232 |
| 3.0 | ?? | 0 |
| 3.5 | −0.69315 | 0.154151 |
| 4 | 0 | 0.287682 |
| 4.5 | 0.405465 | 0.405465 |
| 5 | 0.693147 | 0.510826 |
| 5.5 | 0.916291 | 0.606136 |
| 6 | 1.098612 | 0.693147 |
| 6.5 | 1.252763 | 0.77319 |
| 7 | 1.386294 | 0.847298 |
| 7.5 | 1.504077 | 0.916291 |
It looks like we have found the only solution, x = 4.5.
The problem with numerical methods, like a lot of algebraic methods, is we are left wondering if there are any more solutions. You often get caught by not considering other values.
Conclusion
We've now solved the equation graphically, algebraically and numerically.
I find I get the best insights into the problem when I can see it, and so most of the time these days I choose to solve equations by drawing a graph (using computer graphing mostly.)
It's quick, and it gives me the best feel for the meaning of what I've found.
Final comments
(1) Different log bases
Does it matter which logarithm base we are using? Do we get the same x-value?
Above I was using base e (the natural logarithms). Here is the graph if we are using base 10.
Base 10
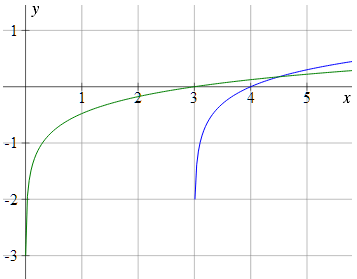
We can see the intersection point is when x = 4.5, but the resulting y-value is lower.
Base e and Base 10 solution comparison
In the following graph, we can also see where the base e graphs intersect (in lighter colors) and the log (base e) value is shown with a red dot.
(2) Alternative graphical approach
We could have also approached this problem by getting everything on the left side of the equation, as follows:
log(x − 3) = log x − log 3, when
log(x − 3) − (log x − log 3) = 0
That is:
log(x − 3) − log x + log 3 = 0
Here's the graph of y = log(x − 3) − log x + log 3
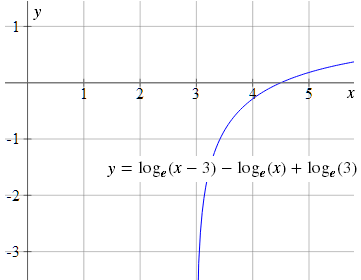
We can see it cuts the x-axis at x = 4.5, and this is our solution.
But this doesn't give us as much "feel" about what's going on as the graphs given at the beginning of this article, where we graphed both sides of the equaiton separately and then looked for the intersection.
(3) ln x or loge x?
I think "ln x" is terrible notation for natural logs. I have used loge x throughout this article as it is much easier to identify that it is a logarithm expression, and so easier to understand. I ranted about this issue in Logarithms - a visual introduction.
See the 12 Comments below.
26 Oct 2013 at 8:56 am [Comment permalink]
Murray, I agree with the triple pronged approach to teaching (and learning) using graphs, numerical approaches and analysis, but I think when you see the graph you see large features (sin(3x) has lots of solutions for values between -1 and 1) and log (x-3) is only equal to log(x)-log(3) once
BUT, the graph shows that they intersect at ABOUT (4.5, 0.4) and only with the analytic solution do we see that one of these coordinate values is rational, and one is not. ) No matter how much we zoom, we can never see it is EXACTLY anything....
But I love your approach in its entirety.
26 Oct 2013 at 10:20 am [Comment permalink]
Hi Pat
A few quick mouse scrolls in Desmos gives me this:
I can see the x-value is "very close" to 4.5 - within 5 decimal places, and the y-value is 0.405465 to 5 decimal places.
These were the values we were happy with earlier.
No algebra required!
27 Oct 2013 at 1:05 am [Comment permalink]
Hi Murray, I have to side with Pat on this. The graphical approach certainly adds a lot to our understanding of what it means to solve the equation, but what "we" were happy with has nothing to do with whether we really had the *exact* answer. And the only way to be sure of that is with the algebraic approach, which I think does fit quite nicely in a tweet ("Taking exp of both sides gives x-3=x/3 which easily gives x=9/2" should be enough)
27 Oct 2013 at 12:54 pm [Comment permalink]
Hi Alan. It's always good to hear from you.
I was careful to say throughout the article that graphing is my preferred method and that I learn more about the overall problem that way.
My agenda is larger than convenience when tweeting, of course. There are many types of equations where algebraic approaches are obviously quicker and more "accurate". But there are many more types (solving polynomial equations comes immediately to mind) where drawing a graph using a computer is much more efficient than using algebra - and gives (me) greater insights.
29 Oct 2013 at 1:43 am [Comment permalink]
I certainly didn't mean to appear critical of solving equations by graphing. It's what I prefer too 90% of the time - both for getting started by seeing what the problem "looks like", and for checking at the end to see that I haven't missed something (like extra solutions for example). And I agree that it's often all that we need - especially if we only want a rough idea of where the solution is.
I also am a fan of using software to zoom in on more and more accurate values (which is why I built that feature into my own "Graph Explorer" applet back in the last millennium). But after doing that I still like to point out that no matter how accurately we plot (and no matter how many zeros we get in the decimal representation of the answer), there is always that little extra "mystery" as to whether we really have it exactly.
29 Oct 2013 at 9:28 am [Comment permalink]
The iteration mathod is: x(1)=x(0)-y(0)/y'(0) where y' is the derivative of y in the point x(0)
If ln(x-3)=ln(x) - ln(3) then y=ln(((x-3)/x)+ln(3)
y'=3(x-3)/x
Starting with x=5 and several iterations:
y y' x1=x-y/y'
x= 5
0.1823 1.2000 4.8481
0.1342 1.1436 4.7307
0.0931 1.0975 4.6459
0.0609 1.0628 4.5886
0.0379 1.0386 4.5521
0.0226 1.0229 4.5300
0.0132 1.0132 4.5170
0.0075 1.0075 4.5096
0.0042 1.0042 4.5053
0.0024 1.0024 4.5030
0.0013 1.0013 4.5017
0.0007 1.0007 4.5009
0.0004 1.0004 4.5005
0.0002 1.0002 4.5003
0.0001 1.0001 4.5002
0.0001 1.0001 4.5001
0.0000 1.0000 4.5000
The solution is x=4.5 with the iteration method
31 Oct 2013 at 4:42 pm [Comment permalink]
@Miguel. Thanks for your addition. I suspect in this case simply doing "halving the interval" technique would get us there quicker?
19 Nov 2013 at 11:43 pm [Comment permalink]
Some comments.
Graphing is an additional tool. It is a completely different area of math. There is algebra, and there is geometry. And both involve different areas in our brain. You need both.
Maybe, we should not write 7(x-3), but 7*(x-3) or with a dot. This avoids confusion as if 7 is a function and all functions work like this.
I like your phrase "Since there are 2 log expressions with the same base that are equal to each other, we know the expressions in brackets must be equal". We could simply apply e^x on both sides, but then it is not clear, if the new equation is equivalent.
This makes me wonder, if you never use equivalence signs or phrases, but instead say "we have" or "solving gives"?
1 Dec 2013 at 4:15 pm [Comment permalink]
@Rene: I agree with 7*(x-3).
I wrote about the problems with the equal sign here:
The equal sign - more trouble than it's worth?
22 Jan 2014 at 2:01 am [Comment permalink]
My personal opinion is that the graphical solutions must follow the algebraic proofs! The reason for that is because we must teach students to be mathematicians, not problem solvers. A mathematician must be able to prove things, not only to find answers of concrete problems. When we show many graphical solutions to students, they tend to like them very much - yes, they are interactive, yes they are easy to understand, but yes... sadly they make the algebraic solutions to look "boring".
In the university where I work see that many times. Students who come from more prestige high schools (which have money to buy more computers, multimedia, interactive boards, etc) actually show much poor scores when they have to learn the theory of Linear Algebra than the others, who studied traditionally. And in the opposite - the students from the prestige schools was very fast problem solvers of problems in Analytic geometry; however it was hard for them to prove theorems.
Sadly I was teaching LA and AG for too short period of time and I was not able to do a serious research on that specific observation. What I wrote above was an assumption 🙂
22 Jan 2014 at 8:19 am [Comment permalink]
@Philip: Good to hear from you again.
The vast majority of people will not become mathematicians, but all will be problem solvers. Surely that's what we should help them do well?
22 Jan 2014 at 6:05 pm [Comment permalink]
While that's true for sure - most people will only use mathematics for regular problem solving; it's still the primarily target for the educational system to produce scientists (innovators), not just regular workers.
It's like in the football (soccer). There are many kids playing football on the street - most of the boys do. Not all of them go to the stadium to train in the kids training school. Only some of them go up to the youth team and few are selected to the mans team. And from all man teams, only few are at the level of Lionel Messy 🙂
Now imagine that the football clubs say "since majority of the kids will never be real good football players, why pushing them hard with learning strategies and tricks? For most of them it's good enough to play for fun only". Would you find a "Messy" that way?
It's actually different between countries. If you are a very big and rich country, say USA, you can afford to "buy scientists" from others. That way you can skip money and efforts from finding scientists, you can focus more pragmatically. On the other side - poor countries are forced to push hard towards finding scientists and innovators.
That's my (naive) explanation of why the rich countries are more like making "edutainment" instead of classic education 🙂