Hubble math

The Hubble Telescope [Source]

I came across this PowerPoint presentation about Hubble recently. The opening statement has a few errors. It says:

The Hubble Space Telescope is a robotic telescope located on the outer edge of the atmosphere, in circular orbit around the Earth at 593 km above sea level, with an orbital period between 96 and 97 minutes at a speed [of] 28,000 km/h. Named as a tribute to Edwin Hubble, [it] was launched into orbit on 24 April 1990 as a joint project of NASA and ESA, thus inaugurating the Great Observatories program. [The] cylindrically shaped Hubble weighs 11 tons. Its length is 13.2 m and its maximum diameter is 4.2 meters. The telescope can obtain images with optical resolution [finer than] 0.1 seconds of arc.

The first thing that struck me was the "circular orbit". All satellites, whether the moon around us, or the Earth around the sun, (or any satellite we have sent into space) orbits along an elliptical path. (An ellipse is a stretched circle.) This was discovered by Kepler in the 17th century and stated in his First Law of Planetary Motion:

The orbit of every planet is an ellipse with the sun at a focus.

To be fair, though, many orbits are very nearly circular. The amount of stretch of an ellipse is known as its eccentricity, [See more on ellipses.]

The following image clearly shows how low the orbit is. In fact, the Earth is "in the way" about half the time.

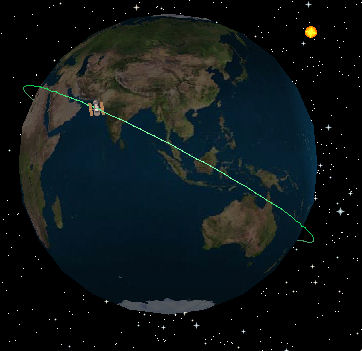
Low Earth Orbit [Image from the European Space Agency applet where you can see where the Hubble is right now.]

Weight of the Hubble

The Hubble does not weigh 11 tons right now. It is weightless. You only experience "weight" when you are being affected by gravity. While the Earth's gravity still acts on the Hubble, like all orbiting bodies it experiences "free fall", so is weightless.

More accurately, Hubble's mass is 11 tonnes. It would weigh about 108,000 N on the Earth.

Helix Nebula [Image source]

Optical resolution - seconds of arc

"The telescope can obtain images with optical resolution [greater than] 0.1 seconds of arc."

This is actually quite interesting. What does "0.1 seconds of arc" mean?

Angles are commonly measured in degrees. We know that a right angle is 90° and that a steep slope for a road is 15°. One complete revolution is 360°.

Here is a small angle (the smallest I can show without it looking like a single line), 2°, also called "2° of arc".

The Hubble Space Telescope needs to "see" very small parts of the sky. When we want smaller units than one degree, we take divisions of 1/60 of a degree, called minutes (just like 1/60th of an hour is one minute. Such divisions come from the ancient Babylonians).

If minutes are not small enough, we take 1/60th of a minute, to give us seconds (just like in units of time).

So "one second of arc" means 1/3600th of one degree.

But Hubble can do even better than that - it can discern a field of view which is 1/10 of 1/3600th, or 1/36,000th of one degree. Not bad!

The Radian

In science and engineering, the radian is a more convenient unit for measuring angles than the degree. One radian is the angle shown in this diagram. If we rotate around a circle such that we travel the distance of one radius, we will have traced out an angle of one radian at the center. It's about 57.3°.

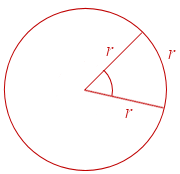
See more about radians.

So in radians, the Hubble can distinguish around 4.8 × 10^-7 of arc.

To finish, here's one of my favorite pictures by Hubble. It's a star that erupted in Jan 2002, and it was 600,000 times more luminous than our Sun.

[Image source: NASA]

Of course, the star erupted 20,000 years ago and it took that long for the light to reach us.

For more information on Hubble, see: http://asd.gsfc.nasa.gov/archive/hubble/

See the 6 Comments below.