IntMath Newsletter: XplorMath, Mathics, STEM challenge
By Murray Bourne, 22 Mar 2013
22 Mar 2013
In this Newsletter:
1. Math resource - 3D-XplorMath-J
2. Math resource - Mathics
3. National STEM Video Game Challenge - on now
4. ComputerBasedMath partners with Estonia
5. Math puzzle
6. IntMath Poll
7. Final thought: Passing civilization on
Welcome back to the IntMath Newsletter, after quite a long break. I've been very busy with several projects lately, but I hope to be able to find some time for writing again soon.
1. Math resource: 3D-XplorMath-J
3D-XplorMath-J is a delightful Java-based 3D math visualization program. It runs on Windows, Mac and Linux.
There is a large range of 3D and 2D objects that you can manipulate, explore and change parameters. You can create animations of 3D objects as they morph from simpler shapes, and there are even animations of ordinary differential equation solutions.
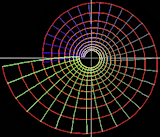
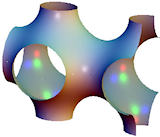
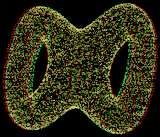

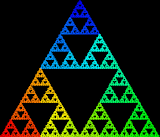

Unfortunately there is nowhere to enter your own functions, but even so, this is a valuable 3D visualization tool, kindly provided free by Richard Palais at University of Califormia Irvine.
Get your copy here: 3D-XplorMath-J
2. Math resource: Mathics
UPDATE: Unfortunately, Mathics seems to have disappeared.
A lot of math software is very expensive, but there are some good free alternatives.
Mathics is a "free, lightweight alternative to Mathematica". You can download it to run on your on own computer. (Unfortunately, the online version is rarely available.)
When you get there, click on the gallery link (at the bottom) to see some of the cool things Mathics can do (give it a few moments to process everything, and use a real browser like Chrome, Safari or Firefox.)
You can do your own math calculations with this tool - use the gallery as your starting point, or click the Documentation link at the top right of the screen.
3. National STEM Video Game Challenge - on now
The 2013 National STEM Video Game Challenge is accepting submissions right now. I think this is a great idea - learn some math and science while learning another valuable skill - game design.
From the site:
Game design is promising area of innovation in STEM learning. Research suggests that empowering youth to create their own video games promotes learner independence. Moreover, it encourages youth to take ownership over STEM knowledge, rather than viewing it as belonging to others, thereby ushering them into STEM communities of practice.
Entries will be accepted until April 24th.
It's a shame this challenge is only for the USA at this point. How about a worldwide challenge?
4. ComputerBasedMath partners with Estonia

Computerbasedmath.org is the brainchild of Conrad Wolfram, creator of Mathematica and Wolfram|Alpha. His view (which I largely agree with) is that we should change math education in the light of all the math software that is now available. We spend far too much time on theoretical algebra and not enough time using computer math tools to solve meaningful problems.
ComputerBasedMath recently announced they partnered with the first country ready for "this new kind of maths education": Estonia.
This collaborative project will address school statistics, using computer-based techniques to write a completely new and innovative curriculum. Focusing on equipping students with the skills and abilities needed for a twenty-first-century economy, the Minister of Education and Research in Estonia, Jaak Aaviksoo, states that now is the time for computer-based maths: "We believe in the enthusiasm and potential of the Internet generation--they are ready for computer based mathematics. It will also give them a competitive advantage in the labour market." [Source]
For more information on this movement, see the ComputerBasedMath FAQs.
5. Math puzzles
The puzzle in the last IntMath Newsletter was about Peter, the enthusiastic student who runs to school.
Correct answers with reasoning were given by Ibrahim, Peter Hunter, Thomas, Guido, Christopher and Nicos.
New puzzle: Professor Chng says he can represent the number one using (a) threes nines and a minus sign, and (b) one nine and two dots. How is that possible?
You can leave your responses here.
6. IntMath Poll
The recent IntMath Poll asked readers how important it is for them to know the historical background to the math they are learning.
Here is the result
Very important: 47%
Not important: 27%
Important: 25%
Total votes: 1800
It's obviously important for the majority of students that they know where the math comes from and why it was developed. This helps find meaning in what they learn.
New poll: The current poll asks readers about the method used by the teacher in class for delivering math questions. You can respond on any (internal) page of IntMath.
7. Final thought: Passing civilization on
This is from Lee Iacocca, Ford and Chrysler executive (b. 1924), and it speaks about the value of teachers:
In a completely rational society, the best of us would be teachers and the rest of us would have to settle for something less, because passing civilization along from one generation to the next ought to be the highest honor and the highest responsibility anyone could have.
Until next time, enjoy whatever you learn.
See the 8 Comments below.
22 Mar 2013 at 7:16 pm [Comment permalink]
a) (9/9)^9 (9/9 written as a fraction)
b) .9 recursive (.99999999999999999999999...)
22 Mar 2013 at 9:34 pm [Comment permalink]
9^(9-9) = 1
.9 reoccurring = 1
22 Mar 2013 at 9:56 pm [Comment permalink]
(a) 9-9 is zero and 9 to the power of this is 1 (i.e. 9^(9-9)=1)
(b) the decimal zero point nine recursive is equal to one (1-.9recursive = 0 therefore .9recursive = 1). This is mathematically written .9 with a dot above the nine, hence a nine and two dots.
23 Mar 2013 at 5:44 am [Comment permalink]
a) Three nines and a minus sign: 9^(9-9)
b) one nine and two dots: .9 and second dot over nine.
There are three symbols for recurring fractions: dash, dot (UK and USA) and () in Poland. So the solution is slightly tricky; it depends on nationality.
Regards
24 Mar 2013 at 3:53 am [Comment permalink]
New puzzle: Professor Chng says he can represent the number one using (a) threes nines and a minus sign, and (b) one nine and two dots. How is that possible?
Resp.: yes: 9^9-9. The power 0 of any number is 1
24 Mar 2013 at 8:27 pm [Comment permalink]
(1) 9^(9-9)
(better if I could write as superscript instead ^ sign)
(2) .9.
latter . is to say repeating decimal i.e 0.999... closer enough to 1
30 Mar 2013 at 5:22 pm [Comment permalink]
___9-9 0
1. 9 = 9 = 1
__ .
2. .9 = 0.9999… = 1
31 Mar 2013 at 3:14 am [Comment permalink]
Grey cells hurting,never-the-less;
(a)
Nine to the power of (nine minus nine) is equal to 1.
9^{9-9} = 9^{0} = 1
(b)
Point nine recurring represented with a dot over the 9 is a real number system representation of 1.
.\dot{9}