IntMath Newsletter: Cubes and cars
By Murray Bourne, 29 Oct 2015
29 Oct 2015
In this Newsletter:
1. Is cube root the same as raising to the power 1/3?
2. Resources: Mathematics in car research
3. Math puzzles
4. Math movies: Space Time
5. Final thought: Kindness
1. Is cube root the same as raising to power 1/3?
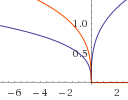 |
Is there a difference between cube root of a number, and raising the number to the power 1/3? Maybe there is! |
2. Resources: Mathematics in car research
a. Bloodhound Supersonic Car
The Bloodhound Supersonic Car is being developed by the UK in an attempt to break a new land speed record of just over 1600 km/h. Its pencil-shaped body will experience forces up to 12 tonnes per square metre (in the nose tip, which will be made using 3D printing), and up to 50,000 times the force of gravity (in the wheels, which will spin at over 10,000 rpm, or 174 rotations per second). The wheels will heat up to nearly 100°C during the attempt.
The main aim of the project is educational:
The BLOODHOUND engineering adventure provides us with a once in a lifetime opportunity to inspire the next generation of scientists and engineers. To achieve this ambitious goal, the BLOODHOUND Education Programme will be made available to all pupils in primary and secondary schools, and to students in further and higher education.
[Source: Bloodhound SSC]
Their Education section contains resources for secondary schools and Universities.
There are also related Math Questions.
b. Solar car race, Darwin to Adelaide
Now to an event that has more positive outcomes for our planet's future.
The World Solar Challenge 2015, held this month in central Australia, was won by Nuon Solar Team of the Netherlands.

Nuon Solar Car [Image source: Nuon Solar Team]
Teams from all over the world compete in a grueling 3,000 km five-day race, from Darwin to Adelaide.
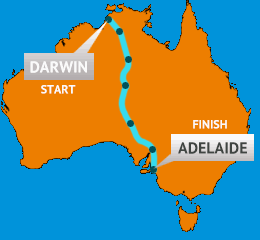
Route of solar car race [Image source: Nuon Solar Team]
The Nuon car averaged 91.75 km/h, which is similar to the speed conventional cars would achieve on this journey (considering driver fatigue).
Of course, these solar cars are light and not practical for daily commuting. What if there were hybrid solar cars that make use of the sun's energy while being parked outside all day?
Here is Ford's C-Max Solar Energi concept car that was released last year. It has solar panels on the roof, and a system for boosting the energy return from the sun.
Tom Murphy, associate professor of physics at the University of California, San Diego, has a detailed post on the mathematics behind solar-powered cars.
Schools should spend more time getting students to use their mathematics and science skills in solving the world's transport problems, especially as they relate to energy use and storage. These are certainly worthwhile concepts to inspire students about. Even if students don't end up in such research fields, hopefully it will improve their consumer behavior.
3. Math puzzles
The puzzle in the last IntMath Newsletter asked about circling 6 digits so their sum is 21. Most of the mathematical questions we come across (in text books, especially) have one correct answer, and we feel it's our job to hunt for it, then stop. But this was one of those puzzles where we need to think outside the box.
Plausible answers with explanation were given by:
a. Sachin, Don, Dennis, and Peter (who proposed 11+1+3+3+3 = 21)
b. Thomas and Lidia (who suggested turning the set of digits upside down, giving 6+6+6+1+1+1 = 21)
c. The "traditionalists" (who were certainly not incorrect) stated it was impossible, since an even number of digits when added can only give an even number. These were: George, Hammad, Dennis, Tomas, Argel, Mary, Arthur, and Henry.
So this is like a lot of real world problem-solving situations. There is often more than one interpretation of the "rules", giving more than one plausible solution.
New math puzzle
What is the maximum number of times 2 will divide into 50! exactly?
You can leave your responses here.
4. Math movies: Space Time
Here are two videos from the PBS Space Time series. These will certainly challenge some of your ideas about how gravity and curves work!
Is Gravity an Illusion?
 |
This video is a mind-bender. It's fast-paced, and there's a lot to think about. Feel free to watch it more than once! |
Can a Circle Be a Straight Line?
 |
This follow-up video is more mathematical, and examines the concept that curved lines can really be thought of as a series of straight parts, which is an important concept in calculus. See: |
There are more videos in this series. You'll see links to them in YouTube.
5. Final thought: Kindness
The 16th century Spanish novelist, part-time tax collector and accountant Cervantes wrote the following. It's as relevant today as it was in his time.
Great people create great acts of kindness. [Miguel de Cervantes, 1547-1616]
Until next time, enjoy whatever you learn.
See the 16 Comments below.


29 Oct 2015 at 6:02 pm [Comment permalink]
The answer to this weeks puzzle is 25...I think?? 25 2's form 50.
29 Oct 2015 at 8:54 pm [Comment permalink]
Hello Murrey, " Can a circle be a straight line"?
First thought that came into my head without going to the video link was of course Yes!
Thousands of aircraft routinely fly great circle routes every day around the world, that being the shortest distance between two points and therefore one assumes a straight line.
As always thanks for your always thought provoking Newsletter content, mostly way above my mathematical knowledge, but always interesting.
Kind regards, Roger
29 Oct 2015 at 11:03 pm [Comment permalink]
25!
29 Oct 2015 at 11:09 pm [Comment permalink]
29333495129
30 Oct 2015 at 6:25 am [Comment permalink]
47
2 1
4 2
6 1
8 3
10 1
12 2
14 1
16 4
18 1
20 2
22 1
24 3
26 1
28 2
30 1
32 5
34 1
36 2
38 1
40 3
42 1
44 2
46 1
48 4
50 1
1 + 2 + 1 + 3 + 1 + 2 + 1 + 4 + 1 + 2 + 1 + 3 + 1 + 2 + 1 + 5 + 1 + 2 + 1 + 3 + 1 + 2 + 1 + 4 + 1 = 47
30 Oct 2015 at 8:07 am [Comment permalink]
ANSWER = 47
USED 10 LINES OF QUICKBASIC
CONSIDER EVEN INTERGERS 50 TO 2
LET N BE ONE OF THE EVEN NUMBERS
SET NO=N
TEST: NO/2-INT(NO/2), IF 0 THEN
COUNT =COUNT +1
RESET NO, NO=NO/2
REPEAT TEST
SUM COUNT OVER ALL VALUES OF n
ans =47
30 Oct 2015 at 9:43 am [Comment permalink]
There are 25 even numbers. That starts us off with 25 "2" factors.
There are 12 numbers evenly divisible by 4. That gives us another 12 "2s". Each already had given us one factor, this just adds another.
There are 6 numbers evenly divisible by 8 for another 8 "2s". There are 3 numbers evenly divisible by 16 and, finally, one number evenly divisible by 32 which contribute 4 more 2s.
25 + 12 + 6 + 4 = 47 times we can evenly divide 50! by 2.
30 Oct 2015 at 10:16 am [Comment permalink]
I use Mathematica's function FactorInteger which yields
FactorInteger[50!] = {2^47, 3^22, 5^12, 7^8, 11^4, 13^3, 17^2, 19^2, 23^2, 29^1, 31^1, 37^1, 41^1, 43^1, 47^1}
as the decomposition of 50! into prime factors (in less than 0.0001 seconds). Then 47 is the maximum number of times 2 will divide into 50! exactly.
50!/2^47 = 216105129892080882169214875191192738017616943359375
30 Oct 2015 at 11:43 am [Comment permalink]
The maximum number of times 2 can divide 50 is once
1 Nov 2015 at 7:53 am [Comment permalink]
2 will divide 50!
15 207 046 600 856 689 021 806 304 083 032 384 422 188 820 784 480 256 000 000 000 000
times
1 Nov 2015 at 8:12 am [Comment permalink]
This is my first time of coming to this site, and I found it very useful to those who want to incline in Mathematics. Thanks to intmath
5 Nov 2015 at 6:36 am [Comment permalink]
Answer: 25+12+6+3+1=47
Explination:
You multiply all the natural numbers from 1 to 50. Of these 25 are even, so you can devide 25 by 2. (25)
The answers are then the numbers 1 to 25. Of these 12 devide by 2 and give 1 t0 12. (25+12)
Of the numbers 1 to 12, 6 are devisable by 2 (25+12+6) and gives the numbers 1 to 6 as answers.
Again 3 of these are devisible by 2 (25+12+6+3) and gives answers 1, 2 and 3 of which just a single one is even and the answer is not even again. Thus we get 25+12+6+3+1=47
5 Nov 2015 at 9:37 am [Comment permalink]
If you mean only this one '2', then we obtain '1'(meaning 'once') for the answer.
However, if you mean 'keep dividing 2 into the given number' then we need to solve: 2^x = 50! which gives us 214 times.
17 Nov 2015 at 9:55 am [Comment permalink]
Once only
26 Nov 2015 at 8:48 am [Comment permalink]
The results for the puzzle in this Newsletter can be found here: IntMath Newsletter 26 Nov 2015
28 Nov 2015 at 3:22 am [Comment permalink]
2*2*2*2*2*2*2-(2*2*2*2)-(2*2*2)-(2*2)/2=50
the correct answer is 17
KARIM AZMY