IntMath Newsletter: Rankbrain, Wallis, log-log and scalars
By Murray Bourne, 26 Nov 2015
26 Nov 2015
In this Newsletter:
1. Math in the news
2. Resource: Semilog and log-log page
3. Is a 1x1 matrix a scalar?
4. Math puzzles
5. Math movies: Comics that ask "what if?"
6. Final thought: Just do it!
1. Math in the news
a. Google Rankbrain
Google has been remarkably successful as a search engine due to its uncanny ability to (mostly) find the exact page we need in response to the questions we throw at it.
But that's because we ask similar questions most of the time, and those questions are fairly unambiguous (like "weather New York", or "formula for area of circle", or perhaps "flights to London".)
However, around 15% of all Google queries are novel (no-one has asked it before) and/or may require natural language interpretation (for example the question, "What time does it get dark in the Philippines?" requires an understanding of the term "get dark"). This has proved quite a challenge for Google (and its competitors), but like the rest of their approach, math has come to the rescue.
Google's Rankbrain is a new vector-based artificial intelligence approach to the problem of what natural language searches could mean. These "word vectors" are basically the result of assigning numbers to possible meanings of words. If the vectors line up sufficiently well, then that's probably what the query really means.
According to Google’s Chief Executive Officer Sundar Pichai:
“Machine learning is a core transformative way by which we are rethinking everything we are doing.”
There could be some job opportunities in this going forward. (Google has hired many aritifical intelligence scientists over the last few years.)
For more details:
Google Turning Its Lucrative Web Search Over to AI Machines (by Bloomberg)
"Thought vectors" could revolutionize artificial intelligence (by ExtremeTech)
b. Wallis, pi and quantum theory
Seventeenth century English mathematician John Wallis developed an approximation for π involving the product of simple fractions. His result was recently proved in a novel way involving quantum theory.
Wallis contributed quite a few other mathematical insights, some of which I outline in this article.
 |
A quite remarkable new proof of the 400 year-old Wallis Product approximation for π has recently been published. It arises from a study of the quantum mechanics of the hydrogen atom. |
2. Resource: Semi-log and log-log Graphs
I find a lot of people don't readily grasp the concept of semi-log or log-log graphs, so when they come across a statistical graph containing such axes, they complain it is "misleading" (They are used to the axes always having equally-space gaps.)
 |
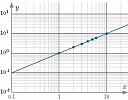I recently updated the IntMath page on semi-log and log-log axes. The page concludes with an interesting real-life case of log-log graphs, the Zipf Distribution. |
3. Is a 1×1 matrix a scalar?
 |
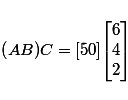A 1x1 matrix is often regarded as a scalar quantity, but is that correct? This article explores a reader's question. |
4. Math puzzles
The puzzle in the last IntMath Newsletter asked about division of a factorial number.
Correct answers with explanation were given by: Don and Tomas (who both used a software approach), and Francis, Salomon and Γιώργος Βαρελάς (Giorgos Varelas) (who enumerated all possible cases).
There were a few "traps" for the unwary in that puzzle, including the "factorial" sign (!) which some people missed altogether (understandable, sine it's not good math notation), and the "divide into" terminology.
For those who are still not sure what's going on, here's a simpler example: The number 5! can be divided evenly by 2 three times, since there are three 2's in the prime factorisation of 5!:
5! = 120 = 2 × 2 × 2 × 3 × 5
New math puzzle
An ant on a sheet of coordinate paper starts at the point (3,4), proceeds
by a straight line path to the nearest point on the unit circle, and then
follows the arc of the circle to the point (1,0). How far did the ant walk? (Units are cm.)
You can leave your responses here.
5. Math movie: Randall Munroe: Comics that ask "what if?"
I've been a XKCD comics fan for some time since his simple stick figure cartoons are often thought-provoking and are often math-related. His tagline is:
A webcomic of romance, sarcasm, math, and language
(Some of the topics discussed may not be suitable for all ages. Make your own determination.)
He gets a lot of crazy questions from readers which he addresses in the What if? section.
Here's his TED talk about some of those questions, and his responses.
 |
Web cartoonist Randall Munroe answers simple what-if questions ("what if you hit a baseball moving at the speed of light?") using math, physics, logic and deadpan humor. |
6. Final thought: Just do it!
Today's quote comes from Butch Lovelace. It's for those of you who struggle to get going some days:
The most difficult thing is to just start the ball rolling. Once it starts, it's actually more difficult to stop it. [Butch Lovelace]
Until next time, enjoy whatever you learn.
See the 16 Comments below.
26 Nov 2015 at 5:51 pm [Comment permalink]
What a great question. I'm giving it to my 6th Form next lesson. When I just solved it, the key was working out where the nearest point was. Like most maths, a good diagram pays dividends π
26 Nov 2015 at 7:02 pm [Comment permalink]
@Tim: Great! How did your lesson go?
26 Nov 2015 at 9:45 pm [Comment permalink]
The answer is 5.4142135
26 Nov 2015 at 10:58 pm [Comment permalink]
Hi Murray
first time I try one of your puzzles. Don't know if you remember, but you helped me to get mathematics on the net:). Here is my solution:
Point on circle:
and 
Distance from (3;4) to point on circle squared:
=
Differentiate and = 0:
Thus
Distance between this point and (3;4) = 4 (shortest distance to circle)
Distance between this point and (1;0) squared
=
Use cosine rule to obtain angle at (0;0):
Length of arc = the same.
Thus total distance = 4.927295218
This can all be done in GeoGebra as well.
26 Nov 2015 at 11:18 pm [Comment permalink]
4+(pi/4) cm
Straight line distance was 4cm. Arc distance was (pi/4)cm.
27 Nov 2015 at 12:19 am [Comment permalink]
1. The line segment joining the origin O to the point p = (3, 4) has length 5. This segment intersects the unit circle at the point nearest to p. Call q the point of intersection.
2. So the (shortest) distance from the unit circle to p is equal to 4 (= 5 - 1, the radius of the unit circle).
3. The length of an arc along the unit circle is equal to the angle it subtends (in radians). The angle a formed by the horizontal axis and the line Op is found by solving ArcTan(a) = 4/3, which gives a = 0.927.
4. So, the ant walks 4 (length of the distance from p to the unit circle) plus 0.927 (length of the arc from (1, 0) to the intersection point q -which lies on the unit circle at an angle a from (1,0). I.e.,the total length of the walk is 4.927 cm.
27 Nov 2015 at 1:24 am [Comment permalink]
Hii my answer for the ant puzzle:
First of all the ant walks on the straight line AB (y=4/3 X) that its length is equivalent to a
We can simply calculate "a" because A(3,4) and B is the intersection of the line AB : Y=4/3 X and the circle : X^2 + Y^2 =1 which gives us x=3/5 and y=4/5
(X here has 2 values + and - but we are in the right so the answer is the positive one)
Therefore a=4 (image also includes calculations)
We need now to calculate the arc length to (1,0) and we find out that there are two ways to go to the point (1,0) either from right walking on the arc or left on the arc which will lead to the same point (1,0)
If it goes right we need to find length b (in the image it is the arc length from the point B to (1,0) )
b= (arc angle)/360 Γ(2)Γ(radius)x(Ο)
Then b=0.9273
And the distance that the ant walked is
a+b=4.9273
If it goes left we need to find length c
(The opposite direction)
Applying the same formula
C=5.355892
And the distance that the ant walked is
a+c=9.355892
27 Nov 2015 at 3:43 am [Comment permalink]
distance travel is 4+(6.28)*(53.1)/360
4.4636
27 Nov 2015 at 9:00 am [Comment permalink]
βMachine learning is a core transformative way by which we are rethinking everything we are doing.β
This stuck a chord with me. I am interested in Phenomenology which is about thought process and how the intellect handles perceived empirical data to coordinate instinct, memory, imagination, intuition, daydreams, and poetry, etc. The Rankbrain is kind of a mathematical approach to perceptual psychology and naming conventions. This is very exciting. Thank you.
27 Nov 2015 at 8:46 pm [Comment permalink]
Greetings to all readers. The ant walked 4.92729 cm, because;
Start to centre = SqRoot(3 squared + 4 squared) = 5
For unit radius circle, Start to nearest point on circle = 5 - 1 = 4 cm
Tan of angle to X axis = 4/3
The angle having this Tan is 0.92729 Radians
For unit circle this = distance travelled along arc in cm
Total distance travelled by ant = 4 + 0.92729 = 4. 92729 cm
27 Nov 2015 at 11:01 pm [Comment permalink]
Dear sir,
The answer is 4.9273cm approximately.
Explanation:
The ant has reached point (0.6,0.8) from (3,4) and then if it has traveled in clocked direction..
Straight path of 4 cm and arc of 0.9273cm. Totally. 4.9273cm
The articles you are sharing in the newsletter are very encouraging sir.. Thank you..
28 Nov 2015 at 2:00 am [Comment permalink]
Kindly refer to " 4 Math puzzles ". I am aged 76 and what I remember with reference my college studies which ended in March 1959 after which I had nothing to do with Mathematics is that Factorial 5 is 5x4x3x2x1= 120 Factorial 10 is 10x9x8x7x6x5x4x3x2x1 = 3628800
1 Dec 2015 at 1:35 am [Comment permalink]
I hope this is the right place to post proposed solution to this month's problem ...
Re distance ant travels from point (3,4) to unit circle then to x-axis along circle's perimeter ...
Solution 1:
The points (3,0), (3,4), and (0,0) form a 3-4-5 right triangle. This triangle is similar to the right triangle formed
by (x,0), (x,y), and (0,0), where (x,y) is the point in which the line y = (4,3)x intercepts the unit circle ... By direct proportion (x,y) is the point (3/5, 4/5) ...
The hypotenuse of the smaller triangle is one; of the larger one, 5: so the distance from point (3,4) to the unit circle is four.
The magnitude of the arc length on the unit circle is s = radius x theta, where theta is the central angle of the circle ... In this case s = 1 x theta ... Now tan theta = 4/3, since it's the slope of the line y = (4/3)x ... So, theta is arctan 4/3 ...
So total distance traveled by the ant is: 4 + arctan 4/3 ...
Solution 2:
If you don't recognize the 3-4-5 triangle you can solve for the point of the line y = (4/3) and the unit circle
by substituting y^2 = ((4/3)x)^2 into x^ + y^ = 1 ...
3 Dec 2015 at 5:53 am [Comment permalink]
answer to walking ant puzzle:
Min. distance from 3,4 to Unit circle of radius 1.0 cm
equals 4.108 cm. Location on circle @ +66.425 degrees at
X = 0.375 and Y = + 0.8594
Arc distance walked 23.575/360 * 2* PI * R where R = 1 cm &
Arc distance =0.412 cm.
Total distance the ant walked is 4.52 cm.
7 Dec 2015 at 6:48 am [Comment permalink]
Ant's journey is divided in two steps: 1)from P1(3,4) to the "nearest" unit circle's point P2 and 2)the arc P2 to P3(1,0).
The nearest circle's point is P2, where the line y=4/3*x intersects the unit circle y^2+x^2=1. This point is P2(3/5,4/5). The distance P1 - P2=d is given from the Pythagorian Theorem:d^2=(4-4/5)^2+(3-3/5)^2 => d= 4cm.
The angle "a" between axis x and y=4/3*x is given by sin(a)=4/5. The arc matches to that angle is 2*pi/5=1.256cm.
The total distance travelled is d+2*pi/5=4+1.256= 5.256cm
15 Dec 2015 at 2:04 pm [Comment permalink]
second try
4.926046 cm
approch (I call it brute force)
loop on x, compute y=sqr(1-x^2), d=sqr(4-y)^2 +(3-x)^2)
find smallest d =d(min) save x0 and yo, d(min)=4cm
ant strikes perpendicular to unit circle thus eq of linear path
has zero y intercept.(remembered from Calculus of Variation) I used this to check my y0 , ATN(y0/x0) radians =.926046. Since
unit circle total distance is
4 +.926046 cm
GREAT PROBLEM THANKS, don