A Rare Fibonacci Day
By Casey Allen, 13 Aug 2021

Today is rather special. A day like today won't come around for almost another century. Today is rare and represents a “golden” opportunity for those in the know.
Have you guessed it?? Well since you clicked on the title you already know the spoiler...
Today, 8-13-21, combines three adjacent numbers in the Fibonacci Sequence. The mathematically progressing sequence obtained by starting with 1 and 1, and then successively summing the prior two numbers to get the next one.
Example:
1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, and so forth...
Fibonacci Sequence:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…
The last time we landed on a rare fibonacci sequence was 5-8-13, and as you can see from the full sequence the previous occurrence was even further back.
Mathematics can be found everywhere and Fibonacci numbers are especially prolific. Let's explore its occurrences and applications.
Nature

Photo credit: Esdras Calderan/wikipedia (CC BY 2.0)
We see them in nature – in the spirals of pineapples, sunflowers, succulents, and pinecones. Look closely enough and you'll be able to see Fibonacci at work everywhere.
Finance
Image by Sabrina Jiang © Investopedia 2020
Day traders have been using fibonacci retracements to hopefully predict inflection points in the markets. Traders will often use these tools in combination with other trading algorithms to identify potential buying opportunities and conversely signals to either sell a position or take a short position on a particular equity.
Architecture
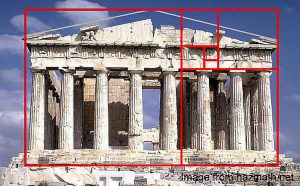
The Parthenon, probably the most well known structure to use the golden ratio. The ancient greeks were known for their admiration of the mathematical constant. However, they weren't the first to apply its principles to architecture. It's believe that the Egyptians applied the ratio when building the great pyramids.
Art

In the same vein as architecture, master painters have been using the golden ratio as the basis of composition that draw a viewer's eyes into key areas of a painting, imparting a sense of emotion and story.
Mathematically, the Fibonacci numbers have many more applications and natural occurrences. Most of which are still being discovered and proven out. For example, by proving out Zeckendorf's Theorem you could represent all integers as Fibonacci numbers.
Compounding also applies to Fibonacci numbers, as can be seen in the Fibonacci sequence itself. The sequence's growth is exponential and infinite, which leads us back to why today is so rare! Due to the nature of the sequence, days like today were more numerous and closer together at the start of the century, but get scarcer and farther apart as time passes.
Sadly, we won’t see another Fibonacci day for another 81 years in 2102.
So take advantage of today and enjoy the beauty of Fibonacci all around you in nature, architecture, beauty, and art.
See the 1 Comment below.
20 Sep 2021 at 5:01 am [Comment permalink]
[…] The SquareCirclez blog explores the beauty of the Fibonacci Sequence in A Rare Fibonacci Day. […]