Is Phi a Fibonacci furphy?

The science show Catalyst recently ran a piece debunking the Phi myth.

The reporter (Dr Paul Willis) sets out to demonstrate that the so-called "natural appearances" of the Golden Ratio, Phi, is an urban myth.

The ratio Φ (the Greek letter Phi) can be obtained by taking a term of the Fibonacci Sequence and dividing it by the term before.

The sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...

For example, 89/55 = 1. 618181818... Taking higher terms gives a value closer and closer to Phi = (1 + √5)/2 = 1. 618033989...

Myth #1

In the da Vinci Code, Dan Brown claims these mathematical curiosities can be found in the nautilus shell. It’s found by measuring from the centre to the outer radius and dividing that by the distance from the centre to the inner radius.

They measure a nautilus shell’s inner and outer ratios and find that the ratio is close to 3, not 1.618.

Strike 1.

Myth #2

Let’s have a look at the most famous claim about Phi appearing in nature is a person’s height divided by the distance from the naval to the floor 1.618?

At this point, they proceeded to (very roughly) measure a female model’s height and distance from the floor to the navel. The ratio was close (1.592), but not Phi.

But wait a minute. Leonardo daVinci’s famous Vitruvian Man is an idealised figure (in the tradition of the Greeks, who drew and sculpted "perfect" people based on certain ratios).

In the following Vitruvian Man drawing, the navel is at the dead center of the body and the extremities of the legs lie on a circle. When the arms are drawn outstretched, the extremities of the hands are on the circle. The ratio of the total height to the height of the navel is (very close to) 1.618.

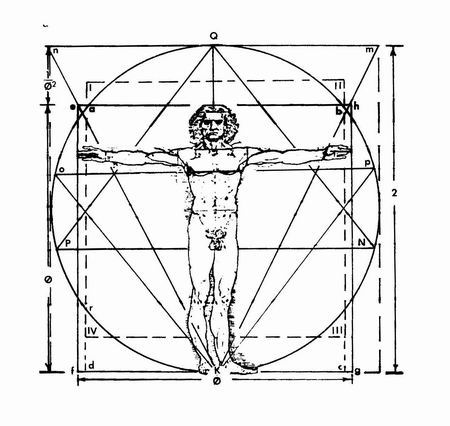
So while us mere mortals do not have such perfectly proportioned bodies, I’m not sure it completely debunks Phi.

Myth #3

... Let’s try the insect world. According to Fibonuts the ratio of female to male to male bees should be Phi, 1.618.

Once again, urban legend has got in the way of Phi. The real story with bees:

A female bee has both a female and a male parent, but a male bee has only a female parent, so if you count up the number of parents and grandparents of each generation, you get a fib number.

So I don’t really regard this as debunking the natural occurrence of Phi when it comes to bees. Willis was listening to the wrong story.

[Fibonacci first developed his sequence after considering how many rabbits there would be in a field if they never died, they mated once a month, they had one male and one female offspring each month, and all their offspring mated with each other.]

Myth #4

Now we turn to sunflowers.

The obvious thing your eye catches are these spirals going out like that, and if you count the number of spirals going clockwise, that will be a Fibonacci number, and if you count the spirals going counterclockwise, it will be an adjacent fib number.

This one is true.

Willis’ conclusion?

So, Phi is not found in the spirals of a nautilus shell nor the proportions of the human body, but the Fibonacci sequence reveals itself in the ancestry of bees and the head of a sunflower. But, that’s still a strike rate of fifty/fifty, not bad for an urban myth really.

My conclusion?

Actually, I thought this was pretty bad television. Many of Catalyst’s stories are very interesting, but every so often they do a pseudo-scientific piece, complete with ’smarmy’ tone, like this current ’study’ on Phi.

I think it was supposed to be anti-Dan Brown. But if any students were watching it, they would have walked away being cynical about their math teacher’s attempts to make mathematics interesting using Golden Ratio.

You may be interested in Math of Beauty, where you can check the mathematical beauty (or otherwise) of several famous people using a Phi-based mask.

Update: Carver, from the Philippines used Photoshop to re-organise his own face using the Math of Beauty mask.

See the 7 Comments below.