IntMath Newsletter: Piano trig applet, continued fractions
By Murray Bourne, 31 Jul 2017
31 Jul 2017
In this Newsletter:
1. New applet: Piano note frequencies interactive
2. Resource: Continued fractions
3. Math in the news: Space filling
4. Math movie: One in a million
5. Math puzzle: clock
6. Final thought: Really worth the doing
1. Frequencies of notes on a piano - interactive learning object
 |
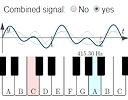Explore piano note frequencies in this new interactive learning object, combining trig graphs and exponential growth. |
Here's some background on what's going on:
What are the frequencies of music notes?
Frequency of notes on a piano - interactive learning object
2. Resource: Continued Fractions
You may recall the Euclidean Algorithm for finding the greatest common divisior of 2 numbers. For example, the GCD of 93 and 42 would be found as follows:
93 = 2 × 42 + 9
42 = 4 × 9 + 6
9 = 1 × 6 + 3
6 = 2 × 3 + 0
We stop at that last line because there is a remainder of 0, and we conclude the GCD is 3.
Continued fractions are a special form of fraction and can be used when finding GCDs, as well as in many other applications like finding square roots and solving quadratic equations.
 |
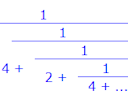This extensive resource covers continued fractions. It contains many worked examples and several online calculators and it's by Richard Knott, Surrey University: |
3. Math in the news: Space filling
Fruit shop owners know a thing or two about space filling. They need to display their wares attractively, safely and in a space-efficient way.
Mathematicians have studied space filling for some years, especially since
Lord Kelvin (the temperature guy) asked in 1887:
How can space be partitioned into 3D structures of equal volume in a way that minimizes the total surface area of each structure?
Some Belgian mathematicians had some breakthroughs on this issue last year. From Phys.org:
 |
Researchers in 2016 discovered a new 3D structure that divides space into 24 regions, and have shown that it is the best solution yet to a modified version of a geometrical space-partitioning problem that has challenged researchers for more than a century. See more: |
4. Math movie: How to visualize one part per million
A lot of people struggle with very large (or very small numbers). It's not surprising as most of us don't use them every day, but as we do hear about them constantly on the news, it's important to get a good conception of them.
 |
In this short TED-Ed video we get some good pointers on what one million really looks like.
How to visualize one part per million
|
5. Math puzzles
The puzzle in the last IntMath Newsletter asked how far a person walked given some (seemingly) insufficient conditions.
Correct answers with explanation were provided by Chris, Thomas and Nash.
The walking problem was based on one by Lewis Carroll, author of Alice in Wonderland, and Through the Looking Glass. It appeared in his book A Tangled Tale. Apart from being a well-known author, Carroll (real name Charles Lutwidge Dodgson) was a mathematician, logician, Anglican deacon, and photographer.
New math puzzle: Clock
True or false? Consider a clock at 11:40 AM. When the second hand reaches somewhere close to 20 seconds past the minute, the clock face will be divided into 3 equal parts. How about for any other cases (like close to 01:45:30, or 02:50:35)? Is it true? Can you prove your conclusion for the clock at any time?
You can leave your responses here.
6. Final thought: Really worth the doing
Today's quote is from Lewis Carroll:
One of the secrets of life is that all that is really worth the doing is what we do for others.
Until next time, enjoy whatever you learn.
See the 7 Comments below.
1 Aug 2017 at 12:36 am [Comment permalink]
False.
An equal 3 part division for the hands of the clock would be 120 degrees (360/3). The hour hand at 4 and 8 would have the minute hand pointing at 12. However, the second hand must also be at 12 at those times. There is no perfect integral or congruence given the ratio with the 3 hands of a clock to form an equal 3 part division.
Rick
4 Aug 2017 at 2:49 pm [Comment permalink]
None of those times equally divide the clock face. The angles can be calculated as follows:
At 11:40:20 the H:m angle = 1.89, H:s = 2.27, m:s = 2.13
Closest I could get was 11:38:18 which gives areas: H:m = 0.332, H:s = 0.330, m:s = 0.338
5 Aug 2017 at 11:51 am [Comment permalink]
Let's assume the noon direction is angle 0, with positive angles in the clockwise direction. Let's also assume that all numbers are modulo 360.
We can find out the angle of each clock dial.
SecondsAngle = 360*seconds/60
MinutesAngle = 360*(minutes/60 +seconds/(60*60))
HoursAngle = 360*(hours/12 + minutes /(60*60) + seconds/(60*60*60)
It doesn't matter which is which, but rank the angles of the dials.
If smallestAngle+120=SecondSmallestAngle
And SecondSmallestAngle+120=LargestAngle
Then the watch face is split equally into three parts.
5 Aug 2017 at 5:37 pm [Comment permalink]
Bruted it out in VBA and found the very closest times at which the three segments are closest to 1/3 of the face:
6:10:51 and 5:49:09
7 Aug 2017 at 4:04 pm [Comment permalink]
Consider the clock face divided into 12*3600 units. The time on our clock is 7 55 00 ; minute hand on 11 and
Hr hand is just shy of 8; 7 plus (55/60) . In our units,
Minute. - -- 11* 3600 =. 39600, and
Hour. ..... 7* 3600 + (55/60)*3600 = 28,500
Subtracting. 39600 - 28,500. = 11,100
This leaves 32100 for two remaining sectors.---16050 each. NOT evenly divided.
If the clock advances to 8 even, this difference is 43200 - 28800 = 14400 ( 4 hours) dividing the remaining 28800 by two puts the second hand at 4 yielding 3 near equal sectors.
(Note: Near equal sectors also occur if the hour hand is on 4 and minute hand on 12
All cases where the minute hand is NOT on 12 yield larger errors (differences from 120 deg)
9 Aug 2017 at 8:39 am [Comment permalink]
Hours angle = Hours*30 + Mins/2 + Secs/120 Degrees
Mins angle = Mins*6 + Secs/10 degrees
Secs angle = Secs *6
Explained:-
Routine to determine if for given time the Hour, Minute and
Second hands are at 120 degrees to each other.
For analogue clock, ie mins and secs NOT impulse stepped.
If given time in 24 hour format, convert to 12 hour format.
If the hours in given time is 12 change to 0.
Angles are clockwise from the 12 o'clock position = 0 to 365 degrees.
For SECONDS hand, each second it travels 360/60 = 6 degrees;
so angle of Seconds hand on clock face
= (given time in Secs)*6 degrees
= Secs *6 ..........................(1) Secs
( Seconds can be given with decimals for more precise positioning as
0.5 secs travels 3 degrees, and 0.1 sec travels 6/10 = 0.6 degrees.)
For MINUTES hand, each minute it travels 360/60 = 6 degrees;
so angle of Minutes hand on clock face
= (given time in Minutes)*6 degrees + the minute portion of the Seconds hand.
= {Given Mins + (Given Secs/60)} *6 degrees
= Mins*6 + Secs/10 degrees.....................(2) Mins
For the HOUR hand, each hour it travels 360/12 = 30 degrees.
But allowing for the portion of an hour the Minutes and Seconds hands
move on the Hour hand from it's on the exact
say 6,7 or 8 o'clock marked positions:
The angle of the HOURS hand on the clock face is,
= (Given time in hours + Given Mins/60 + Given Secs/3600)*30 degrees
= Hours*30 + Mins/2 + Secs/120 Degrees. . . ................(3) Hours
Only if the 3 angles returned by Equations (1), (2), and (3) are 120 degrees
apart then the given time meets the requirement. Tolerence? Say about +/- 1 degree.
Example; For time 8:22:2 using Eqs (3), (2) and (1) respectively yields angles;
251.02, 132.2 and 12 degrees, which are +/_ 1 deg of being 120 deg apart.
Time 12:20:40 has angles, 10.33, 124, 240, what looked good is > 10 deg off.
Reminder for this calculation the 12 must be changed to 0.
Your examples:11:40:20 has angles 350,242 and 120, off by 10 degrees.
Your time 2:50:35 has angles 85, 303, 210, off by 20 deg.
12 Aug 2017 at 10:04 am [Comment permalink]
One can proceed visually by drawing a clock face with the three hands positioned at 120 degrees distance from each other and rotating this configuration about its center to find admissible time positions. Note that the minute hand can be located before or after the hour hand. What I did (using Mathematica) is to find the positions where the percent circular distance of the hour hand between each hour marking and the next is equal to the percent circular distance of the minute hand between 12 pm and any given position. This method gives more or less precise times on the clock face. There 22 in all (since there are two positions, 4:00 and 8:00, where there is a coincidence). The 22 approximate admissible positions are 1:26, 1:49, 2:32, 2:54, 3:58, 4:00, 4:43, 5:05, 5:49, 6:11, 6:54, 7:16, 8:00, 8:21, 9:05, 9:27, 10:11, 10:32, 11:16, 11:38, 12:21,12:43