What are the frequencies of music notes?
In the table of frequencies below, you'll find A = 440 Hz, and then
A# = 466.16 Hz,
B = 493.88 Hz,
C = 523.25 Hz, etc.
Also, you can find Middle C: 261.63 Hz.
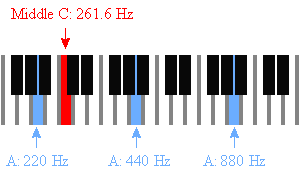
Table of Musical Frequencies
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequency
130.82
138.59
146.83
155.56
164.81
174.61
185
196
207.65
220
233.08
246.94
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequency
261.63
277.18
293.66
311.13
329.63
349.23
369.99
392
415.3
440
466.16
493.88
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequency
523.25
554.37
587.33
622.25
659.26
698.46
739.99
783.99
830.61
880
932.33
987.77
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
C
Frequency
1046.5
1108.73
1174.66
1244.51
1318.51
1396.91
1479.98
1567.98
1661.22
1760
1864.66
1975.53
2093.00
These are found using
frequency `= 440×2^(n"/"12)`
for `n = -21, -19, ..., 27`
Where did this formula come from?
This problem reminded me of Compound Interest that we met earlier in Money Math. The frequency needs to double every `12` notes (because there are `7` white notes and `5` black notes in each octave.)
Here is a graph of that relationship:
frequency `= 440×2^(n"/"12)`
This is an exponential curve, that we met earlier in Graphs of Exponential Functions.
Equal Tempered Tuning
An interesting problem has faced musical instrument makers for hundreds of years. To get a "perfect 5th" (the interval between A and the E above, say), we need to play a note which has `1.5` times the frequency of A.
On a violin (or viola or any fretless stringed instrument) this is possible, and we can play a beautiful, perfect E at `440 × 1.5 = 660\ "Hz"`. But notice (from the frequency table above) that a piano playing the same note will play E `= 659.26\ "Hz"` [just a little flat!].
Around 400 years ago, keyboards (usually harpsichords and organs) were tuned for a particular group of keys, so that all the instruments, especially strings, sounded "right" in those keys. The harpsichord sounded great in those keys, but pretty awful in other unrelated keys (say B flat).
There were actually several different tuning systems in use during Bach's time, including meantone (which aimed to make major 3rds sound good, but was not as concerned about the quality of major 5ths, with the effect that some keys were not usable), and Werckmeister's 1691 tuning which allowed composers to create music in any key (with the effect that the various keys had a different tonal quality).
In the early 20th century, it was decided to tune keyboards so that the notes were evenly spaced (like the frequencies given in the table presented above). This is called equal tempered tuning. Such tuning was known in the time of Bach, but rejected because it was regarded as too "bland" (all keys have the same tone quality) and there were no frequency measuring tools that would have allowed exact tunings.
Unfortunately, equal tempered tuning means all stringed instruments have to allow for the slight differences in tunings between instruments when keyboards are also involved. Strings are usually happiest when playing with other strings only, for this reason.