IntMath Newsletter: Pollution, trig ratios and infinity

4 Jul 2013

In this Newsletter:

1. Math of air pollution
2. Trig ratios: updated interactive
3. Resource: Touch Mathematics
4. Math puzzles
5. Friday math movie: How big is infinity?
6. Final thought: Imagination

1. Math of air pollution

My adopted country of Singapore has been badly affected by a choking smoke haze caused by forest fires burning in Indonesia. This article is about the PSI - Pollution Standards Index.

How do we compare pollution caused by different substances and give meaningful health advisories? Singapore's current haze season gives an example. Math of air pollution

2. Trig ratios: updated interactive

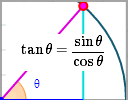Here's an interactive graph where you can investigate some important trigonometric identities. Trig ratios: updated interactive

3. Resource: Touch Mathematics

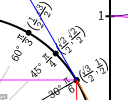Touch Mathematics is an interesting new site containing 2 interactive graphs - one for trigonometry (relating the unit circle with the graphs of trigonometric functions) and derivatives (giving the graphs of the first and second derivatives of some common functions).

There's a lot going on in each graph (probably too much), but it's possible to turn on and off the graphs so you can see better. (In the trigonometry one, click on the function names under the circle to toggle the graphs.)

4. Math puzzles

The puzzle in the last IntMath Newsletter involved finding the limit of the sum and product of 2 given functions.

The interesting thing about this question is that we normally need to assume the limits exist for the given functions before we can say the limit of the sum is the sum of the limits, and likewise for the products. (See a typical explanation here: Limit Properties.)

In the question, the limit at x = 2 does not exist for either of the functions.

But it appears the limits of the sum and product do exist. The limit of the sum is 1 as we approach from either the left or right, and for the product the limit is 0 as we approach from the left or right, as you can see in the graphs below:

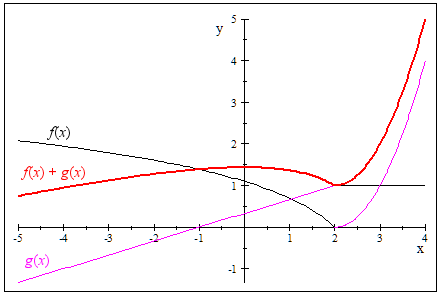
The functions (in black and magenta) and their sum, shown in red.

And now for the product:

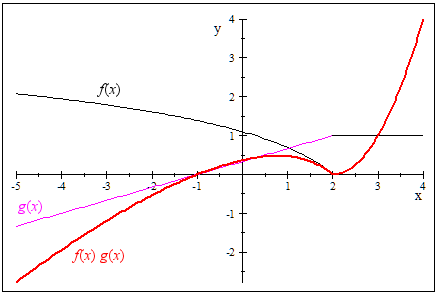
The functions (in black and magenta) and their product, shown in red.

Your responses: Some of you said because the limits don't exist, then the limits of the sums and products don't exist (Nosipho, Sachin).

Others of you (Guido, Douglas, hamid and Tim) agreed with the values shown in the graphs above.

So this is an interesting case. Even though the limits of the component functions don't exist at x = 2, the limits of the sum and product do exist.

New Puzzle

We are given an integer x and told it is the square of a square, and that it has 18 as a factor. What is the least value of x?

Leave your responses here.

5. Friday math movie: How big is infinity?

This is a really interesting mind experiment. You may even find yourself re-thinking your concept of infinity. Friday math movie: How big is infinity?

6. Final thought: Imagination

Sadly, "imagination" is not a word we often hear used in math classrooms. All too often the main thrust is making sure students get the one correct answer. I think math would be a lot more interesting if imagination had more prominence.

This leads me to the following quote by Albert Einstein. If he hadn't used imagination, he would never have come up with the Theory of Relativity.

Your imagination is a preview to life's coming attractions. [Albert Einstein]

Until next time, enjoy whatever you learn.

See the 8 Comments below.