IntMath Newsletter: Conic sections, resources, Ramanujan

By Murray Bourne, 26 May 2016

In this Newsletter:

1. Conic sections interactive applet
2. Resources
3. Math movie: The Man Who Knew Infinity
4. Math puzzles
5. Final thought: personal friends

1. Conic sections interactive applet

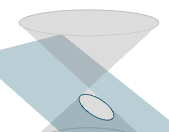This interactive applet allows you to explore the concept of slicing a cone by a plane at various angles and positions, resulting in conic sections. Here's some background and a link to the applet:

Conic sections interactive applet

2. Resources

(a) Learn Desmos

The Desmos Graphing Calculator is a great tool for exploring mathematics concepts. I recently came across the section Learn Desmos, where you can:

Learn how to use the graphing calculator (good for students and instructors, while the next 2 are teacher-focussed)
Explore classroom activities with Desmos
See professional development opportunities using Desmos

(b) John Mighton and JUMP Math

Educators despair over the best way to teach mathematics. Annie Murphy Paul wrote an enthusiastic piece this week about John Mighton and JUMP Math, in "Secrets of a Math Master".

According to the JUMP Math site:

JUMP Math draws on the latest research in cognitive science to build upon the best of math programs from around the world.

(c) Mathcraft

While I'm a big fan of technology, I can undestand the growing popularity of hands-on "maker faire" projects (and adult coloring-in books, too). We become too detached from the physical world the more we are wedded to our devices.

Mathcraft shows how to create mathematical shapes using low-tech tools like pen and paper.

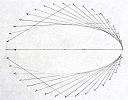On a similar theme to the Conics applet mentioned above, see:

How to Create Concentric Circles, Ellipses, Cardioids & More Using Straight Lines and a Circle

3. Math movie: The Man Who Knew Infinity

This week I had the pleasure of watching The Man Who Knew Infinity, the story of the brilliant Indian mathematician Srinivasa Ramanujan.

With no formal mathematical training, Ramanujan's mathematical breakthroughs were just extraordinary. He could "see" amazing new (and correct) formulas (mostly in number theory topics), similar to the way the great composers could "hear" their compositions before they were ever written down.

The 2015 film chronicles Ramanujan's young adult life in Madras, where he fought to gain recognition for his insights. He eventually is accepted into Cambridge University at the height of British colonial rule over India, which was quite an achievement.

Here's the trailer:

The Man Who Knew Infinity

I especially enjoyed the movie having visited Cambridge last year, and can understand the pleasure Ramanujan gained from walking the same corridors as Isaac Newton did.

Here are some photos (from that trip) of places that appear in the movie:

Isaac Newton statue, Cambridge University

Statue of Isaac Newton in the Chapel, Trinity College, Cambridge

Trinity College, Cambridge

I recommend The Man Who Knew Infinity.

4. Math puzzles

The puzzle in the last IntMath Newsletter asked about converting a fraction into unit fractions, used by the ancient Egyptians.

Correct answers with sufficient explanation (and with the shortest answer of 3 unit fractions) were given by: ct, Don, Rika, Ben and Jess.

Others had longer, but still correct answers. Thomas explained where his 4 unit fractions came from, and Nour did a good job of explaining all her 8 unit fractions.

I suspect the Egyptians always aimed to use the least unit fractions possible.

A note on intuition: In the movie The Man Who Knew Infinity, there's a scene where Hardy asks Ramanujan where his extraordinary formulas come from. Ramanujan, much to the chagrin of the atheist Hardy, says his gods speak to him. Hardy insisted Ramanujan write rigorous proofs for his formulas, stating we can "only believe something we can prove".

Similarly, the IntMath Newsletter encourages those of you who respond to the Math Puzzles to give explanations and insight into the thinking involved. This helps later readers of your solutions.

New math puzzle

Find all real numbers x which satisfy

$\sqrt{\frac{x-1986}{15}}+\sqrt{\frac{x-1987}{14}}+\sqrt{\frac{x-1988}{13}}$

$=\sqrt{\frac{x-15}{1986}}+\sqrt{\frac{x-14}{1987}}+\sqrt{\frac{x-13}{1988}}$

You can leave your responses here.

5. Final thought: personal friends

Such was Ramanujan's love of numbers, that his Cambridge confidant John Littlewood (best known for his achievements in analysis, number theory and differential equations) said:

Every positive integer is one of Ramanujan's personal friends.

— John Littlewood, as recalled in G. H. Hardy (1921), "Obituary Notices: Srinivasa Ramanujan"

Until next time, enjoy whatever you learn.

See the 12 Comments below.

Posted in Intmath Newsletters category - 26 May 2016 [Permalink]

Tags: Graphs, Interactive, Reviews, Technology

12 Comments on “IntMath Newsletter: Conic sections, resources, Ramanujan”

Theophile Habiyambere says:
26 May 2016 at 2:03 pm [Comment permalink]
I really enjoyed the article especially the man who new infinity. Thanks for the article
Murray says:
26 May 2016 at 2:30 pm [Comment permalink]
Hi Ray. Thanks for your interest. The only photos I intended to show were the 2 I included in the Newsletter, so there isn't a missing link.

I was very frustrated when I couldn't take photos in the Wren Library, where Newton's Principia is displayed (also included in the movie).
Don Miller says:
26 May 2016 at 3:29 pm [Comment permalink]
let a=1986,b=15
we will examine each of 9 linear eq., finding values of X
for each. For example, the ratio (under the sq root)
(x-a)/b = (x-b)/a is one of the 9 eq Another is
(x-a)/b =(x-(b-1)/(a+1)
... the last eq is (x-(a+2))/(b-2)= (x-(b-2))/(a+2)
This covers all combinations.
Now back to the first eq
(x-a)/b =(x-b)/a. Solving for x
x= a+b
Repeating this for all eq
x = a +b for each case. Also values of the 6 term are sq(1)+sq(1)+sq(1)=sq(1)+sq(1)+sq(1) X=a+b = 2001
Γιώργος Βαρελάς says:
26 May 2016 at 6:50 pm [Comment permalink]
Restriction: x > 1988 or x = 1988
The solution is: x = 2001
[(2001-1986)/15]^0.5 + [(2001-1987)/14]^0.5 + [(2001-1988)/13]^0.5 =
[(2001-15)/1986]^0.5 + [(2001-14)/1987]^0.5 + [(2001-13)/1988]^0.5 or
(1986/1986)^0.5 +(1987/1987)^0.5 + (1988/1988)^0.5 or
1^0.5 + 1^0.5 +1^0.5 = 1^0.5 + 1^0.5 +1^0.5 or
3 = 3
If: x =2001 + y then
i. If: y > 0:
[{(2001-1986) + y}/15]^0.5 + [(2001-1987) + y}/14]^0.5 + [(2001-1988) + y}/13]^0.5 >
[{(2001-15) + y}/1986]^0.5 + [{(2001-14) + y}/1987]^0.5 + [{(2001-13) + y}/1988]^0.5
[1+(y/15)]^0.5 + [1+(y/14)]^0.5 + [1+(y/13)]^0.5 >
[1+(y/1986)]^0.5 + [1+(y/1987)]^0.5 + [1+(y/1987)]^0.5
Because:
(y/13) >(y/14) >(y/15) >(y/1986) >(y/1987) >(y/1988) and:
1+(y/13)>1+ (y/14)>1+(y/15)>1+(y/1986)>1+(y/1987) >1+(y/1988),
[1+(y/13)]^0.5>[1+(y/14)]^0.5>[1+(y/15)]^0.5>[1+(y/1986)]^0.5>[1+(y/1987)]^0.5>[1+(y/1988)]^0.5,
[1+(y/13)]^0.5+[1+(y/14)]^0.5+[1+(y/15)]^0.5>[1+(y/1986)]^0.5+[1+(y/1987)]^0.5+[1+(y/1988)]^0.5.

ii. If: y < 0:
[{(2001-1986) + y}/15]^0.5 + [(2001-1987) + y}/14]^0.5 + [(2001-1988) + y}/13]^0.5 <
[{(2001-15) + y}/1986]^0.5 + [{(2001-14) + y}/1987]^0.5 + [{(2001-13) + y}/1988]^0.5
[1+(y/15)]^0.5 + [1+(y/14)]^0.5 + [1+(y/13)]^0.5 <
[1+(y/1986)]^0.5 + [1+(y/1987)]^0.5 + [1+(y/1987)]^0.5
Because:
(y/13)<(y/14)<(y/15)<(y/1986)<(y/1987)<(y/1988) and:
1+(y/13)<1+(y/14)<1+(y/15)<1+(y/1986)<1+(y/1987)<1+(y/1988),
[1+(y/13)]^0.5<[1+(y/14)]^0.5<[1+(y/15)]^0.5<[1+(y/1986)]^0.5<[1+(y/1987)]^0.5<[1+(y/1988)]^0.5,
[1+(y/13)]^0.5+[1+(y/14)]^0.5+[1+(y/15)]^0.5<[1+(y/1986)]^0.5+[1+(y/1987)]^0.5+[1+(y/1988)]^0.5.
Adel Jasmin says:
26 May 2016 at 10:22 pm [Comment permalink]
X = 2001
RaySF says:
26 May 2016 at 10:38 pm [Comment permalink]
Murray -
Thanks for all your great newsletters
and the link to the inspiring
film " The Man who knew OO " !.

btw:
under the text:
"Here are some photos"...
you forgot to add the links
to your Cambridge photos?

Best!
Ray
SF
Deborah Tayler says:
27 May 2016 at 12:13 am [Comment permalink]
x = 2001 is a solution, but is it the only one?
Cara van Heerden says:
27 May 2016 at 1:39 am [Comment permalink]
$\sqrt{{\frac{{x}-{1986}}{15}}}+\sqrt{{\frac{{x}-{1986}-{1}}{{15}-{1}}}}+\sqrt{{\frac{{x}-{1986}-{2}}{{15}-{2}}}}=\sqrt{{\frac{{x}-{13}}{1988}}}+\sqrt{{\frac{{x}-{13}-{1}}{{1988}-{1}}}}+\sqrt{{\frac{{x}-{13}-{2}}{{1988}-{2}}}}$

$\sqrt{{\frac{{x}-{1986}}{15}}}=\sqrt{{\frac{{x}-{13}}{1988}}}$
$\frac{{x}-{1986}}{15}=\frac{{x}-{13}}{1988}$
Lidia Carro says:
27 May 2016 at 8:49 pm [Comment permalink]
x = 2001

We notice that
1986+15 = 2001
1987 + 14 = 2001
1988 + 13 = 2001

Replacing x by 2001 in the given equation leads to 3 = 3

We can also work algebraically:

Letting 1986 = a 1987 = a+1 1988 = a+2
15 = m 14 = m-1 13 = m-2

and equating the radicands in pairs, e.g.(x-a)/m = [x-(a+1)]/m-1

we obtain x = m + a
Nour Hlwani says:
28 May 2016 at 4:21 pm [Comment permalink]
To find x value first we reformulate the equation f(x)=0 where:
$f(x)= \sqrt{\frac{x-1986}{15}}+\sqrt{\frac{x-1987}{14}}+\sqrt{\frac{x-1988}{13}}-\sqrt{\frac{x-15}{1986}}-\sqrt{\frac{x-14}{1987}}-\sqrt{\frac{x-13}{1988}}$

Now, geometrically, by plotting f(x) we could find that x is more likely 2001 , which is correct.

If we want to find the root of f(x) in algebra we can use numerical methods for root-finding methods such as the bisection method ,false position method, secant method....etc

The answer is 2001 .
Manju Chowdhury says:
4 Jun 2016 at 4:34 am [Comment permalink]
well on answer is obvious and that is 2001. which is sum of the number subtracted from x plus the number in the denominator. e.g. 1986+15=2001
Anil Bhardwaj says:
26 Jul 2016 at 11:45 am [Comment permalink]
Sir,

This is a great place for me to renew my maths.

Really love it.

Thank you.

IntMath Newsletter: Conic sections, resources, Ramanujan

1. Conic sections interactive applet