IntMath Newsletter: 3D planes, resources, 200 TB math answer

By Murray Bourne, 28 Jun 2016

28 Jun 2016

In this Newsletter:

1. 3D intersection of planes interactive applet
2. Resources: OER and Galileo
3. Math in the news: 200 TB proof
4. Math puzzles
5. Final thought: hustle hard

τ Day (6/28)

Today is Tau Day, a cheeky response to Pi Day, held in March.

1. Intersection of 3 planes at a point: 3D interactive graph

This 3D planes applet allows you to explore the concept of geometrically solving 3 equations in 3 unknowns. Here's some background and a link to the applet.

Intersection of 3 planes at a point: 3D interactive graph

2. Resources

(a) Open Educational Resource Commons

This resource is appropriate for both students and teachers.

Open Educational Resources provides free text books (in PDF) and other resources in a wide variety of topics (including science, arts & humanities and technical areas.)

The mathematics section had some neat materials, including articles on estimation, statistics, calculus and trigonometry.

There's also a STEM Literacy section, which states in the welcome:

A STEM literate person considers how STEM can improve the social, cultural, economic, and environmental conditions of their local and global communities.

(b) Galileo: Inquiry-based learning

Galileo.org is mostly aimed at teachers, and provides some interesting inquiry-based resources in mathematics and science, including lesson designs and classroom examples. There are also articles and suggestions regarding technology-based approaches to teaching.

3. Math in the news

Consider a 3,4,5 Pythagorean triple, as follows. We color 2 of the squares red, and the other blue.

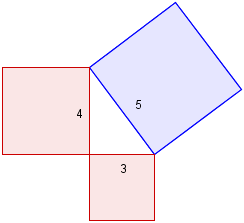
3-4-5 triangle - Ramsey Theory

Next, construct a 5,12,13 right triangle based on that blue 5×5 square, as follows.

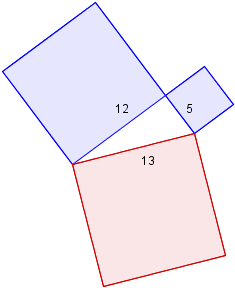
5-12-13 triangle - Ramsey Theory

We choose blue and red for the colors of the other two triangles. We could have swapped those 2 colors, but we can't have all blue, or all red.

What we're doing is demonstrating Ronald Graham's Boolean Pythagorean Triples problem, which asks if it's possible to color the squares given by all the Pythagorean triples using exactly two colors only.

With small numbers like the ones above, it seems quite straightforward, but as the numbers get bigger we may be forced to choose a color for one of the triples based on a previous condition, only to find the current set doesn't allow that color (because we may end up with all blue, or all red squares).

Graham offered a $100 prize to anyone who could solve the problem (that is, can it be done for all Pythagorean triples?).

Last month, researchers Marijn Heule from the University of Texas, Victor Marek from the University of Kentucky, and Oliver Kullmann from Swansea University used a Stampede supercomputer to solve it.

The answer is a 200 terabyte file which is not human-readable. It would take you 30,000 hours just to download it!

So is it a proof?

This is a great example of how modern mathematics is becoming irrevocably entwined with computers. There has been some interesting discussion about whether such a large file can be considered a "proof" at all. It can be read by computers and verified by computers, but we humans can't really step through such a proof and check its validity.

Graham was happy with the answer and the researchers got their $100.

More information here:

The world's largest maths problem has been solved, and it takes up 200 TB

4. Math puzzles

The puzzle in the last IntMath Newsletter involved solving an equation with 6 square roots and 6 fractions.

Correct answers with sufficient explanation (which included some reasoning about the number of solutions) were given by: Don, Giorgos, Lidia and Nour. Other partially correct answers (not including the uniqueness part) were given by Cara and Manju.

Nour's approach was to graph it (after substracting the 3 right-hand terms from both sides). He would have seen something like this:

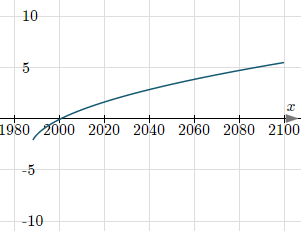
solution of a equation with 6 square roots
Graphical solution of equation

The graph is discontinuous, since it has no value for x < 1988. It continues on beyond 2100 getting less and less steep, but never crosses the x-axis again. (It looks something like a half-parabola on its side.) So there was a unique solution.

New math puzzle

At a plant stall, I can buy 8 xerophytes for $1, yams for $1 each and zinnias for $10 each. I grab a selection of plants and find at the checkout that I have exactly 100 plants and they will cost me $100. How many of each type did I get?

You can leave your responses here.

5. Final thought: Hustle hard

I came across this gem on Twitter recently, from "joy_ding.app".

We would achieve a lot more if we increase our output (or effort, learning time, or reading time) by 1% per day, as opposed to reducing it by 1% per day!

Until next time, enjoy whatever you learn.

See the 18 Comments below.

Posted in Intmath Newsletters category - 28 Jun 2016 [Permalink]

Tags: Graphs, Interactive, Technology

18 Comments on “IntMath Newsletter: 3D planes, resources, 200 TB math answer”

Γιώργος Βαρελάς says:
29 Jun 2016 at 12:03 am [Comment permalink]
x = xerophytes = 72,
y = yams = 21,
z = zinnias = 7

x/8 + y + 10*z = 100 (1)
x + y + z = 100 (2)
0 < x < 100, 0 < y < 100, 0 < z < 100

(1), (2):
(7*x)/8 = 9*z or
7*x = 72*z
then
x = 72, z = 7
and
y = 21
Kai says:
29 Jun 2016 at 12:33 am [Comment permalink]
From the cost of the plants, we get the following equation:
$\frac{1}{8}x + y + 10 z = 100$
and from the total number of plants, we have:
$x + y + z = 100$

Solving the second equation for $x$ and substituting into the first (and multiplying the whole thing by 8), we get:
$7 y + 79 z = 700$

This equation has infinitely many solutions in $y$ and $z$ , but we are only interested in integer solutions (can't buy partial plants), making this a Diophantine Equation. More specifically, we want non-negative integer solutions, because we cannot buy negative plants. Using the Euclidean Algorithm, we can find all of the non-negative integer solutions $(y,z)$ : $(100, 0)$ and $(21, 7)$ .

Plugging these into either of the first 2 equations, we get solutions $(x,y,z)$ of:
$(0,100,0)$ and $(72,21,7)$

Assuming that "a selection of plants" means that you got some of each (each is greater than zero), then we eliminate the trivial solution of buying 100 yams, and the only possible remaining solution is:
72 xerophytes
21 yams
7 zinnias
Nour Hlwani says:
29 Jun 2016 at 8:11 am [Comment permalink]
First of all,
Let x = quatity bought of xerophytes.

And using the rule of 3..

8 xero --> 1$
X --> $\frac{X}{8}$ $

For yams.
Let y = quatity bought of yams = y $
And
z = quantity bought of zinnias = 10z $

And conditions are:

$x + y + z = 100$
$\frac{x}{8} + y + 10z = 100$

Solving it as a matrix:
1 1 1 : 100
1/8 1 10 : 100

Gives:
(x,y,z) = (72n , 100-79n , 7n) where n is an integer because x y z are positive integers
So y>=0 then n=< 100/79 (arround 1.26)

Then n could be either 0 or 1

For n=0
(x,y,z) = (0 , 100 , 0)
100 yams which costs 100$

For n=1
(x,y,z) = (72 , 21 , 7)

72 xerophytes ,21 yams and 7 zinnias .. their sum is 100 and they cost 100$.
Lidia Carro says:
29 Jun 2016 at 9:15 am [Comment permalink]
Let x be the number of xerothypes,
y the number of yams and
z the number of zinnias

Then we can form the following two simultaneous equations

x + y + z = 100
(1/8)x + y + 10z = 100

Subtracting the equations we obtain

(7/8)x - 9z = 0
(7/8)x = 9z
(7/72)x = z ,we try x = 72 in this equation and

obtain z =7 which then implies that y = 100 - 79
y = 21

Then we got 72 xerotypes, 21 yams and 7 zinnias

Checking the money statement: 72 xerothypes cost $9 (72:8)
21 yams cost $21
7 zinnias $70
Total: $9 + $21 +$70 = $ 100
Don Miller says:
29 Jun 2016 at 10:34 am [Comment permalink]
given: X+Y+Z = 100, x+y+z = $100, X= number of xero,Y= number of yams, Z=number of zinnias,x=cost of xero(dollars),y=cost of yams,z=cost of zinnias.Cost of each xero =$.125,yam $1, zinnias $10

First X must be multiple of 8; 8,16,24,...56,64,72,80. Other values would violate integer cost values.By trial/error I tried X= 56. Y+Z=100-56,Y*1+10*Z=100-56/8. Subtracting gives 9*Z=93, z is not a mult of 10
Try X=72,Y+Z=100-28,y+10*Z=100-72/8 =91. Subtracting give 9Z=63
Z=7. 72 +Y+7=100,Y=100-7-72=21,$ check 9 +21+10*7 =100 QED
X=72,Y=21,Z=7 ANSWER
Shihab says:
29 Jun 2016 at 1:43 pm [Comment permalink]
Solution:
x= $9, Items= 72
y= $21, items= 21
Z= $70, Items= 7
...=$100,.....= 100
Rene says:
30 Jun 2016 at 1:34 am [Comment permalink]
100 yams?

I know that's not the answer you want.
Rasheed Sindhi says:
2 Jul 2016 at 11:35 am [Comment permalink]
Let the number of xerophytes,yams and zinnias are x,y and z respectively.
According to the given
x+y+z=100...................A
price of xerophytes 1/8 $,so price of x xerophytes will be (1/8)x $
Similarly prices of y yams and z zinniats will be y $ and 10z $
Total price is 100$
Hence. x/8+y+10z=100.................B
A-B gives 7x/8-9z=0
7x=72z
X=72z/7....................................C
Since x is a whole number(number of plant may not be fraction)
7 divide 72 or 7 divides z
But 7 does not divide 72
So 7 must divede z i-e z is multiple of 7
z=0,7,14...
Assuming that number of plants of any kind is not equal to 0
and we can purchase at most 10 zinniats from 100$,this implies
0 < z < 10 So z=7 (The above inequality excludes all multiples except 7 itself) Putting z=7 In C x=72*7/7=72 Putting x=72 and y=7 in A 72+y+7=100 y=21 Hence number of xerophytes, yams and zinnias are 72, 21 and 7
Rasheed Sindhi says:
3 Jul 2016 at 5:18 pm [Comment permalink]
Dear Murray
A suggestion for puzzle section: puzzles should be numbered for
the puruse of refernce.The present referencing way is too complicated.
Murray says:
3 Jul 2016 at 7:08 pm [Comment permalink]
@Rasheed: Thanks for your feedback.

Each Newsletter has one puzzle only. The submitted answers are commented on in the following Newsletter (with links going back to the puzzle and answers referred to). Hope it makes sense.

I'll add a date in future answer comments and I hope that will make it clearer.
Rasheed Sindhi says:
3 Jul 2016 at 7:37 pm [Comment permalink]
Thanks a LOT!
HELENA NAYAR says:
4 Jul 2016 at 11:28 pm [Comment permalink]
From the information given we can form 2 equations:
x + y + z = 100, where x,y,z represent the #s.
x/8 + y + 10z = 100.
x + 8y +80z = 800
.................
7y + 79z = 700
y = 100 - (79/7)z.
The only value that z can take is 7. hence y = 21 and x = 72.
Colin Morrison says:
12 Jul 2016 at 6:55 pm [Comment permalink]
72x + 21y +7z by induction. Key is 10-8=2. Might be other solutions but can't prove it.
Chris Buchanan says:
20 Jul 2016 at 9:54 pm [Comment permalink]
no. bal: ${x}+{y}+{z}={100}$

money bal: $\frac{x}{8}+{y}+{10}{z}={100}$

no third equation

Step through z from 0 to 10 until x and y are whole numbers
Wolfram Alpha makes life very easy

${x}={72},{y}={21},{z}={7}$
Chris Buchanan says:
22 Jul 2016 at 6:47 pm [Comment permalink]
I missed the obvious: ${x}={0},{y}={100},{z}={0}$

xi = []
yi = []
zi = []

for z in range(0,10):
def solv(var):
x,y = var
return [y + x + z - 100,
x/8 + y + 10*z - 100]
ans = fsolve(solv,[1,1])
if ans[0] % 1 == 0:
xi.append(ans[0])
else:
xi.append(0)
if ans[1] % 1 == 0:
yi.append(ans[1])
else:
yi.append(0)
zi.append(z)

print (xi)
print (yi)
print (zi)
Chris Buchanan says:
22 Jul 2016 at 7:06 pm [Comment permalink]
Better Python:

for z in range(0,10):
def solv(var):
x,y = var
return [y + x + z - 100,
x/8 + y + 10*z - 100]
ans = fsolve(solv,[1,1])
if ans[0] % 1 == 0:
print ('x =', ans[0], 'y =', ans[1])
if ans[1] % 1 == 0:
print ('x =', ans[0], 'y =', ans[1])
Chris Buchanan says:
22 Jul 2016 at 7:20 pm [Comment permalink]
Best Python:

for z in range(0,10):
def solv(var):
x,y = var
return [y + x + z - 100,
x/8 + y + 10*z - 100]
ans = fsolve(solv,[1,1])
if ans[0] % 1 == 0 and ans[1] % 1 != 0:
print ('x =', round(ans[0]), ' y =', round(ans[1]), ' z =', z)
if ans[1] % 1 == 0:
print ('x =', round(ans[0]), ' y =', round(ans[1]), ' z =', z)
matlunix says:
4 Aug 2016 at 9:01 pm [Comment permalink]
By inspection:
We can form two set of equations:

* 8 x's cost $1 => 1 x costs $1/8 = (1/8)x
* cost calculation of y is straightforward => 1 y costs $1
* cost calculation of z is 10z
The equation can be laid out as follow: x/8+y+10z = 100
Let x/8 = X and 10z = Z. Constructing a sample matrix for the number of plants bought and its cost
----------------------
# of plants | cost
----------------------
x:64 |x/8:$8
y:30 |30y:$30
z:6 |10z:$60
----------------------
Total:100 |$98
----------------------

This does not satisfy our condition. The maximum limit for buying so that our costs are covered are - x=[1,9) and z=[1,7]. Applying the maximum number in both x's and z's we have:

----------------------
# of plants | cost
----------------------
x:72 |x/8:$9
y:21 |21y:$21
z:7 |7z :$70
----------------------
Total:100 |$100
----------------------

IntMath Newsletter: 3D planes, resources, 200 TB math answer

τ Day (6/28)

1. Intersection of 3 planes at a point: 3D interactive graph