Graphs using free math software

[Updated Dec 2016.]

Being able to sketch graphs on paper is an important skill, but I'm wondering about the future of this. There are now many free (or cheap) graphing tools available and I am surprised so few students actually use them (or are allowed to use them).

Let's have a look at some of the available math graphing tools.

Graphics Calculators

Here are the Texas Instruments TI-83 (left) and Hewlett-Packard HP 40gs (right) calculators.

Graphics calculators are handy, but the screen size is small and there is usually no scale on the axes. Cost is often prohibitive, at around US$100.

Online Graphers

Here's a few places where you can graph your curve - for free!

My favorite in this space is:

• Desmos

Don't miss The Daily Desmos for some cool graphs.

The next example uses Scalable Vector Graphics, right here on IntMath.

• Plot your own SVG Math Graphs

For another grapher based on a well-known SVG grapher, see: JSXGraph function plotter.

The following are also free offerings (some suggested by readers). I've presented them roughly in order of preference.

• Wolfram|Alpha (produces a graph image, which can be converted to CDF interactive if you have the pricey Mathematica)
• GraphSketch.com (image-based)
• Good Calculators (canvas- and javascript-based)
• GraphFree (image-based)

Downloadable software apps

Here are some of my favorites. In each case you need to download and install the software.

• GeoGebra (Free. I wrote a review of GeoGebra which shows how to get started with it.)
• Graph 4.4.2 (Free. Small download, from cnet.com)

Requires payment:

• Scientific Notebook (US$90, but does much more than a graphics calculator. It's a full computer algebra system, but much cheaper than MatLab or Mathematica, etc.)

Some problems with using graphics software

If you don't have a good idea of what a function should look like before your use a graphics package, you can have all sorts of problems.

Here's an example of a function which catches out the unaware.

Let's graph it on Geogebra.

Hmmm - it appears to be empty. Is there an error? What's going on?

We zoom out a few times and start to see 2 curves. Once again, is there a mistake? Why 2 curves?

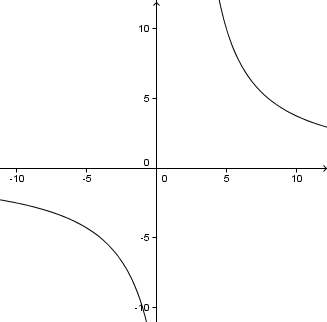
I zoomed out because I had a good idea in my head what the graph should look like. Since I couldn't see either of the 2 arms of this curve, and because of the 30 in the denominator, I knew I had to zoom out.

If I left my graph at that, I would still not have a good idea of what the function looks like. I have not chosen a view that shows the crucial features of this graph.

The default view in Geogebra was too close to the origin (0, 0) to see any of the curve.

Let's have another go, this time using Scientific Notebook. This is what I get when I try to graph the curve.

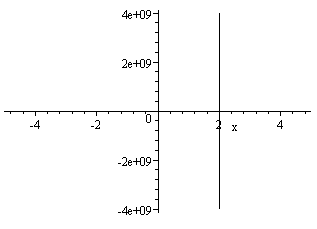
I get a vertical line passing through 2 on the x-axis. But notice the scale on the y-axis. The number "4e+09" actually means 4 × 10⁹ or 4 billion. So Scientific Notebook recognizes that there are very large values of y involved in this function, and has shown us the limits of its internal coding.

This time if we zoom in, we can start to see the graph appearing as before. But I need to know to zoom in, otherwise I would miss it altogether.

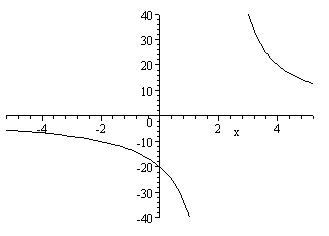
What was that vertical line that appeared before? Was it a mistake? Why did it disappear when we zoomed in?

Next, we use my SVG Grapher. It's similar to Geogebra in that its default view misses the curves, but is also similar to Scientific Notebook in that it shows a vertical line through 2 on the x-axis.

When we zoom out a bit, this is what we get.

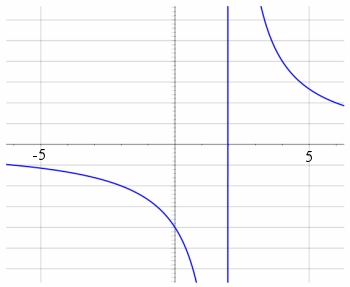
We are still not showing all the vital features of the graph, and that vertical line is still there. What's that about?

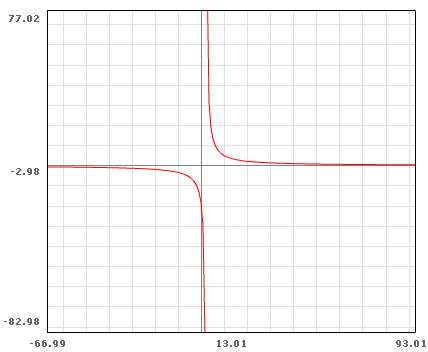
Next, I tried the Flash Math Grapher. Once again I needed to do some zooming. The x- and y- scales are strange (multiples of 13.01??, and is that the x-axis or the line y = -2.98?) , but at least I can get a pretty good view.

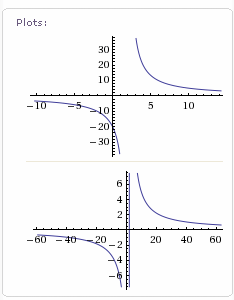
Next, let's call in the big guns. Wolfram|Alpha gives us the following 2 graphs when we put our function in their search box (and they give us a lot more information about the function).

This time we get intelligent graphs that have appropriate x- and y- scales and actually show the curves. Note the first one does not have a vertical line through 2, but the second one does. Why?

That vertical line through x = 2

When the software draws the graph, it chooses regularly-spaced x-values and substitutes them into the function, plots the resulting dots and joins them.

In the above examples that have a vertical line, it means the software has chosen a value just slightly less than 2 (which will give a very small, negative value for y) and another one just slightly more than 2 (which gives a very large positive value for y).

Here's an exaggerated version of what it's doing (using only a very few data points joined by straight lines).

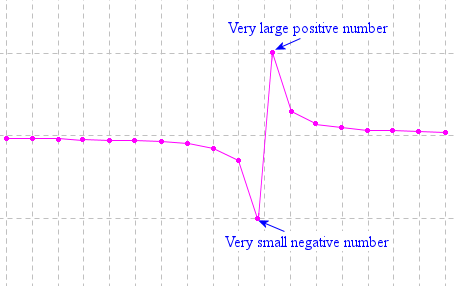
If the x-value chosen is exactly 2, the software will normally just skip that value (since it will return a "division by 0" error). The (almost) vertical line should not be included in the graph, since we cannot have x = 2 (this function is undefined for x = 2 since the bottom of the fraction would be zero).

This gap in the graph is called a discontinuity. It should be a gap - not joined by a line as above.

Some software handles this situation gracefully (like the Wolfram|Alpha example) while in others, you need to either understand why the vertical line is there, or in some cases, you can elect to include discontinuities or not.

Best answer

Here's probably the best way to display the graph of this function.

Our graph has 2 asymptotes. When a curve gets closer and closer to a line but does not touch it, that line is called an asymptote

The first asymptote is the x-axis and the other is the vertical line, x = 2, which I drew using a dashed line of a different color (since it is not part of the graph).

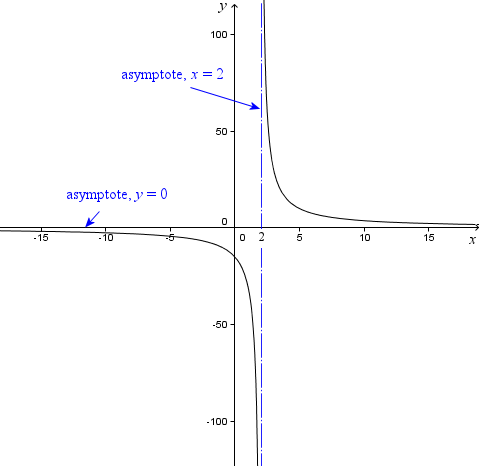
I have shown the 2 asymptotes clearly and I have also labeled the x- and y-axes.

Here's the function again for convenience.

I knew the graph was going to involve asymptotes since the x-variable is in the denominator (and we can't have 0 in the denominator) and also considering when x gets really big, the value of the function will be really small.

If I didn't know this (from graphing many of them on paper), I would have made a mess of graphing my function on a computer.

Graphing software and the future

Will graphing software change what we do in classrooms? Should it? Is it really necessary to sketch graphs on paper still?

If you can draw a quick sketch of a function on paper, it certainly helps your understanding for many types of math problems. The conclusion from above is that it is certainly worthwhile to have a good sense of what a graph should look like before graphing it using software, so we can manipulate the settings to show the graph properly.

See the 23 Comments below.