IntMath forum | Plane Analytical Geometry
Fillet radius for eyeglass lens [Solved!]
Pritam 11 Feb 2016, 08:20
My question
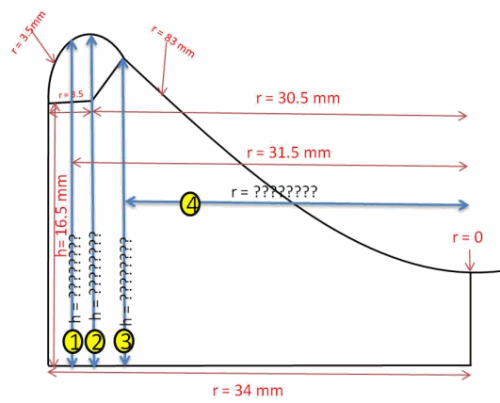
i want to find heights as given in the image. i have apply radius fillet command with one line and one arc radius is 83mm
Fillet radius is 3.5mm
Inner curve radius is 83mm
Filler starting point height is 16.5mm
Part radius is 34mm
I have one problem I want to find out this 4 thing using this available value
I am trying to give fillet radius of 3.5mm with line and arc of 83mm radius
no 1 I have r = 31.5mm then how to find h=??????
no 2 I have three value h=16.5mm , r = 30.5mm and second fillet r = 3.5mm then how to find h= ?????
no 3 I have only radius 83mm and fillet radius 3.5mm and h = 16.5 mm the what is 3 and 4 value
What is intersection point height no 3 with radius 3.5 and h = 16.5(starting point of fillet) and radius = 83mm
can you pls help me out for this question
Thanking You
Pritam
Relevant page
3. The Circle
What I've done so far
I know the formula for a circle, but I can't see how to use that in my problem.
X
<img src="/forum/uploads/imf-3657-lens-image-1.png" width="500" height="403" alt="plane-analytic-geometry" />
i want to find heights as given in the image. i have apply radius fillet command with one line and one arc radius is 83mm
Fillet radius is 3.5mm
Inner curve radius is 83mm
Filler starting point height is 16.5mm
Part radius is 34mm
I have one problem I want to find out this 4 thing using this available value
I am trying to give fillet radius of 3.5mm with line and arc of 83mm radius
no 1 I have r = 31.5mm then how to find h=??????
no 2 I have three value h=16.5mm , r = 30.5mm and second fillet r = 3.5mm then how to find h= ?????
no 3 I have only radius 83mm and fillet radius 3.5mm and h = 16.5 mm the what is 3 and 4 value
What is intersection point height no 3 with radius 3.5 and h = 16.5(starting point of fillet) and radius = 83mm
can you pls help me out for this question
Thanking You
Pritam
Relevant page
<a href="/plane-analytic-geometry/3-circle.php">3. The Circle</a>
What I've done so far
I know the formula for a circle, but I can't see how to use that in my problem.
Re: Fillet radius for eyeglass lens
Murray 11 Feb 2016, 22:18
Hello Pritam
It depends on whether this is a one-off problem (you just need to know the numerical values for this situation) or whether you need to be able to solve it algebraically for many different radii and lengths.
If it is the former case, then GeoGebra is your best friend.
I have made some assumptions:
(1) You really meant the intersection of the smaller and larger arcs to be tangential (that is, smooth)
(2) Your larger curve should have been a circular arc (in your diagram, it looks parabolic)
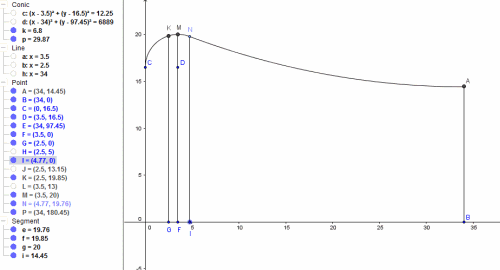
You can get all the values you need from this screen shot.
For example, N is the intersection point of the smaller fillet arc and the larger arc. It's y-value is 19.76, so that is your value "3" in your image.
If you need to do it algebraically, then you would need to find:
(1) The centre point of the larger arc
(2) The equation of the larger arc
(3) The equation of the smaller arc
(4) The intersection point of the 2 arcs using simultaneous equations
But graphically is much easier and quicker, especially with GeoGebra.
Hope it helps.
X
Hello Pritam
It depends on whether this is a one-off problem (you just need to know the numerical values for this situation) or whether you need to be able to solve it algebraically for many different radii and lengths.
If it is the former case, then <a href="http://www.geogebra.org/">GeoGebra</a> is your best friend.
I have made some assumptions:
(1) You really meant the intersection of the smaller and larger arcs to be tangential (that is, smooth)
(2) Your larger curve should have been a circular arc (in your diagram, it looks parabolic)
You can get all the values you need from this screen shot.
For example, N is the intersection point of the smaller fillet arc and the larger arc. It's y-value is 19.76, so that is your value "3" in your image.
<img src="/forum/uploads/imf-4312-lens-geogebra-solution.png" width="500" height="270" alt="plane-analytic-geometry" />
If you need to do it algebraically, then you would need to find:
(1) The centre point of the larger arc
(2) The equation of the larger arc
(3) The equation of the smaller arc
(4) The intersection point of the 2 arcs using simultaneous equations
But graphically is much easier and quicker, especially with GeoGebra.
Hope it helps.
Re: Fillet radius for eyeglass lens
Pritam 12 Feb 2016, 12:15
Hello Sir.
Thank you for the reply sir.
It is smaller and larger arcs tangential intersection point.
both arc is circle not parabola.
I need to find this by equation . here i have attached the new drawing.
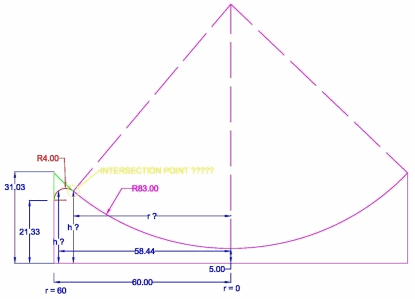
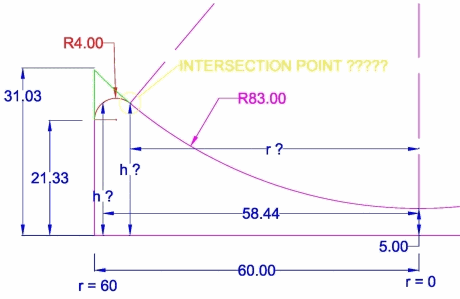
I am trying to apply fillet radius to my part for that i need formula to calculate this height and intersection point at which radius. so that i can apply in my software.
I have only this much data available for calculation
Bigger Arc Radius = 83 mm
Fillet Arc Radius = 4 mm
Starting Point of Fillet Arc = 21.33 mm
Total Height of part or inter section of line and big arc = 31.03
as i under stand you told me to calculate arc length of small and large arc but how can i with out theta how can i calculate it sir?
I need formula to calculate this question mark.
Thanking you
Pritam
X
Hello Sir.
Thank you for the reply sir.
It is smaller and larger arcs tangential intersection point.
both arc is circle not parabola.
I need to find this by equation . here i have attached the new drawing.
<img src="/forum/uploads/imf-4721-filletradius.png" width="415" height="290" alt="plane-analytic-geometry" /><img src="/forum/uploads/imf-4743-filletradius1.png" width="460" height="299" alt="plane-analytic-geometry" />
I am trying to apply fillet radius to my part for that i need formula to calculate this height and intersection point at which radius. so that i can apply in my software.
I have only this much data available for calculation
Bigger Arc Radius = 83 mm
Fillet Arc Radius = 4 mm
Starting Point of Fillet Arc = 21.33 mm
Total Height of part or inter section of line and big arc = 31.03
as i under stand you told me to calculate arc length of small and large arc but how can i with out theta how can i calculate it sir?
I need formula to calculate this question mark.
Thanking you
PritamRe: Fillet radius for eyeglass lens
Murray 13 Feb 2016, 02:11
Hello Pritam
All your values changed!
With the new values, here is your solution:
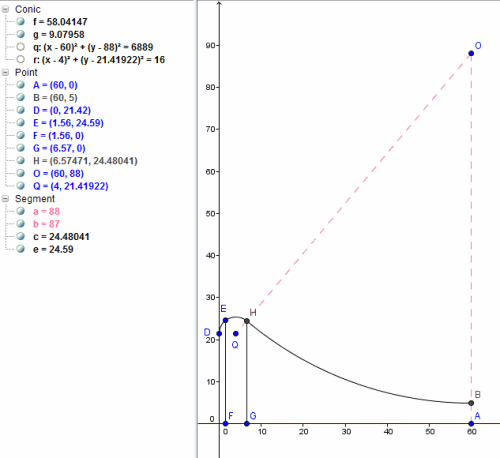
I don't believe the value "21.33" in your diagram is correct. (It is actually 21. 4192).
I didn't actually say to calculate the arc length. I said you'll need to find the equations of the small and large arcs (that is, the equations of the larger circles that the arcs are part of).
The large one is straightforward, but you can't find the small one without knowing its height from the x-axis.
So you'll have 3 unknowns:
(1) h, the height of the smaller circle from the x-axis
(2) x0, the x-coordinate of the intersection point (H in my latest diagram)
(3) y0, the y-coordinate of the intersection point
Another hint is the segment OH when extended will pass through Q (the center of the small circle). How do we know? Because it is a tangential join at that point, so the angle of the normal to both curves must be 90 degrees, and this the 2 radii at that point form a straight line).
So we can find the equation of the line OQ (which will include the variable h).
Now you will have 3 equations in 3 unknowns.
Solving that will give you the height h, and the desired point H.
As long as your software can handle substitutions, it should work out fine.
Let me know if you need more help.
BTW, what is all this for?
X
Hello Pritam
All your values changed!
With the new values, here is your solution:
<img src="/forum/uploads/imf-4945-lens-image-2.png" width="500" height="458" alt="plane-analytic-geometry" />
I don't believe the value "21.33" in your diagram is correct. (It is actually 21. 4192).
I didn't actually say to calculate the arc length. I said you'll need to find the equations of the small and large arcs (that is, the equations of the larger circles that the arcs are part of).
The large one is straightforward, but you can't find the small one without knowing its height from the x-axis.
So you'll have 3 unknowns:
(1) h, the height of the smaller circle from the x-axis
(2) x0, the x-coordinate of the intersection point (H in my latest diagram)
(3) y0, the y-coordinate of the intersection point
Another hint is the segment OH when extended will pass through Q (the center of the small circle). How do we know? Because it is a tangential join at that point, so the angle of the normal to both curves must be 90 degrees, and this the 2 radii at that point form a straight line).
So we can find the equation of the line OQ (which will include the variable h).
Now you will have 3 equations in 3 unknowns.
Solving that will give you the height h, and the desired point H.
As long as your software can handle substitutions, it should work out fine.
Let me know if you need more help.
BTW, what is all this for?
Re: Fillet radius for eyeglass lens
Pritam 13 Feb 2016, 15:55
Hello Sir,
First i brief you my self .i am 33 year old. I was a botany student in India so am very very bed in math.i am a very good computer programmer. Form last two year i am started study so many books to developing one ophthalmic machine that was only made by Germany and USA(Lens Generator (lathe).
this machine is so many calculation of sin and cos values. I have develop that machine almost 90% to 95% some of the correction is required for that.
one of the correction is Lens Fillet on the Edge. for that i need some calculation equation.
today i have try some trigonometry function (B2 = C2-A2) for that i think i have get the value but it is right or not i am not sure.
i just add that value in the h + Adjacent Leg = 21.4192+ Adjacent Leg = so i found my total height.
but where is the intersection point height and form which point i have to change my cutter direction i need that point sir. that is H sir . and up to which theta angle i have to calculate this function i am not sure.
even if i get the radius value where the H is i think i can calculate all the thing. if possible please suggest me formula to calculate H value radius and height. as my fillet radius is every time same but my lens radius will change as per the prescription

Here are 2 videos explaining it.
Lens profile cutting 1 - YouTube
How Lenses Are Made - YouTube
X
Hello Sir,
First i brief you my self .i am 33 year old. I was a botany student in India so am very very bed in math.i am a very good computer programmer. Form last two year i am started study so many books to developing one ophthalmic machine that was only made by Germany and USA(Lens Generator (lathe).
this machine is so many calculation of sin and cos values. I have develop that machine almost 90% to 95% some of the correction is required for that.
one of the correction is Lens Fillet on the Edge. for that i need some calculation equation.
today i have try some trigonometry function (B2 = C2-A2) for that i think i have get the value but it is right or not i am not sure.
i just add that value in the h + Adjacent Leg = 21.4192+ Adjacent Leg = so i found my total height.
but where is the intersection point height and form which point i have to change my cutter direction i need that point sir. that is H sir . and up to which theta angle i have to calculate this function i am not sure.
even if i get the radius value where the H is i think i can calculate all the thing. if possible please suggest me formula to calculate H value radius and height. as my fillet radius is every time same but my lens radius will change as per the prescription
<img src="/forum/uploads/imf-5323-filletproblem2.png" width="460" height="362" alt="plane-analytic-geometry" />
Here are 2 videos explaining it.
<a href="https://www.youtube.com/watch?v=h6kPEugdGA">Lens profile cutting 1 - YouTube</a>
<a href="https://www.youtube.com/watch?v=E91a7nBkkR8">How Lenses Are Made - YouTube</a>Re: Fillet radius for eyeglass lens
Murray 14 Feb 2016, 06:14
Hi again
OK, this is how you can solve your problem:
(1) The equation of the small circle is:
`(x-4)^2+(y-k)^2=16`
We know the center is `(4, h)` and the radius is `4`.
See here for background on circles:
3. The Circle
(2) The equation of the large circle is
`(x-60)^2+(y-88)^2=6889`
Its center is `(60, 80)` and radius is `83`.
(3) The equation of the line OQ is given by:
`y=88+((88-h)/56)(x-60)`
This comes from using the formula
`y - y1 = m(x - x1)`
See 2. The Straight Line
Those are the 3 equations in 3 unknowns I was talking about.
Do you think you can go from there?
X
Hi again
OK, this is how you can solve your problem:
(1) The equation of the small circle is:
`(x-4)^2+(y-k)^2=16`
We know the center is `(4, h)` and the radius is `4`.
See here for background on circles:
<a href="/plane-analytic-geometry/3-circle.php">3. The Circle</a>
(2) The equation of the large circle is
`(x-60)^2+(y-88)^2=6889`
Its center is `(60, 80)` and radius is `83`.
(3) The equation of the line OQ is given by:
`y=88+((88-h)/56)(x-60)`
This comes from using the formula
`y - y1 = m(x - x1)`
See <a href="/plane-analytic-geometry/2-straight-line.php">2. The Straight Line</a>
Those are the 3 equations in 3 unknowns I was talking about.
Do you think you can go from there?
Re: Fillet radius for eyeglass lens
Pritam 14 Feb 2016, 20:10
Thanks.
I tried to do it on paper but it was horrible!
I found this Wolfram|Alpha widget: System of Equations Solver
Using that, I got
`h = 21.4192`
`x = 6.5747`
`y = 24.4804`
So the center of the small circle is `(4,21.4192)`. The point of intersection H is `(6.5747, 24.4804)`, which is the same as your answers.
Thanks again very much for your help.
Regards
Pritam
X
Thanks.
I tried to do it on paper but it was horrible!
I found this Wolfram|Alpha widget: <a href="http://www.wolframalpha.com/widgets/view.jsp?id=ae438682ce61743f90d4693c497621b7">System of Equations Solver</a>
Using that, I got
`h = 21.4192`
`x = 6.5747`
`y = 24.4804`
So the center of the small circle is `(4,21.4192)`. The point of intersection H is `(6.5747, 24.4804)`, which is the same as your answers.
Thanks again very much for your help.
Regards
Pritam
Related Plane Analytical Geometry questions
- Re: Finding the Area with Pythagoras's theorem [Solved!]
In the "relevant page" in your question, you'll see a discussion about 30-60 triangle. That... Murray 23 May 2020, 11:08
- Conic rotation [Solved!]
Determine the graph identity y^2+8x=0 for phi=6/pi and write an equation of the rotated or... EW 03 Mar 2020, 06:40
- The Circle [Solved!]
Check out the url below. Under Plane Analytical Geometry - The Circle.
The final line... phinah 29 Apr 2019, 01:59
- Center and Radius of Circle [Solved!]
On your site, the Plane Analytical Geometry Chapter, section 3 - The Circle, at... phinah 08 Apr 2019, 03:31
- Plane analytical geometry apply in real life? [Solved!]
Comments: How is plane analytical geometry apply in real life?
What are type of real life... Rachel 24 Nov 2015, 10:45
Plane Analytical Geometry lessons on IntMath
top





