What did Newton originally say about Integration?
By Murray Bourne, 22 Jul 2010
Most of us learn about math from modern textbooks, with modern notation and often divorced from the historical original. No wonder people think math is a modern invention that's only designed to torture students!
Isaac Newton wrote his ideas about calculus in a book called The Principia (or more fully, Philosophiae Naturalis Principia Mathematica, which means "Mathematical Principles of Natural Philosphy"). This was an amazing book for the time (first published in 1687), and included his Laws of Motion.
Newton wrote his Principia in Latin. It was common for mathematicians to write in Latin well into the 19th century, even though other scientists were writing (perhaps more sensibly) in their native tongues (or in commonly spoken languages like French, German and English).
Let's look at one small part (which he named "Lemma II") of Newton's work, from the first English translation made in 1729. You can see all of that translation here, thanks to Google Books (go to page 42 for Lemma II):
1729 English Translation of Principia
The problem below was very important for scientists in the late 17th century, since there were pressing problems in navigation, astronomy and mechanical systems that couldn't be solved with existing inefficient mathematical methods.
Some explanations before we begin:
- A Lemma is a statement that has been proven, and it leads to a more extensive result.
- In old English, the ∫ sign is an "S". The first word where this appears below is "in∫crib'd", which we would write as "inscribed". (Note the "s" used for plural nouns is the same as our 's".) The elongated S symbol ∫ came to be used as the symbol for "integration", since it is closely related to "sum".
- "Dimini∫hed" is "diminished", and means "get smaller".
 is "&c" which we would write these days as "etc" (et cetera)
is "&c" which we would write these days as "etc" (et cetera) - "Augmented" means "get bigger".
- "Ad infinitum" is Latin for "keep doing it until you approach infinity".

This is the diagram that is referred to in the above text.
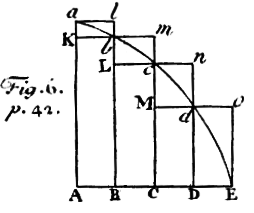
Explanation
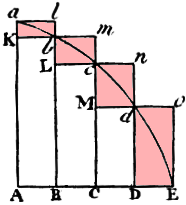
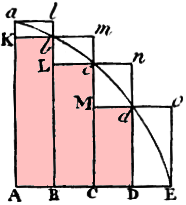
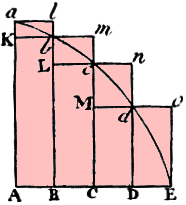
Let's go through it one concept at a time, with appropriate tweaks to the diagram. We are trying to find the area between a curve abcdE and 2 lines Aa and AE.


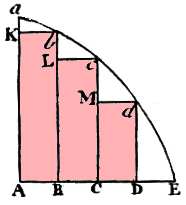
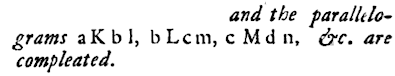

 |
 |
| Lower rectangles | Upper rectangles |
In other words, if we draw more and more thinner rectangles in the same manner, the area of the lower rectangles and the area of the upper rectangles will converge on the area under the curve. This is the area we need to find.
Below is the case where we have 25 rectangles. We can see the total areas of the rectangles is getting close to the area under the curve. Certainly the following ratio approaches 1, as Newton says.
lower rectangles : upper rectangles : area under the curve
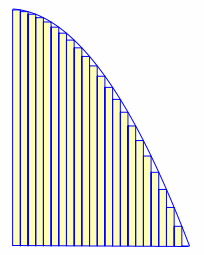 |
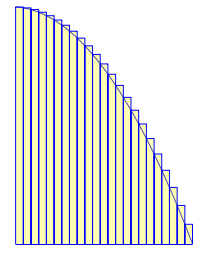 |
| Lower rectangles | Upper rectangles |
This is a fundamental idea of calculus - find an area (or slope) for a small number of cases, increase the number of cases "ad infinitum", and conclude that we are approaching the desired answer.
You can explore this concept further (using an interactive graph) in the article on Riemann Sums.
Archimedes' contribution
This concept of finding areas of curved surfaces using infinite sums was not that new, since Archimedes was aware of it 2000 years ago. (See Archimedes and the Area of a Parabolic Segment.)
Learn math from primary sources
It is very interesting to see Newton's original notation and expression, even if it is via an English translation. The above, of course, is a very small part of Newton's original Principia.
We should learn (and teach) mathematics with a better understanding of why the math was developed, when it was developed and who developed it. We can't always use primary sources, obviously, but it is better to learn math with an understanding of its historical context rather than do it in a vacuum.
See the 28 Comments below.


22 Jul 2010 at 9:03 pm [Comment permalink]
St John's College teaches math this way.
22 Jul 2010 at 10:08 pm [Comment permalink]
St John's College appear to have a clear historical context in their math teaching!
25 Jul 2010 at 1:17 am [Comment permalink]
OH my God.
How nicely and lucidly explained the original theory of Sir Issac Newton.
We would like to read the English translation of Principia,please suggest us.
Thanks.
25 Jul 2010 at 7:51 am [Comment permalink]
Hi Shaikh. Glad you enjoyed the article. There is a link to the English translation in the article, but here it is again for convenience: 1729 English Translation of Principia
10 Jan 2011 at 2:24 am [Comment permalink]
"We should learn (and teach) mathematics with a better understanding of why the math was developed, when it was developed and who developed it. We can’t always use primary sources, obviously, but it is better to learn math with an understanding of its historical context rather than do it in a vacuum."
This is so true. I've had the same issues with the ahistorical instruction of mathematics. Would you know any texts which go through mathematics historically (I mean develop it along its historical course)?
Thanks (and kudos for all this work you've put in),
Haroon
10 Jan 2011 at 1:16 pm [Comment permalink]
Glad you found it useful, Haroon.
Sadly, authors seem to separate textbooks from history of math. An Amazon search didn't find much, but this one looks interesting: Historical Connections in Mathematics: Resources for Using History of Mathematics in the Classroom.
Does anyone know about a good textbook that also includes a lot of historical context?
1 Feb 2011 at 3:13 am [Comment permalink]
Thank YOU and Thank YOU SO MUCH.
10 Mar 2011 at 1:34 am [Comment permalink]
Thanks for the help interpreting the Principia. My son is writing a paper comparing Newton's caluclus method to Leibniz', and we have been trying to figure out if Newton ever performed integration by substitution. He seems to have generally taken the route of converting transcendental functions to polynomials (using infinite series)then using term-wise integration. The question is, was Leibniz alone in coming up with the very powerful tool of using substitution? Certainly, his notation seems more suited for this.
10 Mar 2011 at 2:34 pm [Comment permalink]
@Kathy: I don't profess to be an expert in this area, but I do find it interesting.
It appears unlikely Newton provided a formula for integration by substitution. A history of analysis By Hans Niels Jahnke suggests he would have more likely provided examples of how it could be done. Newton's notation was often quite difficult, of course. Leibniz was much more interested in making readable and meaningful mathematics (as am I!)
If I find more definitive statements on this issue, I'll let you know.
6 Sep 2011 at 11:36 am [Comment permalink]
If you want mathematics taught with a historical backdrop, check out any book by Morris Kline. Full of history, background and application.
His books are downright cheap as textbooks. Seems that since his teaching methods were ditched towards the end of his own life, they have become completely scrapped by academia.
6 Sep 2011 at 8:18 pm [Comment permalink]
Thanks for reminding me of Kline, Aaron. Good tip!
19 Oct 2011 at 1:51 pm [Comment permalink]
I just read through this article and then saw the first comment and had to laugh. I go to St. John's College and was just trying to get some ideas rolling for a paper on Newton's integration. The diagrams of the areas with 25 rectangles are really helpful aides!
3 Mar 2012 at 3:02 pm [Comment permalink]
Simply I feel like listening directly from Sir Isaac Newton about Calculus.
13 Apr 2012 at 5:13 pm [Comment permalink]
I like the part where it's mentioned,"We should learn (and teach) mathematics with a better understanding of why the math was developed, when it was developed and who developed it. We can’t always use primary sources, obviously, but it is better to learn math with an understanding of its historical context rather than do it in a vacuum.",this is really lacking in most places.This would formulate a better understanding of the math.
10 Jun 2012 at 12:55 pm [Comment permalink]
what about differentiation?
10 Jun 2012 at 3:19 pm [Comment permalink]
@Abhishek: This is a good topic for a future article!
Newton used his "method of fluxions" to differentiate. His notation is pretty horrible, and that's why for the most part we use Leibniz's dy/dx notation.
You can see Newton's original (translated to English) here: The Method of Fluxions and Infinite Series/
12 Jun 2012 at 3:00 am [Comment permalink]
Wikipedia often does a good job giving historical background to mathematical concepts.
29 Jun 2012 at 6:13 pm [Comment permalink]
Integration = ?Newton dx
Summation of Newton's Integral !
27 Aug 2012 at 3:46 am [Comment permalink]
Hi,
Newton did not confirm Kepler.In his PRINCIPIA he discovered that the orbit of the planets is spiraled.But this idea was disregarded,even by Newton himself,due to Kepler's orbit theory in trend at that time.He said: orbits can not be spiraled,or parabolic,or hyperbolic.Because on such trajectories the planet will go to "ad infinitum".As they are at our reach for calculation these type of orbits are not valid.But modern "energy conservation equation" gives
r=-4*t^2+4*t*T-4*T^2/6 as the equation of celestial motion.
This equation is the sign of "finitum" distances. Brief:Kepler laws are not correct.Orbits of the planet are spiraled.No ellipse,no aphelion,no perihelion.nor area law.No period understanding as (r) is changing every second.
But a time law r*Vp^2=Ct is valid for the whole solar system at a given era.Try it to believe: get data (r,Vp) of any planet and calculate.Even for Halley and Pluto this constant is valid according Newton's laws.
31 Aug 2012 at 11:15 am [Comment permalink]
@Necat - thanks for your additions!
12 Oct 2012 at 11:01 am [Comment permalink]
Thanks for the help interpreting the Principia.Its really help me thanks again.
6 Jan 2013 at 12:25 pm [Comment permalink]
Thanks for the article! This is very cool. I'm a high school student taking calculus right now and stuff like this makes me remember why I started liking math so much as a young one. I loved learning about the history behind the numbers and this was a great reminder of that! 🙂
10 Jan 2013 at 5:24 pm [Comment permalink]
One has to read Newton's PRINCIPIA translation to English by Andre Motte,page 290,to see his discovery about spiraled orbits and his comments for "ad infinitum" reasoning.The new mathematics is so:Consider Newton's F*dt=m*dv where all componenets are vectorial.Then,Work=F*L is vectorial.With indices (r=radial) and (p=perpandicular) we write Wp=Fp*Lp.
When differentiated dWp=dFp*Lp+Fp*dLp.Considering F*dt=m*dv , that is to write dWp=d(m*dv/dt)*Lp+(m*dv/dt)*dL
From physics we know: no work is done in the direction perpandicular to the attraction field.So, dWp=0 and for this
(m*dv/dt)=0.When integrated v=Constant is found.This means that Kepler's area law (L*Vp=Constant) is not correct.But forcely Newton's Vp=Constant is rigth.This result bring
L=r=-at^2+a*t*T-1/6*aT^2 (where T is the life-time of the celestial body and t is the real time)as the equation of celestial bodies and this equation is an "ad finitum"type equation.This is the point where Newton made a wrong comment about celestial orbits.Celestial spirals do not go on"ad infinitum".But on "ad finitum".For more details,please contact me: [email protected]
10 Jan 2013 at 6:20 pm [Comment permalink]
About integration:
When it is impossible to integrate a function,you have to use Newton's method: that is to get the sum of billions of small terms.Consider dL^2=dx^2+dy^2 and we want L=Sum of dL.It takes too much time to get this SUM.With our modern facilities it takes no time.Use an excell table and just make the sum of dL.The result is quasi-equal to the integral.For exemple "what is the arc length on positive Cartesian of an astroid.We know the astroidal function
(x/a)^r+(y/b)^r=1 (where ,when r=2,we mean an ellipse).By summing, we get the most accurate evaluation.The accuracy depends of the quantity of terms in consideration.When you push the calculation,you find s=r*t/(r-t) and a^s+b^s=L^s.
This is an implicit equation solvable only by SUMMING. Integration is impossible.Solving a^s+b^s=L^s with Newton's method, an accuracy represented by error%=0,000002..was reached in 1959.While in 2009 the error% was=0,000145...with estimation method of math world.Ramanujan's estimations are no more valid.But Thales a^s+b^s=L^s,solved with Newton's summing method,are more accurate. Details:[email protected]
23 Oct 2014 at 12:12 am [Comment permalink]
If you want to understand Isaac Newton, the first rule is on no account should you read Principia. It is a dreadful book. It is better to read the volumes of Newton's works collected by the late Derek Whiteside. The worst part of Principia is the computation and application of the so called inverse square law F = 1/r^2 which is an incorrect upside down version of Kepler's distance law v^2 =1/r which is at last being accepted as applying throughout the whole universe.
24 Oct 2014 at 5:57 pm [Comment permalink]
Hi,
When I read PRINCIPIA by A.Motte page 290,I understood that Newton had a wrong comment on what he discovered about the orbits of celestial body. He said orbits of celestial body should not be parabolic, or hyperbolic, or spiraled. When he said this, he meant an open end orbit. Orbits should be closed. Spiraled orbit also had an open end and the celestial body on this orbit should go ad "infinitum".
No, no. I made the calculation according Newton laws and found that the spiraled orbits have not an open end trajectory but a closed end, an ad "finitum" end. Newton was wrong about his comment of his discovery of the spiraled orbits and accepted unfortunately elliptical orbits. So since 400 years the community is trained on wrong direction. Kepler laws are totally wrong. Elliptical orbit are accepted without prove. Then an area law is pronounced. Kepler says r*Vp=Ct, where (r) is the ray planet-sun and (Vp) is the perpendicular velocity to the attraction direction. Not tangential velocity but perpendicular. Newton laws say the contrary. First Vp=Ct is proved. Vectorial Fattraction is composed of Fattraction=Fr+Fp vectors components. Attraction is radial. Fr exist=m*dVr/dt. A side attraction does not exist. So Fp=0=m*dVp/dt=does not exist. When integrating Vp=Ct is discovered. And when using Vp=Ct in the energy conservation equation, we get r=-4*t^2+4*t*T-4*T^2/6 as the equation of celestial body. This equation is not an ellipse but a parabola on Cartesian, or a closed end spiral on polar. So elliptical orbits should not be accepted without any prove, but proved orbits are spiraled.
Sincerely
[email protected]
26 Nov 2014 at 10:26 am [Comment permalink]
Keplerian estimation for celestial bodies is an unproved physics.Just you must accept that the orbits are elliptical. Then area law is discovered.And r*Vp=Ct is said to be correct.No it is not so.Vp is the perpendicular velocity of the body,Vr is the radial velocity.According Kepler ,when on an elliptical orbit,the velocity of the body change 2 times a year. Getting bigger when coming from aphelion to perihelion,then diminushing when going from perihelion to aphelion.This means that the body has an acceleration on the orbit and we,the human beings,we do not feel this acceleration.Is that possible,for the humanity,not perceiving this acceleration? Yes,because such acceleration does not exist: that the orbital velocity,in the direction perpendicular to the radial attraction direction does not exist,that Vp=Ct.Then r*Vp=Ct is not correct.No area law.Also no period law for Keplerian concept as the velocity on the orbit should stay constant, as explained by Newton mathematics:Period law is valid only and only for circular movement with constant Vp=peripheral velocity.No acceleration.Then Kepler laws are wrong.The correct law is that the orbits are spiraled as Newton has discovered but rejected as seen on page 290 of Andre Motte traduction of PRINCIPIA.
Newton thougth that the end of such a spiraled orbit is not closed,it is going "ad infinitum",like parabolas and hyperbolas of the conical sections.No,no.It is a closed end spiral and it goes ad "finitum".And the celestial movement equation r=*4*t^2+4*t*T-4*T^2/6 does not means an ellipse but a cycloidal spiral with billion of layers. Only one maximum on the orbit and not two maximums ,aphelion and perihelion,for each cycle of the body around the sun.Aphelion and perihelion do not exist.
26 Nov 2014 at 10:47 am [Comment permalink]
A correction is necessary as follows:
Yes,because such acceleration does not exist: that the orbital velocity,in the direction perpendicular to the radial attraction direction does not change,that Vp=Ct.Then r*Vp=Ct is not correct.