Skip to main content
Interactive Mathematics
Search IntMath
Close

Newton’s Method interactive graph

By Murray Bourne, 30 Jul 2015

I added a new interactive graph that helps explain how Newton's Method works. You can find it here:

Go to: Newton's Method Interactive Graph

Newton's Method uses differentiation to solve non-linear equations and is especially useful when we can't factor the equation. It's very commonly used by computers when solving math-based problems.

The graph allows you to explore 4 different functions, and to see what is going on when applying Newton's Method to those functions.

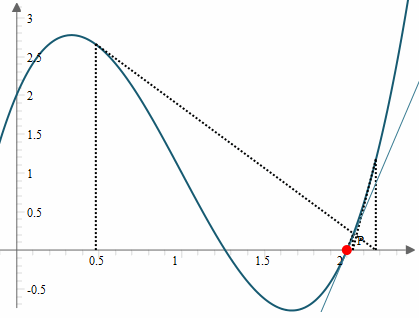
You can see one of the big traps for the unwary. It doesn't always work out that the root you get is the closest one.

For example, the initial guess in this case was x0 = 0.5. The closest root is near x = 1.3, but the actual root found is one near x = 2.

Newton's Method example

Also, strange things can happen if our first guess is too close to a local maximum or minimum. Try it!

Visuals are important

I remember when I first learned Newton's Method. We happily differentiated and substituted. The examples were always "nice" with straightforward solutions. I wasn't really sure what was going on, even though I could apply the algorithm.

A visual representation is very useful for a better understanding of this concept.

See the 2 Comments below.

Related posts:

  1. Intersection of 3 planes at a point: 3D interactive graph This 3D planes applet allows you to explore the concept of geometrically solving 3...
  2. New 3D interactive graph I recently added a 3D interactive graph which you can use to explore the...
  3. Fourier Series interactive graph Here's an interactive graph that allows you to explore the concepts behind the Fourier...
  4. Double springs interactive graph The revised double spring applet now allows exploration on mobile devices. Here is some...
  5. New z-Table interactive graph Investigate the meaning of the z-table using this interactive graph....

Posted in Mathematics category - 30 Jul 2015 [Permalink]

Tags: , ,

2 Comments on “Newton’s Method interactive graph”

  1. Rene Grothmann says:
    25 Aug 2015 at 11:29 pm [Comment permalink]

    I did the demo in EMT on my blog (should be linked). Admittedly, JavaScript is ready everywhere. But the demo looks to closed to me to be of much educational value.

  2. Murray says:
    26 Aug 2015 at 10:40 am [Comment permalink]

    @Rene: Thanks for the information.

    I have a broad range of readers with a broad range of backgrounds and even wider set of "have a go" skills. If the interactive graph requires too much work, most will leave. So the compromise is to provide something that the interested reader can explore and be up and running quite quickly.

    But I agree with you it's probably best to have at least 3 or 4 interactive graphs so readers can find one that suits their level of interest and familiarity with the concept.

    Now, to find 5 more hours a day to implement such a thing...

Leave a comment




Comment Preview

HTML: You can use simple tags like <b>, <a href="...">, etc.

To enter math, you can can either:

  1. Use simple calculator-like input in the following format (surround your math in backticks, or qq on tablet or phone):
    `a^2 = sqrt(b^2 + c^2)`
    (See more on ASCIIMath syntax); or
  2. Use simple LaTeX in the following format. Surround your math with \( and \).
    \( \int g dx = \sqrt{\frac{a}{b}} \)
    (This is standard simple LaTeX.)

NOTE: You can mix both types of math entry in your comment.

top

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.